Обучение в нечетких нейронных сетях для задач управления

На рисунке 2.51 показана схема супервизорного обучения в ННС.

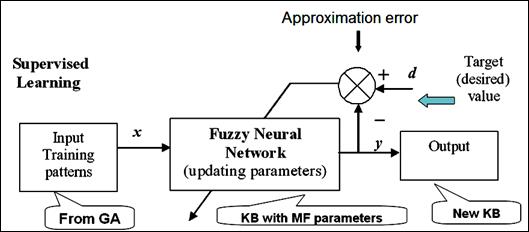
Рис. 2.51. Схема супервизорного обучения в ННС

Задача обучения формулируется следующим образом: на основе обучающей выборки, которую в дальнейшем будем называть «обучающим сигналом» (ОС), настроить параметры сети так, чтобы ошибка аппроксимации ОС была минимальной.

Мера ошибки аппроксимации может быть выбрана, например (смотри (2.23)), как

,

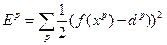где 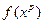– выход ННС, соответствующий выбранной модели нечеткого вывода.

Рассмотрим метод обратного распространения ошибки для ННС, реализующей, например, модель нечеткого вывода Мамдани. В общем виде правила в такой модели выглядят следующим образом:

Правило l:

ЕСЛИ 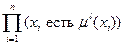ТО ,

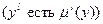где 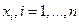– входные лингвистические переменные, « 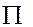» операция нечеткой конъюнкции.

В общем виде, четкое выходное значение в модели Мамдани (с нечеткой конъюнкцией в виде умножения, синглетон-фаззификатором и дефаззификатором «средний максимум») вычисляется по следующей формуле:

,

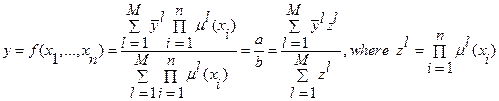где 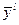- точка максимального значения (центра) функции .

ННС моделирует этот процесс нечеткого вывода с помощью структуры, показанной на рис. 2.51.

Задача обучения в такой сети ставится следующим образом:

С использованием обучающего сигнала настроить параметры сети 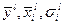так, чтобы мера ошибки аппроксимации была минимальной.

Будем использовать следующее правило обновления параметров сети:

на каждой следующей итерации алгоритма обучения добавлять к параметру 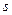его поправку в виде:

,

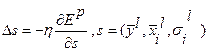где 0 < η < 1 - множитель, задающий скорость обучения.

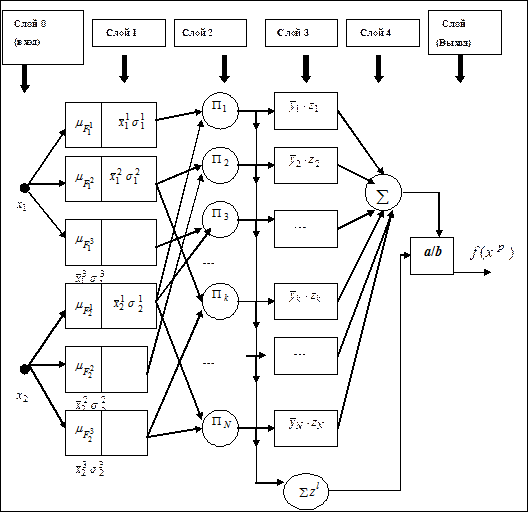
Рис. 2.51. Архитектура ННС для модели нечеткого вывода Мамдани

Вычислим производные функции :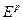

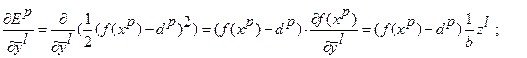
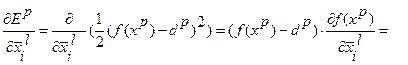
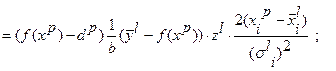
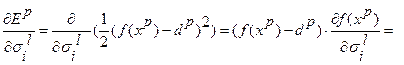
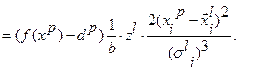
Алгоритм обучения ННС на основе алгоритма обратного распространения ошибки строится следующим образом:

1. Генерируем начальные малые (между 0 и 1) значения параметров сети с помощью генератора случайных чисел или задаем априори. Устанавливаем счетчик шагов обучения 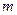= 0; 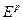= 0. Устанавливаем значение допустимой ошибки .

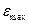2. Устанавливаем счетчик обучающих пар ; .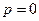

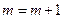3. Если p = P (заданное число обучающих пар), то (если 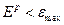, то stop, иначе перейти к шагу 2).

4. p = p +1.

5. Распространяем вход p-ой обучающей пары через сеть и вычисляем результат.

6. Вычисляем общую ошибку

.

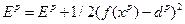7. Обновляем параметры:

;

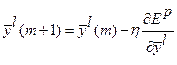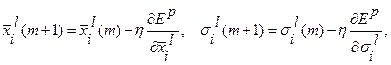
8. Переходим к шагу 3.

Блок-схема данного алгоритма показана на Рис.2.52.

В данной главе мы рассмотрели следующие основные компоненты технологии мягких вычислений:

· Нечеткие системы, используемые для задач нечеткого вывода и управления;

· Генетические алгоритмы – для задач глобальной оптимизации законов управления;

· Нечеткие нейронные сети - для физической реализации законов оптимального управления, а также для реализации обучения и адаптации БЗ.

В следующих главах мы рассмотрим технологию и разработанный инструментарий для проектирования нечетких контроллеров на основе мягких вычислений и рассмотрим примеры их применения.

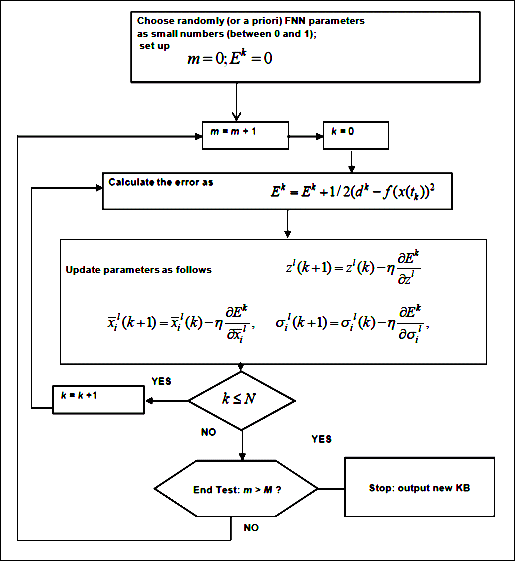
Рис. 2.52. Блок-схема алгоритма обучения ННС на основе алгоритма обратного распространения ошибки

Рекомендуемая дополнительная литература к Главе 2

1. Litvintseva L.V., Ulyanov S.V. Takahashi K., Ulyanov S.S. Intelligent robust control design based on new types of computations. Part 1: New soft computing technology of KB-design Benchmarks of smart control simulation for nonlinear dynamic systems. – Universita degli Studi di Milano, Polo Didattico e di Ricerca di Crema Publ. – 2004. – Vol. 60.

2. Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. – М.: Мир. – 1976.

3. Кофман А. Введение в теорию нечетких множеств. – М.: Радио и связь. – 1982.

4. Tanaka K. An Introduction to Fuzzy Logic for practical Applications. – Berlin: Springer Verlag. – 1991.

5. Алиев Р.А., Ульянов С.В. Нечеткие модели процессов и систем управления. – Итоги Н и Т, Сер. Техническая кибернетика. – 1990. – Т. 29; –1991. – Т. 32.

6. Литвинцева Л.В., Ульянов С.В., Ульянов С.С. Проектирование робастных баз знаний нечетких регуляторов для интеллектуального управления существенно-нелинейными динамическими системами. Ч. II // Изв. РАН. ТиСУ. – 2006. – № 5. – С. 69–97.

7. Holland J.H. Adaptation in Natural and Artificial Systems. – University of Michigan Press, Ann Arbor. – 1975.

8. Goldberg D.E. Genetic Algorithms in Search, Optimization, and Machine Learning. – MA: Addison-Wesley, Reading. – 1989.

9. Емельянов В. В., Курейчик В. В., Курейчик В. М. Теория и практика эволюционного моделирования. — М: Физматлит, 2003. — С. 432.

10. Wasserman P. (1993) Advanced Methods in Neural Computing. Van Nostrand Reinhold, New York.;

11. Kasabov N.K. (1996) Foundations of Neural Networks, Fuzzy Systems, and Knowledge Engineering, MIT Press, Cambridge, Massachusetts

12. Уоссермен, Ф. Нейрокомпьютерная техника: Теория и практика (Neural Computing. Theory and Practice). — М.: Мир, 1992. — 240 с.

13. Hebb D.O. (1949) The Organization of Behavior, New York: Wiley.

14. Patterson D.W. (1996), Artificial neural networks, theory and applications, Prentice Hall, Singapore.

15. Jang J-S.R. , Sun C-T., Mizutani E. (1996) Neuro-Fuzzy Modeling and Soft Computing (A computational approach to learning and machine intelligence), Matlab Curriculum series.

16. Rosenblatt R. (1962) Principles of Neurodynamics, Spartan Books, New York;

17. Minsky M. and Papert S. (1969) Perceptrons: An Introduction to Computational Geometry, MIT Press, Cambridge, Mass.

18. Rumelhart D.E., Hinton G.E.and Williams R.J (1986) Learning representations by backpropagating errors, Nature, Vol.323, 533-536;

19. Freeman J.A. (1994) Back propagation and its variants, Addison-Wesley, Reading, MA.

20. Хайкин, С. Нейронные сети: Полный курс = Neural Networks: A Comprehensive Foundation. — 2-е изд. — М.: «Вильямс», 2006. — 1104 с.

21. Галушкин А. И. Нейронные сети. Основы теории. — М.: Горячая Линия - Телеком. — 2010.

22. Intelligent Quantum & Soft Computing R&D Group [Электронный ресурс] URL: http://www.qcoptimizer.com/ (Дата обращения: 28.04.2011)

Контрольные вопросы к Главе 2

1. Виды искусственных нейронных сетей

2. Нечеткие нейронные сети

3. Процессы обучения и адаптации

4. Структура генетического алгоритма

5. Операторы генетического алгоритма

6. Роль нечетких нейронных сетей и генетического алгоритма в задачах интеллектуального управления