Закон исключенного третьего 7 страница

11.7 Контрольные вопросы и задания

1. Что представляет собой исчисление высказываний?

2. Поясните понятия языка, аксиом и правил вывода исчисления высказываний.

3. Приведите примеры аксиом исчисления высказываний.

4. Каким образом строится дедуктивный вывод?

5. Дайте краткую характеристику основных правил дедуктивного вывода.

6. Перечислите правила дедуктивных выводов логики высказываний.

7. В чем состоит полнота и непротиворечивость исчисления высказываний?

8. Дайте определение независимой системы аксиом.

9. Сформулируйте теорему дедукции.

10. В чем заключается метод доказательства от противного?

Лекция 12. Логика предикатов (логика первого порядка). Предикаты. Алгебра предикатов

12.1 Основные понятия логики предикатов

Логика высказываний, рассмотренная выше, является достаточно узкой логической системой, в ней не все логические рассуждения могут быть осуществлены. Например, в рамках этой системы нельзя записать такое рассуждение «Простое число 2 − четное. Следовательно, существуют простые четные числа».

Многие утверждения, имеющие форму высказываний, на самом деле таковыми не являются, так как содержат переменные, конкретные значения которых не указаны. Поскольку такое утверждение при одних значениях переменных может быть истинным, а при других – ложным, ему не может быть предписано истинностное значение. Такие утверждения называются предикатами. В логику предикатов также введены дополнительные, новые по сравнению с логикой высказываний, логические понятия, а именно, предикат, терм, квантор.

Определение.

Предикатомназывается функция , переменные которой принимают значения из некоторого множества , а сама она принимает два значения (истинное) и (ложное), т.е. (где ).

Понятие предиката является частным случаем понятия функции, для которой четко фиксирована область значений.

Предикаты становятся высказываниями, когда их переменным присваиваются значения.

Пример.

Предикатами являются следующие утверждения: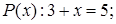

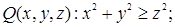
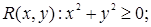
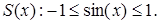
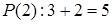Пусть , тогда утверждение является высказыванием, и это высказывание истинно. При 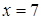утверждение 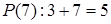тоже является высказыванием, и это высказывание ложно.

Определение.

Множество значений , которое может принимать , называется универсомили предметной областью.

Пример.

В частности, предметной областью может являться множество действительных чисел, множество целых чисел или другие подобные множества.

Множество значений перменных определяется обычно математическим контекстом.

Определение.

В общем случае определен некоторый предикат, если:

1) задано некоторое (произвольное) множество, называемое областью определения предиката (предметная область);

2) фиксировано множество {И, Л}, называемое областью значений;

3) указано правило, с помощью которого каждому элементу, взятому из предметной области, ставится в соответствие один из двух элементов из области значений.

Определение.

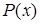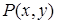Предикат с одной переменной называется одноместным предикатом и может обозначаться, например, , где − переменная. Предикат, имеющий две переменные, называется двухместным предикатом и может обозначаться, например, , где 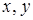− переменные, а предикат, содержащий переменных ( аргументов), называется -местным предикатом и обозначается . Высказывания считаются нульместным предикатом.

Количество аргументов предиката называется его порядком.

Пример.

Высказывание « − действительное число» можно представить одноместным предикатом, « меньше 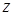» − двуместным предикатом. Есл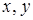и и 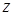замещены конкретными значениями (объектами), то предикат переходит в высказывание, которое рассматривается как нульместный предикат.

Определение.

Аргументы предиката называются термами. Термы-константы и термы-переменные называются предметными константами и предметными переменными.

Предикаты обычно обозначаются большими латинскими буквами. Иногда бывает удобно указывать число переменных у предиката путем введения верхнего индекса, например 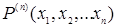является -местным предикатом.

Предикатом чаще всего обозначают свойство или действие, выраженное в высказывании сказуемым, а объекты и субъекты этого действия, а также другие члены предложения являются аргументами данного предиката. В качестве обозначения предиката также можно выбрать слово, отражающее его смысловое значение.

Пример.

Представим в виде предиката высказывания: « делится на 7», « делится на », « − простое число». Выберем в качестве названий предикатов действия или свойства данных предложений: ДЕЛИТСЯ, ПРОСТОЕ. Тогда заданные высказывания можно записать в виде предикатов следующим образом: ДЕЛИТСЯ( ,7), ДЕЛИТСЯ( , ), ПРОСТОЕ( ). Здесь первый и третий предикат являются одноместными и каждый выражает некоторое свойство числа ; второй предикат – двуместный и выражает бинарное отношение делимости на множестве чисел.

Для построения атомов логики предикатов разрешается использовать следующие типы символов:

- индивидуальные символы или константы, которые обычно являются именами объектов, например: Сократ, 13;

- символы предметных переменных, в качестве которых обычно выступают буквы латинского алфавита, возможно, с индексами, например: ;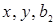

- функциональные символы – строчные буквы латинского алфавита или осмысленные слова из строчных букв, например: минус( 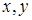) – функциональный символ « 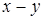», отец ( ) – функциональный символ «отец человека »;

- предикаты– прописные буквы или осмысленные слова из прописных букв, например: , , ДЕЛИТСЯ, БОЛЬШЕ, ПРОСТОЕ.

Пример.

Переведем на естественный язык следующие высказывания логики предикатов: 1) РАВНЯТЬСЯ 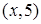; 2) ЗНАТЬ(папа(Вася), математика).

Предикат РАВНЯТЬСЯ 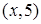соответствует утверждению « равняется 5» естественного языка. Здесь 5 – константа, − предметная переменная.

В высказывании ЗНАТЬ(папа(Вася), математика) функциональный символ «папа( )» принимает значение из множества людей, соответствующее отношению «быть отцом ». Поэтому выражение папа(Вася) следует интерпретировать как «Васин папа». Таким образом, предикат ЗНАТЬ (папа(Вася), математика) соответствует предложению «папа у Васи знает математику» естественного языка. Здесь «Вася» и «математика» являются константами, а − предикатная переменная.

12.2 Операции логики предикатов. Кванторные операции

Над предикатами можно производить обычные логические операции, которые обозначаются символами 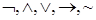и называются логическими связками (как и в логике высказываний).

Пример.

Пусть 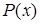− предикат « делится на 3», − предикат « делится на 5», тогда выражение 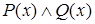означает « делится на 3 и делится на 5», т.е. определяет предикат делимости на 15.

Кроме операций логики высказываний к предикатам применяются операции связывания квантором. Кванторы управляют областью значения переменной, следующей за символом квантора.

Определение.

Пусть 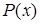− предикат, определенный на множестве . Высказывание «для всех 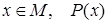истинно» обозначается .

Определение.

Символ называется квантором всеобщности (квантором общности).

Если применяется квантор всеобщности, то говорится, что высказывание истинно для всех из некоторого множества.

Определение.

Высказывание «существует такой 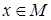, что 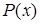истинно» обозначается , где символ называется квантором существования.

Квантор существования применяется, когда нужно указать, что существует хотя бы одно значение переменной, для которой истинно данное высказывание.

Пример.Запишем в виде предикатов с кванторами следующие высказывания: «Все студенты сдают экзамены», «Некоторые студенты сдают экзамены на отлично».

Введем предикаты: − «сдавать экзамены» и − «сдавать экзамены на отлично». Предметная область данных предикатов представляет собой множество студентов. Тогда исходные выражения примут вид: 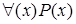и .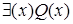

Заметим, что имеют место ранги логических связок, учитывая которые кванторы 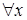и 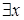размещаются между связкам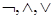и и .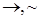

Применение кванторов к многоместным предикатам уменьшает количество переменных, от которых зависит данный предикат. Например, применение квантора по одной из переменных двухместного предиката превращает его в одноместный.

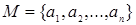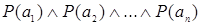Квантор общности можно истолковывать как обобщение конъюнкции, а квантор существования – как обобщение дизъюнкции, т.е. если область определения предиката конечна, например, , то высказывание эквивалентно , а высказывание − дизъюнкции .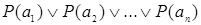

Пример.

Пусть задан предикат 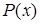, который означает « − нечетное число» и определен на области .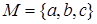

Высказывание 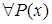означает: « 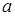− нечетное число», и 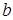− нечетное число и 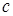− нечетное число», а высказывание 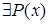означает то же, что и дизъюнкция « 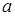− нечетное число, или 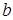− нечетное число, или 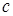нечетное число»

12.3 Формулы и их интерпретация в логике предикатов

На языке предикатов можно составить гораздо более сложные предложения, чем на языке высказываний. Определим понятие формулы в логике предикатов.

Алфавит логики предикатов в общем случае содержит следующие символы:

1) символы предметных переменных: ;

2) символы предикатов: , где ;

3) логические символы: ;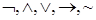

4) символы кванторов: ;

5) скобки и запятую: ),( .

Определение.

Если - -местный предикат и - термы, то называется атомом или элементарной формулойлогики предикатов.

Пример.

Атомами являются: ДЕЛИТСЯ( ,13), ДЕЛИТСЯ( , ), БОЛЬШЕ (плюс( ,1), ), РАВНЯТЬСЯ( ,1), СДАВАТЬ(студенты, сессия).

Определение.

Правильно построенными формулами логики предикатов называются формулы, которые можно рекурсивно определить следующим образом:

1. Атом является формулой.

2. Если и − формулы, то также являются формулами.

3. Если − формула, а − свободная переменная, то и тоже формулы.

4. Никаких формул, кроме порожденных указанными выше правилами, не существует.

Введем понятие свободного и связанного вхождения переменной в формулу.

Определение.

В выражениях и формула 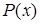, на которую распространяется действие квантора, называется областью действия квантора.

Следует заметить, что формула может и не иметь вхождений переменной . В таком случае считается, что формулы и одинаковые.

Определение.

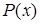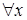Вхождение переменной в формулу называется связанным, если − переменная квантора или 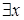, входящего в данную формулу, либо находится в области действия квантора 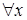или 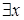, входящего в данную формулу. В противоположном случае вхождение переменной в данную формулу называется свободным.

Пример.

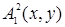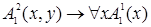Определим вхождение переменных в следующие формулы: а) ; б) , в) .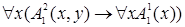

Единственное вхождение переменной в формулу а) является свободным. Первое вхождение переменной в формулу б) свободное, а второе и третье − связанные. Все вхождения переменной в формулу в) связанные.

Определение.

Переход от 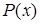к или называется связыванием переменной , а сама переменная в этом случае – связанной. Переменная, не связанная никаким квантором, называется свободной.

Смысл связанных и свободных переменных в предикатных выражениях различен. Свободная переменная − это обычная переменная, которая может принимать различные значения из ; выражение 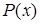– переменное высказывание, зависящее от значения . Выражение не зависит от переменной и при фиксированных и имеет вполне определенное значение. Это в частности означает, что переименование связанной переменной, т.е. 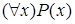переход от к 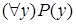, не меняет истинности выражения.

Определение.Формула называется замкнутой, если она не имеет свободных переменных.

Поскольку действие квантора может распространяться не на всю формулу, а только на её часть, то переменная может быть связанной в одной части формулы и свободной в другой. В этом случае полагают, что переменная является и связанной, и свободной одновременно.

Чтобы предикат был высказыванием, все его переменные должны иметь конкретные значения или быть связаны соответствующим квантором.

Пример. 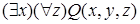не является высказыванием, так как переменная не связана никаким квантором.

Формулы имеют смысл только тогда, когда существует какая-либо интерпретация символов, входящих в эти формулы.

Определение.

Интерпретация формулы логики предикатов состоит из элементов непустой предметной области 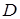, значений всех констант, функциональных символов и предикатов, встречающихся в . Указанные значения задаются следующим образом:

1. Каждой константе ставится в соответствие некоторый элемент из .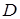

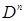2. Каждому -местному функциональному символу ставится в соответствие отображение из в 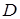. Здесь 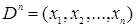, где .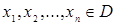

3. Каждому -местному предикату ставится в соответствие отображение из 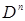в {И, Л}.

Для каждой интерпретации на области 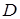формула может получать истинностное значение И или Л согласно следующим правилам:

1. Если заданы значения формул и , то истинностные значения формул ( 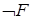), ( ), ( 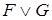),( ),( 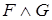) 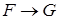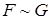получаются с помощью таблиц истинности соответствующих логических операций.