Основні поняття логіки предикатів
Класична математична логіка
Розділ 3
Логіка предикатів першого порядку
Основні поняття логіки предикатів
У розділі 1 формалізація мови у логіці висловлювань здійснюється шляхом розбиття мовних повідомлень на окремі неподільні речення (атоми), а їх змістове об’єднання – за допомогою символів ~ , → ,  ,
, 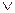 , Ø . Внутрішня структура речень при цьому не враховується. Наприклад, для умовиводу ”Деякі люди геніальні. Сократ ‒ людина. Отже, він геніальний”, інтуїтивно зазначений логічний висновок стосується деяких індивідуумів, до яких Сократ міг і не належати. Тобто в цьому висловлюванні не врахована внутрішня змістова особливість узагальнення
, Ø . Внутрішня структура речень при цьому не враховується. Наприклад, для умовиводу ”Деякі люди геніальні. Сократ ‒ людина. Отже, він геніальний”, інтуїтивно зазначений логічний висновок стосується деяких індивідуумів, до яких Сократ міг і не належати. Тобто в цьому висловлюванні не врахована внутрішня змістова особливість узагальнення
” деякі ”. А якщо розглянути умовивід „Кожна людина смертна. Оскільки Сократ ‒ людина, то він смертний”, то інтуїтивно зазначений логічний висновок є коректним.
Розглянемо цей умовивід більш детально. Для цього введемо атоми: А – ”кожна людина смертна”; В – ”Сократ – людина” ; С – ”Сократ смертний”.
Тоді умовивід відповідатиме формулі логіки висловлювань А  В→ С, або перетворивши яку в нормальну форму, отримаємо
В→ С, або перетворивши яку в нормальну форму, отримаємо
А  В → С =
В → С = 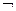 ( А
( А  В )
В ) 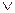 С =
С = 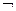 А
А 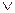
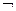 В
В 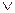 С.
С.
Остання формула на інтерпретації ( I, I, X )хибна, що свідчить про те, що вона не є загальнозначущою. А це означає, що у рамках логіки висловлювань С не є логічним наслідком А і В. Така обмеженість можливостей цієї формалізації пов’язана з тим, що в атомі А не врахована внутрішня змістова особливість узагальнення ”кожний”.
Теорія предикатів ураховує внутрішню структуру речень і ґрунтується на тому, що в цих реченнях подані об’єкти мають певні властивості або знаходяться між собою у певному відношенні. Наприклад, у висловленні
” Сократ – людина ”, підмет ” Сократ ” є об’єктом,а присудок ” людина ” виражає деяку його властивість. Головним для логіки предикатів є саме друга складова речення, що фіксується, а значення об’єкта пропонується позначити деякою змінною величиною. Таким чином, можна розглянути речення ” x – людина ”, яке не є висловлюванням, а є висловлювальною формою, підстановка в яку замість параметра x об’єктів ( значень ) з деякої множини М перетворює форму у висловлювання.
Нехай М – непорожня підмножина декартового добутку M1´M2´…´Mn множин (n ³ 1).
Означення 3.1.1. n - місним предикатом, заданим на множині М, називається речення, що містить n змінних x1,x2,…,xn і стає висловленням при кожній заміні їх елементами з відповідних множин a1,a2,…,an.
n - місний предикат будемо позначати Р(х1, х2,..., xn ), змінні x1,x2,…,xn будемо називати предметними змінними, а елементи множин, які ці змінні приймають (a1,a2,…,an)ϵМ, – предметними константами. Наприклад, над множиною натуральних чисел речення ” х – просте число ” є одномісним предикатом, а речення ” х кохає y ” є двомісний предикат на множині людей.
Таким чином, будь-який n - місний предикат можна ототожнити з логічною функцією n аргументів, що набуває значення із множини {I, X}, тобто
Р ( х  , х
, х  ,... , x
,... , x 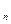 ) : M1´M2´…´Mn → { I,X }.
) : M1´M2´…´Mn → { I,X }.
Це пояснюється тим, що у математичній логіці нас менше цікавить змістова суть предиката, а більш важливо знати, яке значення істинності ставиться у відповідність за допомогою даного предиката тій чи іншій послідовності елементів.
Таким чином, предикат Р( х  , х
, х  ,... , x
,... , x 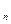 ) буде визначений, якщо: задана деяка множина М, яку називають областю визначення предиката (предметна область); задана область значень (фіксована множина {I,X }); зазначене правило, за допомогою якого кожному елементу, що взятий у предикатній області, ставиться у відповідність один із двох елементів із області значень. Предикат, що не має предметних змінних ( n = 0 ) є висловлюванням або нульмісним предикатом; якщо п = 1, то предикат відповідає властивості; якщо п = 2, то предикат є бінарним відношенням; якщо п = 3, то предикат – тернарне відношення і т. д.
) буде визначений, якщо: задана деяка множина М, яку називають областю визначення предиката (предметна область); задана область значень (фіксована множина {I,X }); зазначене правило, за допомогою якого кожному елементу, що взятий у предикатній області, ставиться у відповідність один із двох елементів із області значень. Предикат, що не має предметних змінних ( n = 0 ) є висловлюванням або нульмісним предикатом; якщо п = 1, то предикат відповідає властивості; якщо п = 2, то предикат є бінарним відношенням; якщо п = 3, то предикат – тернарне відношення і т. д.
Приклад 3.1.1.Подати предикатами речення: ”х – ціле число”; ”х ділиться на у”.
Розв’язання. Дії або властивості цих речень оберемо як назву предикатів: ЦІЛЕ, ДІЛИТЬСЯ. Тоді задані висловлювання можна записати у вигляді предикатів таким чином: ЦІЛЕ(х), ДІЛИТЬСЯ(х, у). Перший предикат є одномісним і виражає деяку властивість чисел, а другий двомісним і виражає бінарне відношення подільності на множині чисел.
Над предикатами можна виконувати звичайні логічні операції. Результатом цих операцій будуть нові предикати. Наприклад, нехай Р( х ) позначає предикат ”х ділиться на 2”, а Q ( x ) ‒ предикат ”х ділиться на 3”. Тоді вираз
Р( х )  Q ( x ) позначає предикат ”х ділиться на 2 та х ділиться на 3”, тобто позначає предикат ”х ділиться на 6”.
Q ( x ) позначає предикат ”х ділиться на 2 та х ділиться на 3”, тобто позначає предикат ”х ділиться на 6”.
За допомогою логічних операцій можна будувати як завгодно складні предикати. Для побудови формул логіки предикатів застосовується алфавіт, у якому є:
предметні змінні x1,x2,…,xn ;
предметні константи a1,a2,…,an ;
функціональні символи fin , де і = 1, 2,… вказує порядковий номер символа, а n = 1, 2,… вказує на кількість аргументів;
предикатні символи Pin , де і = 1, 2,… вказує порядковий номер символа, а n = 0, 1, 2, … вказує на кількість аргу-ментів;
знаки логічних операцій ~ , → ,  ,
, 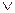 , Ø, ↔; квантори ", $; знаки пунктуації – ліва і права дужки та кома.
, Ø, ↔; квантори ", $; знаки пунктуації – ліва і права дужки та кома.
Серед слів, записаних за допомогою зазначених вище символів, виділяють терми і формули, що визначаються індуктивним чином.
Означення 3.1.2. 1) будь-яка предметна змінна або предметна константа є термом; 2) якщо f – функціональний символ, а 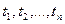 ‒ терми, то f(
‒ терми, то f( 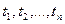 ) є терм; 3) ніяких інших термів, крім породжених за допомогою зазначених вище правил, не існує.
) є терм; 3) ніяких інших термів, крім породжених за допомогою зазначених вище правил, не існує.
Приклад 3.1.2. Записати у вигляді предикатів такі речення: ”Сестра Миколи”, ”Студенти складають іспит”, ”Число х більше числа х - 1”.
Розв’язання 1. Речення ”Сестра Миколи” не може бути ”істинним” або ”хибним”, тому його не можна зобразити у вигляді предиката. Це речення є деяким елементом предметної області на множині людей.
2. Речення ”Студенти складають іспит” може набувати значення ”істина” або ”хибність”, тому його можна записати у вигляді предиката. У структурі речення можна виділити присудок ”складають”, підмет ”студенти” і додаток ”іспит”. Підмет і додаток можна розглядати як
предметні константи, а присудок – як нульмісний предикат. Тому речення ”Студенти складають іспит” можна записати у вигляді нульмісного предиката таким чином: СКЛАДАТИ (студенти, іспит).
3. Присудком у цьому реченні є слово ”більше”. Під-мет ”х” і додаток ”х - 1” зобразимо у вигляді термів. Терм ”х - 1” має внутрішню структуру, оскільки в ньому є функціональний символ ” мінус ”. Виходячи із цього, речення набере вигляду двомісного предиката:
БІЛЬШЕ (( х,1), мінус (х,1)), де х – предметна змінна, а 1 – константа.
Приклад 3.1.3. Предикат ”ДОРІВНЮВАТИ ( х ,7 )” записати природною мовою.
Розв’язання. У предикаті 7 є константа, а х – предметна змінна, тому він відповідає твердженню природної мови –х дорівнює 7.
Квантори
Крім застосування до предикатів ” звичайних ” логічних операцій (~ , → ,  ,
, 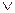 , Ø, ↔) та операції підстановки замість предметних змінних їх конкретних значень, у логіці предикатів використовують так звані операції зв’язування квантором ( операції квантифікації ). Квантори вперше були введені саме в рамках класичної математичної логіки.
, Ø, ↔) та операції підстановки замість предметних змінних їх конкретних значень, у логіці предикатів використовують так звані операції зв’язування квантором ( операції квантифікації ). Квантори вперше були введені саме в рамках класичної математичної логіки.
Означення 3.2.1. Квантором загальностіназивають знак  , під впливом якого предикат Р ( х ) , визначений на множині М, набуває істинного значення для всіх х
, під впливом якого предикат Р ( х ) , визначений на множині М, набуває істинного значення для всіх х 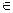 М, і позначають це як
М, і позначають це як  х Р ( х ) .
х Р ( х ) .
Означення 3.2.2. Квантором існування називають знак  , під впливом якого предикат Р (х), визначений на множині М, набуває істинного значення для деяких х
, під впливом якого предикат Р (х), визначений на множині М, набуває істинного значення для деяких х 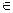 М, і позначають це як
М, і позначають це як  х Р ( х ) .
х Р ( х ) .
Знак квантора загальності  є перевернутою буквою ”А”, що є першою літерою англійського слова ”All”, що означає ” всі ”, а знак квантора існування
є перевернутою буквою ”А”, що є першою літерою англійського слова ”All”, що означає ” всі ”, а знак квантора існування  є перевернутою літерою ”Е”, що є першою буквою англійського слова ” Exist ” і означає ” існування ”. Квантор
є перевернутою літерою ”Е”, що є першою буквою англійського слова ” Exist ” і означає ” існування ”. Квантор  у природній мові читається як ” всі ”, ”кожен”, ”всякий”, ”який би не був”. Квантор
у природній мові читається як ” всі ”, ”кожен”, ”всякий”, ”який би не був”. Квантор  - ”існує (бодай один) ”, ”існують”, ”знайдеться (бодай один) ”, ”знайдуться”, ”деякі”.
- ”існує (бодай один) ”, ”існують”, ”знайдеться (бодай один) ”, ”знайдуться”, ”деякі”.
Якщо квантор застосовується до предиката, то кажуть, що він навішується на формулу.
Наприклад,  х1 Р( х1,x2,…,xn ) – на n - місний предикат навішений квантор загальності, при цьому він зв’язує змінну х1 , а на інші змінні його дія не поширюється. Змінна х1 в цьому разіназивається пов’язаною, всі інші змінні є вільними. Внаслідок операції квантифікації місність предиката зміниться (в цьому випадку предикат стає n-1 - місним).
х1 Р( х1,x2,…,xn ) – на n - місний предикат навішений квантор загальності, при цьому він зв’язує змінну х1 , а на інші змінні його дія не поширюється. Змінна х1 в цьому разіназивається пов’язаною, всі інші змінні є вільними. Внаслідок операції квантифікації місність предиката зміниться (в цьому випадку предикат стає n-1 - місним).
Важливу роль у логіці предикатів відіграє поняття області дії квантора. Область дії квантора – це предикат, на який даний квантор навішується. Як правило, вона виділяється дужками. Наприклад, у предиката
"x $y (x<yÙz>0)↔(x=z) змінна z вільна, змінна x частково вільна, оскільки має два зв’язаних і одне вільне входження, а змінна y пов’язана.
Якщо предикат P(x) не містить інших змінних, крім х, вирази $x P(x) та "x P(x) є реченнями, що виражають істинні або хибні висловлювання.
Приклад 3.2.1. Висловлювання: ” Всі студенти складають іспити ” і ” Деякі студенти складають іспити на відмінно ” подати засобом логіки предикатів.
Розв’язання. Введемо предикати: Р(x) ‒ ” x – складає іспити ”, Q(x) ‒ ” x – складає іспити на відмінно ”, xÎ M, де М – множина студентів. Тоді шукані подання матимуть вигляд  х Р( х ) і
х Р( х ) і  х Q( х ).
х Q( х ).
Приклад 3.2.2. Для предметної області множини дійсних чисел записати засобом логіки предикатів такі твердження: ”Існує число, квадрат якого дорівнює 25”; „ Для всіх х є правильним, що ( х + 2 ) 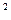 = х
= х 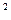 + 4х + 4 ”.
+ 4х + 4 ”.
Розв’язання. Введемо предикат P(х, у) – “ x = y “, який є істинним тоді, коли значення змінної х дорівнює значенню у. У цьому разі, використовуючи квантори, можна записати
 х P( х
х P( х 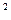 , 25 ) ;
, 25 ) ;  х P( ( х + 2 )
х P( ( х + 2 ) 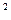 , х
, х 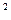 + 4х + 4 ).
+ 4х + 4 ).
Формули логіки предикатів
Означення 3.3.1. Формулою у логіці предикатів називають вираз, який задовольняє такі індуктивні визначення.
1. Якщо P - символ n-місного предиката, а t  ,t
,t  ,...,t
,...,t 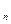 ‒ терми, то Р( t
‒ терми, то Р( t  ,t
,t  ,...,t
,...,t 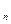 ) ‒ формула, яку називають атомарною( елементарною ). Всі предметні змінні атомарних формул – вільні, пов’язаних змінних немає.
) ‒ формула, яку називають атомарною( елементарною ). Всі предметні змінні атомарних формул – вільні, пов’язаних змінних немає.
2. Якщо P ‒ формула, то 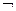 P ‒ також формула. Вільні й пов’язані змінні формули
P ‒ також формула. Вільні й пов’язані змінні формули 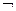 P ‒ це відповідно вільні та пов’язані змінні формули P .
P ‒ це відповідно вільні та пов’язані змінні формули P .
3. Якщо 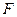 і
і 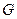 ‒ формули і немає таких предметних змінних, які були б пов’язаними в одній формулі, але вільними в іншій, тоді
‒ формули і немає таких предметних змінних, які були б пов’язаними в одній формулі, але вільними в іншій, тоді 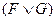 ,
, 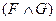 ,
, 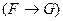 , (
, ( 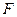 ~
~ 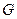 ) є теж формулами, в яких статус змінних зберігається.
) є теж формулами, в яких статус змінних зберігається.
4. Якщо Р ‒ формула, яка містить вільну змінну х, то  x P і
x P і  x P також є формулами. Змінна х у цих формулах стає пов’язаною. Статус інших змінних зберігається.
x P також є формулами. Змінна х у цих формулах стає пов’язаною. Статус інших змінних зберігається.
5. Ніяких інших формул, крім породжених зазначеними вище правилами, не існує.
Приклад 3.3.1. Визначити, які із виразів є формулами логіки предикатів:
а) P ( x  ,x
,x 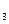 ,x
,x 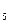 ) ;
) ;
б)  x1
x1  x2 P ( x1,x2,x3 )
x2 P ( x1,x2,x3 ) 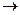
 x1P ( x1,x4);.
x1P ( x1,x4);.
в)  x1
x1  x3 ( P ( x1, x3 )
x3 ( P ( x1, x3 )  P ( x3, x4 ).
P ( x3, x4 ).
Розв’язання. Вираз а) є атомарною формулою, в якій x  ,x
,x 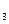 ,x
,x 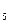 ‒ вільні змінні. Вираз б) є формулою, в якій x
‒ вільні змінні. Вираз б) є формулою, в якій x  ,x
,x  ‒ пов’язані змінні, а x
‒ пов’язані змінні, а x 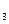 , x
, x 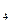 ‒ вільні змінні.
‒ вільні змінні.
Вираз в) не є формулою, оскільки порушене правило 3 означення 3.3.1.
Приклад 3.3.2. Визначити, які змінні є пов’язаними, а які вільними у таких формулах:
г) Р( х,у,z ),;  y ( P( x )
y ( P( x ) 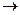
 x Q( x,y )) ;
x Q( x,y )) ;  y ( P( y )
y ( P( y ) 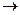
 y Q( x,y )) .
y Q( x,y )) .
Розв’язання. Усі три змінні у формулі а) є вільними. У формулі б) змінна у є пов’язаною, а змінна x – і пов’язаною, і вільною. У формулі в) змінна х є вільною, а змінна у пов’язаною.
Означення 3.3.3. Інтерпретацією формули логіки предикатів називається система, що складається з непорожньої множини М Ì (М1´М2´…´Мn), яку називають областю інтерпретації, і відповідності, яка кожному предикатному символу Pin зіставляє певний n - місний предикат, заданий на множині М, кожному функціональному символу fin – деяку n - арну алгебраїчну операцію, кожній константі αi – деякий конкретний елемент із М.
Для кожної інтерпретації на області 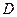 формула F може набувати істинного І, або хибного Х значення згідно з такими правилами.
формула F може набувати істинного І, або хибного Х значення згідно з такими правилами.
1. Якщо задані значення формул F і G, то значень істинності формул 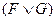 ,
, 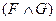 ,
, 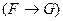 , (
, ( 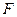 ~
~ 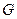 ) можна визначити за допомогою таблиць істинності відповідних логічних операцій.
) можна визначити за допомогою таблиць істинності відповідних логічних операцій.
2. Формула  x F набуває значення І, якщо F набуває значення І для кожного х із предикатної області
x F набуває значення І, якщо F набуває значення І для кожного х із предикатної області 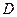 , у протилежному разі ‒ Х.
, у протилежному разі ‒ Х.
3. Формула  x F набуває значення І, якщо F набуває значення І для деякого х із предикатної області
x F набуває значення І, якщо F набуває значення І для деякого х із предикатної області 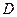 , у протилежному разі ‒ Х.
, у протилежному разі ‒ Х.
Означення 3.3.4.Формула логіки предикатів називається :
a) істинною в даній інтерпретації, якщо вона виконується на будь-якому наборі елементів з області інтерпретації;
b) хибною в даній інтерпретації, якщо вона не виконується на жодному наборі елементів з області інтерпретації;
c) виконуваною в даній інтерпретації, якщо вона виконується хоча б на одному наборі елементів з області інтерпретації;
d) спростовною в даній інтерпретації, якщо вона не виконується хоча б на одному наборі елементів з області інтерпретації.
Приклад3.3.3.Побудувати інтерпретацію формул: P( x  ,x
,x  ) ;
) ;  x
x  P( x
P( x  ,x
,x  ) ;
) ;  х2
х2  х1 Р( х
х1 Р( х  , х
, х  ).
).
Розв’язання. Введемо область інтерпретації – множину цілих додатних чисел Z+ , а замість P(x1, x2) введемо предикат ”x1 ≥ x2 ”. Перша формула – це саме предикат, побудований на Z+. Вона є виконуваною і спростовною. Друга формула буде виражати одномісний предикат, вона є хибною. Третя формула – це істинне висловлювання, яке стверджує про існування найменшого цілого додатного числа.
