Домашняя самостоятельная работа №4

Задание:подготовка краткого конспекта теоретического вопроса «Модальные суждения».

Требования к оформлению:не более 2 печатных листов (14 кегль, 1,5 интервал), указание на используемую литературу и интернет - ресурсы.

Примечание: максимальная оценка - 5 баллов, необходимо набрать не менее 3 баллов.

Тема 4 (продолжение)

Информационный материал

Сложные суждения образуются из простых, а так же из других ложных суждений помощью логических союзов «если … то….», «или», «и» и т. д., с поощью отрицания «неверно, что…», модальных терминов «возможно, что..», «необходимо, что…», «случайно, что…», и т. д.

Соединительные суждения – это суждения, в которых утверждается наличие двух и более ситуаций. Чаще всего такие суждения выражаются посредством предложений, содержащих союз «и». Встречающийся в естественном языке союз «и» употребляется в нескольких значениях. В логике употребляется союз «и», имеющий определенный смысл. Этот союз обозначается символом 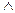(читается «и»), называемый знаком конъюнкции. Суждение с этим союзом называется конъюнктивным. Определением знака конъюнкции является таблица показывающая зависимость истинности конъюнктивного суждения от истинности составляющих его суждений.

Форма конъюнктивного суждения: ( 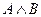). Каждое из высказываний А и В может принимать как значение «истина», так и значение «ложь». Эти значения для краткости будем обозначать «и», «л» («1» или «0»). Таблица истинности для соединительного суждения имеет вид:

А	В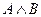

Разделительные суждения – это суждения, в которых утверждается наличие одной из двух, трех и более ситуаций. Если утверждается наличие по крайней мере одной из двух ситуаций, суждение называется нестрого разделительным, или дизъюнктивным. Если утверждается наличие ровно одной из двух или более ситуаций, то суждение называется строго-разделительным или строго-дизъюнктивным. Чаще всего утверждения первого типа реализуются посредством предложений с союзом «или, «либо», а второго - с союзом «или, …или», «либо, .. либо». Союз «или», посредством которого выражается утверждение первого типа, обозначается символом (читается «или»), называемым знаком нестрогой дизъюнкции (или просто знаком дизъюнкции), а союз «или, … или», посредством которого выражается утверждение второго типа, - символом (читается «или, … или»), называемым знаком нестрогой дизъюнкции.

Табличные определения знаков нестрогой и строгой дизъюнкции имеют вид:

А	В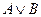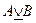

Примерами нестрого- и строго-дизъюнктивного суждения могут служить следующие сложные суждения: «Иванов является юристом или Иванов является спортсменом», «Либо Иванов совершил это преступление, либо Иванов не совершал этого преступления».

Символ 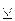(в другой терминологии 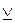₂) – это знак двухместной строгой дизъюнкции. Знак трехместной строгой дизъюнкции - 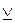₃ (читается «или…, ил…, или…») определяется посредством следующей таблицы:

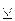А	В	С	3 (а, В, с)

Пример суждения этого вида: «Или Иванов совершил это преступление, или Петров, или Сидоров».

Условные или импликативные суждения. Суждения, в которых утверждается, что наличие одной ситуации обуславливает наличие другой, называется условным. Условные суждения чаще всего выражаются предложениями союзом «если.., то …».

В условном суждении выделяют основание и следствие. Основанием (антецендентом) называется та часть условного суждения, которая располагается между словом «если» и словом «то». Часть условного суждения, которая находится после слова «то», называется следствием (консеквентом).

Условный союз «если…, то …» обозначается знаком «→».

В построениях современной логики находит широкое распространение союз «если.., то …», обозначаемый символом « 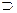». Этот символ называется знаком (материальной) импликации, а суждение с этим союзом - импликативным. Знак импликации определяется следующей таблицей истинности:

А	В

Суждения эквивалентности и материальной эквивалентности. Суждения эквивалентности – это суждения, в которых утверждается взаимная обусловленность двух ситуаций. Суждения эквивалентности выражаются, как правило, посредством предложений с союзами «если и только если, то…», «тогда п и только тогда, когда… », «необходимо и достаточно». Союз «если и только если, то… », употребляемый в описанном смысле, обозначается символом «↔».

Союз «если и только если, то… » употребляется еще в одном смысле. В этом случае он обозначается символом « 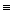», называемым знаком материальной эквивалентности, который определяется следующей таблицей истинности:

А	В

Суждения с этим союзом называются суждениями материальной эквивалентности.

Суждения с внешним отрицанием – это суждения, в которых утверждается отсутствие некоторой ситуации. Оно чаще всего выражается предложением, начинающимся словосочетанием «неверно, что». Внешнее отрицание обозначается знаками «», « 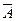», « », 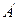называемыми знаками внешнего отрицания. Этот знак определяется следующей таблицей истинности: