Закон исключенного третьего 2 страница
Теорема о конъюнктивном разложении булевой функции 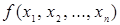 по
по  переменным.
переменным.
Любую булеву функцию 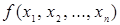 можно представить в следующей форме
можно представить в следующей форме 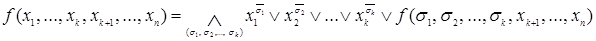 .
.
Запись 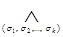 означает многократную конъюнкцию, которая берется по всем возможным наборам значений
означает многократную конъюнкцию, которая берется по всем возможным наборам значений 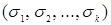 при любом
при любом 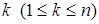 .
.
Следствие 3. Конъюнктивное разложение булевой функции 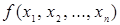 по одной переменной.
по одной переменной.
Любую булеву функцию 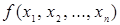 можно представить в следующей форме
можно представить в следующей форме 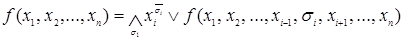 .
.
Запись 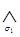 означает, что конъюнкция берется по всем значениям
означает, что конъюнкция берется по всем значениям 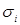 , то есть по 0 и по 1. Запись
, то есть по 0 и по 1. Запись 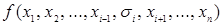 обозначает значение функции на наборе
обозначает значение функции на наборе 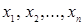 , где вместо значения переменной
, где вместо значения переменной 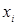 подставлено
подставлено 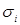 .
.
Следствие 4. Конъюнктивное разложение булевой функции 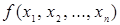 по всем
по всем  переменным.
переменным.
Любую булеву функцию 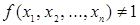 можно представить в следующей форме:
можно представить в следующей форме: 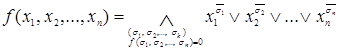 .
.
Запись 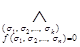 означает, что конъюнкция берется по всем наборам значений
означает, что конъюнкция берется по всем наборам значений 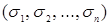 , на которых
, на которых 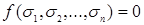 .
.
Пример.
Запишем конъюнктивное разложение функции 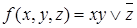 по всем переменным. Определим значение функции на каждой интерпретации:
по всем переменным. Определим значение функции на каждой интерпретации:
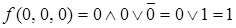 ,
, 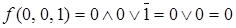 ,
,
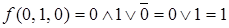 ,
, 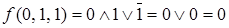 ,
,
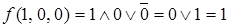 ,
, 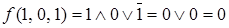 ,
,
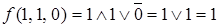 ,
, 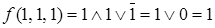 .
.
Запишем формулу, используя следствие 4 теоремы о разложении функций
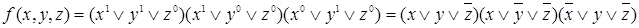
СКНФ функции является результатом конъюнктивного разложения функции по всем переменным.
7.4 Переход от табличного представления функции к алгебраическому представлению функции
Любая таблично заданная функция алгебры логики может быть представлена в виде 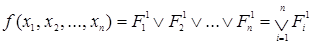 или в виде
или в виде 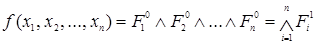 ,
,
где 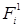 - элементарная конъюнкция ранга
- элементарная конъюнкция ранга  (конституента единицы);
(конституента единицы);
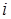 - номера наборов, на которых функция
- номера наборов, на которых функция 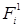 равна 1, а функция
равна 1, а функция 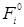 равна 0;
равна 0;
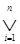 - символ обобщенной дизъюнкции;
- символ обобщенной дизъюнкции;
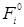 - элементарная дизъюнкция ранга
- элементарная дизъюнкция ранга  (конституента нуля);
(конституента нуля);
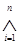 - символ обобщенной конъюнкции.
- символ обобщенной конъюнкции.
Для перехода от таблицы истинности булевой функции к СДНФ можно воспользоваться следующим алгоритмом:
а) выделить в таблице истинности все интерпретации, на которых значение функции равно единице;
б) записать конституенты единицы, соответствующие отмеченным интерпретациям;
в) получить СДНФ функции посредством соединения операцией дизъюнкции записанных конституент единицы.
Пример.
Получим СДНФ для функции 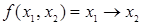 .
.
Используем алгоритм перехода от таблицы истинности к алгебраическому представлению функции.
а) построим таблицу истинности функции и отметим интерпретации, на которых функция равна единице (табл. 7.2).
Таблица 7.2 - Функция 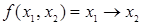 , заданная в табличном виде
, заданная в табличном виде
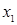 | 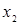 | 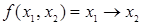 |
б) запишем конституенты единицы, соответствующие отмеченным интерпретациям: 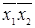 ,
, 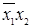 ,
, 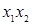 .
.
в) получим СДНФ функции 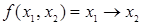 посредством соединения операцией дизъюнкции записанных конституент единицы
посредством соединения операцией дизъюнкции записанных конституент единицы 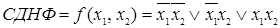
Для перехода от таблицы истинности булевой функции к СКНФ можно воспользоваться следующим алгоритмом:
а) выделить в таблице истинности все интерпретации, на которых значение функции равно нулю;
б) записать конституенты нуля, соответствующие отмеченным интерпретациям;
в) получить СКНФ функции посредством соединения операцией конъюнкции записанных конституент нуля.
Пример.
Получить СКНФ для функции 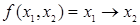 .
.
Используем алгоритм перехода от таблицы истинности к алгебраическому представлению функции.
а) построим таблицу истинности функции и отметим интерпретации, на которых функция равна нулю (табл. 7.3).
Таблица 7.3 - Функция 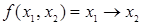 , заданная в табличном виде
, заданная в табличном виде
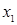 | 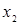 | 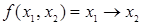 |
б) запишем конституенту нуля, соответствующую отмеченной интерпретации: 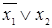 .
.
в) получим СКНФ функции: 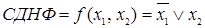 .
.
Обратный переход от алгебраического к табличному представлению функции выполняется путем последовательной подстановки в данное алгебраическое выражение всех возможных наборов переменных, определения соответствующих значений 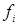 для каждого
для каждого 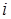 -го набора и заполнения таблиц истинности.
-го набора и заполнения таблиц истинности.
7.5 Правила преобразования произвольной формулы алгебры логики в нормальную форму с использованием законов булевой алгебры
Для любой формулы алгебры логики путем равносильных (тождественных) преобразований можно получить её нормальную форму, причем не единственную.
Рассмотрим правила преобразования произвольной формулы алгебры логики к ДНФ (КНФ) и СДНФ (СКНФ), представленные в виде следующего алгоритма:
1. Исключить константы, используя законы действия с константами.
2. Опустить знаки отрицания непосредственно на переменные, используя законы де Моргана.
3. Используя дистрибутивный закон, раскрыть скобки (для получения КНФ - используя дистрибутивный закон привести функцию к виду конъюнкции элементарных дизъюнкций). К полученным элементарным конъюнкциям (дизъюнкциям) применить законы идемпотентности и противоречия (для получения КНФ - идемпотентности и исключенного третьего), упростить их и привести подобные. Результатом выполнения указанных действий является получение ДНФ (КНФ) булевой функции.
4. Построить конституенты единицы (нуля) введением в каждую элементарную конъюнкцию (дизъюнкцию) недостающих переменных, используя закон исключенного третьего (для получения СКНФ - закон противоречия).
5. С помощью дистрибутивного закона раскрыть скобки и привести подобные (для получения СКНФ - используя дистрибутивный закон привести функцию к виду конъюнкции конституент нуля и упростить формулу), используя закон идемпотентности. Полученная формула соответствует СДНФ (СКНФ) функции.
Пример.
Построим СДНФ функции 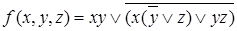 .
.
Воспользуемся правилами преобразования произвольной формулы алгебры логики к СДНФ. Опускаем отрицания на переменные, используя закон де Моргана:
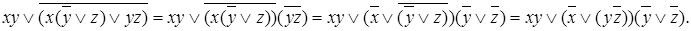 Построим ДНФ, используя дистрибутивный закон, законы идемпотентности и противоречия:
Построим ДНФ, используя дистрибутивный закон, законы идемпотентности и противоречия:
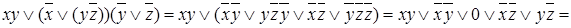
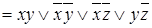 .
.
Так как функция зависит от трех переменных, то в элементарные конъюнкции необходимо ввести недостающие переменные, используя закон исключенного третьего: 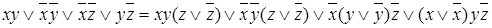 .
.
Используя дистрибутивный закон, раскроем скобки и приведем подобные для получения СДНФ:
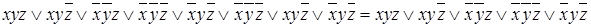 .
.
Получена СДНФ заданной функции:
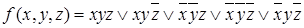 .
.
7.6 Контрольные вопросы и задания
1. На примере булевых функций опишите понятие «нормальной формы» функции.
2. Что представляет собой элементарная конъюнкция, элементарная дизъюнкция?
3. Какая формула называется дизъюнктивной нормальной формой, конъюнктивной нормальной формой?
4. Дайте определение понятиям минтерм, макстерм, конституанта единицы, конституанта нуля.
5. Что такое совершенная нормальная форма и какими свойствами она обладает?
6. Сколько имеется различных конституент единицы и нуля для функции  переменных
переменных 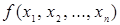 ?
?
7. Сколько ДНФ и сколько СДНФ может иметь булева функция?
8. Запишите формулы дизъюнктивного разложения булевых функций от  переменных по
переменных по 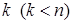 переменным, по всем
переменным, по всем  переменным, по одной переменной.
переменным, по одной переменной.
9. Запишите формулы конъюнктивного разложения булевых функций от  переменных по
переменных по 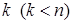 переменным, по всем
переменным, по всем  переменным, по одной переменной.
переменным, по одной переменной.
10. Опишите алгоритмы перехода от таблицы истинности булевой функции к СДНФ и СКНФ.
11. Сформулируйте правила преобразования произвольной формулы алгебры логики в нормальную форму с использованием законов булевой алгебры.
Лекция 8. Минимизация булевых функций
8.1 Основные понятия минимизации булевых функций. Критерии минимизации.
Функция алгебры логики может быть представлена различными формулами (в частности, различными ДНФ и КНФ), а, следовательно, практически может быть реализована различными эквивалентными функциональными схемами.
Пример.
Функция 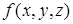 , заданная вектором
, заданная вектором 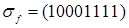 , может быть представлена в виде СДНФ
, может быть представлена в виде СДНФ 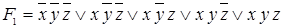 и реализована при помощи соответствующих логических элементов. С другой стороны, эта функция может быть представлена другой ДНФ
и реализована при помощи соответствующих логических элементов. С другой стороны, эта функция может быть представлена другой ДНФ 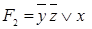 с меньшим количеством букв и символов логических операций, а, следовательно, реализована другой логической схемой.
с меньшим количеством букв и символов логических операций, а, следовательно, реализована другой логической схемой.
При решении практических задач из множества эквивалентных схем можно (и необходимо) выделить (синтезировать) наиболее экономичную или хотя бы достаточно простую схему, которая реализует рассматриваемую булеву функцию в некотором базисе. Данный базис обусловлен имеющимся в распоряжении проектировщика набором логических элементов или выбирается по соображениям наибольшей простоты реализации данного класса функций. Чаще всего задачу синтеза схем связывают с базисом, состоящим из отрицания, дизъюнкции и конъюнкции, который будем называть булевым базисом.
Пример.
Функция 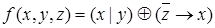 в булевом базисе преобразуется к виду:
в булевом базисе преобразуется к виду:
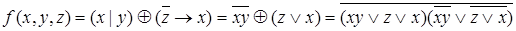 .
.
Если в качестве базиса приняты отрицание и импликация, то функция будет иметь вид 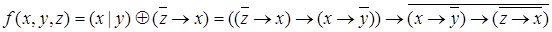 .
.
Для оценки формы булевой функции, которая наиболее предпочтительна для практической реализации, обычно вводится индекс (коэффициент) простоты 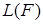 , где
, где  - формула, реализующая функцию, характеризующий «сложность» ДНФ (КНФ). Наиболее часто встречаются следующие виды коэффициентов простоты:
- формула, реализующая функцию, характеризующий «сложность» ДНФ (КНФ). Наиболее часто встречаются следующие виды коэффициентов простоты:
а) 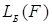 - число символов (букв) переменных, встречающихся в записи ДНФ (КНФ);
- число символов (букв) переменных, встречающихся в записи ДНФ (КНФ);
б) 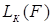 - число элементарных конъюнкций (дизъюнкций), входящих в
- число элементарных конъюнкций (дизъюнкций), входящих в  ;
;
в) 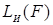 - число символов инверсий, встречающихся в записи ДНФ (КНФ).
- число символов инверсий, встречающихся в записи ДНФ (КНФ).
Пример.
Сравним две формулы 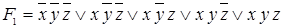 и
и 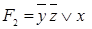 , реализующие одну функцию. Для них:
, реализующие одну функцию. Для них: 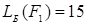 и
и 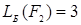 , следовательно
, следовательно 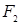 проще, чем
проще, чем 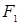 ;
; 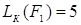 и
и 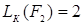 , следовательно,
, следовательно, 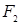 проще, чем
проще, чем 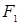 ;
; 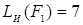 и
и 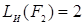 , следовательно,
, следовательно, 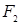 проще, чем
проще, чем 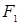 .
.
8.2 Основные определения, используемые при минимизации булевых функций
Рассмотрим некоторые определения, используемые при минимизации булевых функций.
Определение.
Импликантой некоторой функции  называется функция
называется функция 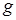 , такая, что на всех интерпретациях, на которых
, такая, что на всех интерпретациях, на которых 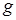 равна единице,
равна единице,  тоже равна единице.
тоже равна единице.
Минтермы любого ранга, входящие в состав ДНФ функции, являются её импликантами.
Определение.
Множество  , состоящее из импликант функции
, состоящее из импликант функции  , называется покрытием (или полной системой импликант) функции
, называется покрытием (или полной системой импликант) функции  , если каждое единичное значение функции
, если каждое единичное значение функции  покрывается единицей хотя бы одной импликанты из множества
покрывается единицей хотя бы одной импликанты из множества  .
.
Пример.
Набор импликант, составляющих ДНФ функции, является её покрытием. Набор всех конституент единицы функции, входящих в её СДНФ, является покрытием данной функции.
Всякая элементарная конъюнкция  , входящая в состав элементарной конъюнкции
, входящая в состав элементарной конъюнкции  и содержащая меньше переменных, чем конъюнкция
и содержащая меньше переменных, чем конъюнкция  , называется собственной частью конъюнкции
, называется собственной частью конъюнкции  , и говорят, что конъюнкция
, и говорят, что конъюнкция  покрывает конъюнкцию
покрывает конъюнкцию  .
.
Определение.
Простой импликантой функции  называется такая конъюнкция-импликанта, что никакая её собственная часть не является импликантой данной функции.
называется такая конъюнкция-импликанта, что никакая её собственная часть не является импликантой данной функции.
Множество всех простых импликант функции составляет покрытие данной функции.
Определение.
Дизъюнкция всех простых импликант функции называется её сокращенной ДНФ.
Определение.
Дизъюнктивным ядром булевой функции  называется такое множество её простых импликант, которое образует покрытие
называется такое множество её простых импликант, которое образует покрытие  , но после удаления импликанты теряет это свойство, то есть перестает быть полной системой импликант.
, но после удаления импликанты теряет это свойство, то есть перестает быть полной системой импликант.
Определение.
Тупиковой ДНФ называется ДНФ данной булевой функции, состоящая только из простых импликант.
В отличие от сокращенной ДНФ, тупиковая ДНФ может не содержать некоторые из простых импликант функции. Каждая булева функция имеет единственную сокращенную ДНФ и может иметь несколько тупиковых ДНФ. В каждую из тупиковых ДНФ входят все импликанты дизъюнктивного ядра данной функции. |Тупиковые ДНФ могут иметь различную сложность и отличаться от минимальных. Среди тупиковых ДНФ всегда содержатся и минимальные ДНФ.
Определение.
Минимальной ДНФ (МДНФ) булевой функции называется одна из её тупиковых ДНФ, которой соответствует наименьшее значение критерия минимизации (индекса простоты) ДНФ.
Пример.
Пусть имеется функция  , заданная в виде СДНФ:
, заданная в виде СДНФ:
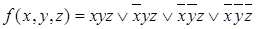 .
.
Выполним операции полного склеивания следующим образом:
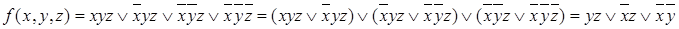 Операцию склеивания можно выполнить другим способом:
Операцию склеивания можно выполнить другим способом:
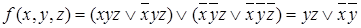 .
.
В обоих случаях получены тупиковые ДНФ функции 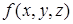 . Вторая тупиковая ДКФ проще первой, поскольку содержит меньшее количество символов переменных и знаков операций.
. Вторая тупиковая ДКФ проще первой, поскольку содержит меньшее количество символов переменных и знаков операций.
Для анализа различных представлений булевой функции через КНФ и получения минимальных КНФ (МКНФ) необходимо использовать принцип двойственности. Двойственные понятия соответственно называются терминами: имплицента, простая имплицента, полная система имплицент, сокращенная КНФ, тупиковая КНФ, минимальная КНФ.
Проблема синтеза логических схем в булевом базисе связана с задачей минимизации булевых функций, которая в общем случае имеет две постановки:
- в аналитической форме;
- в геометрической форме (задача о покрытии).
Употребляются два языка: аналитический и геометрический.
Для решения данной задачи в современной теории и практике алгебры логики существуют следующие основные подходы:
- перебор (просмотр) всех возможных ДНФ и КНФ произвольной функции с целью поиска минимальной формы (первый подход);
- упрощение конкретной функции, достигаемое путем различных тождественных преобразований, с целью получения формулы, эквивалентной исходной, но реализуемой проще (второй подход).
Процесс перебора всех возможных ДНФ и КНФ функции является, хотя и наиболее понятным, но достаточно трудоемким процессом. Им нельзя воспользоваться практически уже с 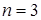 , а для
, а для 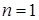 и
и 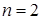 проблема является тривиальной.
проблема является тривиальной.
Процесс поиска минимальных форм становится более наглядным и целеустремленным, если использовать второй подход, т.е. некоторые аналитические и графические представления и специально разработанную для этой цели символику.
В общем случае минимальные формы булевых функций аналитически получают в такой последовательности:
- получают и анализируют конкретную функцию алгебры логики, определенную для всевозможных наборов значений аргументов;
- полученную функцию представляют через основные операции в любой из двух совершенных нормальных форм (СДНФ или СКНФ);
- находят сокращенную ДНФ (КНФ) (любая функция имеет одну такую форму);
- находят возможные тупиковые ДНФ (КНФ);
- из полученных тупиковых форм выбирают минимальные ДНФ (КНФ).
Для нахождения упрощенного аналитического выражения используются следующие очевидные преобразования формул булевой алгебры, которые традиционно называются «операциями».
Рассмотрим данные операции, принимая следующие обозначения:  - некоторая элементарная конъюнкция переменных;
- некоторая элементарная конъюнкция переменных; 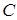 - некоторая элементарная дизъюнкция переменных;
- некоторая элементарная дизъюнкция переменных;  - булева переменная.
- булева переменная.
Операция неполного дизъюнктивного склеивания:
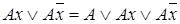 .
.
Операция дизъюнктивного поглощения:
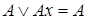 .
.
Выполнение двух указанных операций последовательно представляет собой выполнение операции полного дизъюнктивного склеивания:
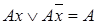 .
.
Операция неполного конъюнктивного склеивания:
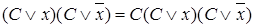 .
.
Операция конъюнктивного поглощения:
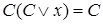 .
.
Операция полного конъюнктивного склеивания:
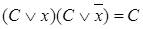 .
.
8.3 Основные методы минимизации булевых функций. Метод минимизирующих карт (диаграммы Карно-Вейча)
Существует несколько известных аналитических и геометрических методов получения минимальных ДНФ (КНФ): метод Квайна−Мак-Класки, метод Порецкого-Блейка, метод минимизирующих карт (диаграммы Карно-Вейча), метод многомерных кубов и др.
Целью минимизации является нахождение минимальной из тупиковых ДНФ (КНФ), т.е. нахождение минимального покрытия данной функции. Для этого необходимо построить все возможные тупиковые ДНФ (КНФ), используя операции склеивания и поглощения для данной функции. Методика использования минимизирующих карт (методика диаграмм Карно и Вейча) позволяет выполнить указанные операции графически. Диаграммы Карно-Вейча представляют собой развертки кубов на плоскости.
Карты Карно (диаграммы Вейча) представляют собой специально организованные таблицы соответствия (истинности). Значения не более двух переменных располагаются в заголовках строк и столбцов карты в таком порядке, что каждый последующий отличается от предыдущего значением только одной из переменных, например, (0, 0), (0, 1), (1, 1), (1, 0). Клетки, расположенные по краям таблицы, считаются соседними и обладают этим свойством.
