Предваренная нормальная форма

Формула в логике первого порядка находится в предваренной нормальной форме (ПНФ) тогда и только тогда, когда она может быть представлена в виде , где каждое , , есть или , или , а − формула, не содержащая кванторов. Причем называется префиксом, а − матрицей формулы .

Предикат

Функция , переменные которой принимают значения из некоторого множества , а сама она принимает два значения (истинное) и (ложное), т.е. (где ).

Предметная константа

Терм-константа называется предметной константой.

То же, что и индивидуальный символ.

Предметная область

Множество значений , которое может принимать в предикате .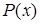

То же, что область определения предикатаилиуниверс.

Предметная переменная

Терм-переменная называется предметной переменной.

Пропозициональная переменная

То же, что и высказывательная переменная.

Противоречивая формула

Формула, которая принимает значение «ложь» на всех интерпретациях.

То же, что и тождественно ложная формулаилиневыполнимая формула.

Равносильность

Отношение эквивалентности (оно рефлексивно, симметрично и транзитивно). То же, что и логическая эквивалентность.

Равносильные формулы

Формулы, которые на всех наборах значений входящих в них переменных принимают одинаковые значения.

Свободная переменная

Переменная в предикатной формуле, не связанная никаким квантором.

Связанная переменная

Переход от 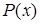к или называется связыванием переменной , а сама переменная в этом случае – связанной.

Следствие

В импликации 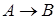высказывание называется следствием.

То же, что и заключение, консеквент.

Тавтология

Формула, которая принимает значение «истина» на всех интерпретациях (наборах значений переменных).

То же, что и тождественно истинная формулаилиобщезначимая формула.

Теорема исчисления высказывания

Формула называется теоремой исчисления высказывания (как аксиоматической теории), если в ней существует вывод, в котором последней формулой является . Этот вывод называется выводом формулы .

Терм

Любой аргумент предиката .

Тождественно истинная формула

Формула, которая принимает значение «истина» на всех интерпретациях (наборах значений переменных).

То же, что и тавтологияилиобщезначимая формула.

Тождественно ложная формула

Формула, которая принимает значение «ложь» на всех интерпретациях.

То же, что и противоречивая формулаилиневыполнимая формула.

Универс

Множество значений , которое может принимать в предикате .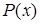

То же, что область определения предикатаилипредметная область.

Условие

В импликации 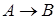высказывание называется условием.

То же, что и антецедент, посылка.