Закон исключенного третьего 3 страница

Каждой конституенте соответствует одна ячейка таблицы. Нуль или единица в ячейке определяет значение функции на данной интерпретации.

При таком расположении минтермы (макстермы), к которым применима операция склеивания, располагаются в соседних ячейках карты, и склеивание производится графически посредством объединения ячеек в группы.

Пример.

Карты Карно для функций двух переменных имеют вид таблицы 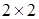(табл. 8.1), где столбцы соответствуют значениям первой переменной, а строки − значениям второй переменной функции 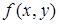(в ячейках указаны соответствующие минтермы в виде формул с абстрактными переменными).

Таблица 8.1 − Структура карты Карно для двух переменных

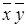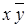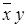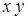Пример.

Структура карты Карно для функции трех переменных 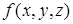имеет вид таблицы 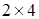(в ячейках указаны соответствующие минтермы в виде формул с абстрактными переменными) (см. табл. 8.2).

Таблица 8.2 − Структура карты Карно для трех переменных

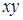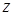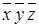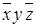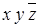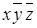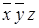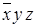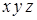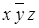Для конкретной булевой функции карта Карно заполняется следующим образом. В ячейки, соответствующие интерпретациям, на которых функция равна единице, записывают единицы. Указанные ячейки соответствуют конституентам единицы, присутствующим в СДНФ функции. В остальные ячейки записывают нули.

Пример.

Построить карту Карно для функции .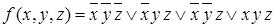

В ячейки таблицы, соответствующие минтермам данной СДНФ, записываем единицы, в остальные ячейки − нули (см. табл. 8.3).

Таблица 8.3 − Карта Карно для функции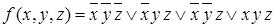

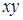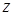К конституентам единицы, соответствующим любым двум соседним ячейкам, можно применить операцию склеивания, так как они отличаются только одной переменной. На карте Карно для функции трех переменных каждая ячейка имеет три соседние ячейки, на карте Карно для функции четырех переменных − четыре, на карте Карно для функции пяти переменных − пять и т.д.

При минимизации на множестве ДНФ в склеивании участвуют только ячейки, содержащие единицы. Как правило, в картах Карно нули в ячейках не указывают, оставляя данные ячейки пустыми.

Пример.

В таблицах 8.4 и 8.5 приведены карты Карно для трех переменных с отмеченными соседними ячейками для ячеек А и В.

Таблица 8.4 − Карта Карно для функции 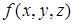с отмеченными соседними ячейками для ячейки А

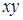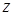			А

Таблица 8.5 − Карта Карно для функции 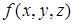с отмеченными соседними ячейками для ячейки В

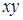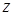				В

Правило склеивания ячеек и записи минимальной ДНФ:

1.Строится карта Карно, соответствующая данной функции.

2. Ячейки объединяются в группы, обозначающие операции склеивания. В объединении участвуют только соседние ячейки, в которых находятся единицы. В группу объединяется только то количество ячеек, которое равно 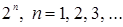. При этом группа может иметь только прямоугольную или квадратную форму.

3. Решается задача склеивания, которая заключается в нахождении набора максимальных групп ячеек. Максимальная группа − это группа, которая не входит целиком ни в одну другую группу и соответствует простой импликанте функции. Количество групп в таком наборе должно быть минимальным, так как такая группа соответствует минимальной тупиковой ДНФ. Каждая единица карты Карно должна входить хотя бы в одну группу, что обеспечивает покрытие функции полученным набором импликант.

4. Каждая группа ячеек, полученная после склеивания, соответствует той импликанте функции, реальные переменные которой имеют одинаковое значение для всех ячеек группы. Переменные берутся без отрицания, если им соответствуют единичные значения, и с отрицанием − в противном случае.

5. Дизъюнкция всех полученных простых импликант представляет собой результат минимизации формулы и является минимальной ДНФ.

Пример.

Найти минимальную ДНФ функции .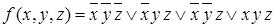

Запишем исходную карту Карно для заданной функции (табл. 8.6).

Таблица 8.6 − Исходная карта Карно для заданной функции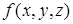

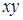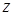Используем графический способ склеивания, объединяя соседние единицы таблицы в группы (нули опускаем). Результатом являются две импликанты А и В (рис. 8.1).

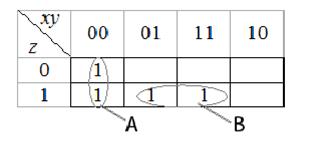
Рисунок 8.1 − Определение импликант функции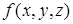

Импликанта .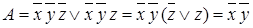

Импликанта .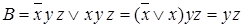

Таким образом, получим минимальную ДНФ в виде .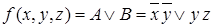

Карта Карно для функции четырех переменных имеет размер 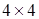. Правила склеивания ячеек и записи результирующей формулы остаются прежними.

Рассмотрим построение карты Карно для функции пяти переменных, которая представляет в пространстве двухслойный параллелепипед, где каждый слой соответствует карте Карно от первых четырех переменных функции. Первый слой представляет собой на плоскости всевозможные интерпретации, при которых пятая переменная равна нулю. Вторым слоем являются всевозможные интерпретации, при которых пятая переменная равна единице. Каждая ячейка на карте Карно для функции пяти переменных имеет пять соседних ячеек: четыре на своем слое карты и пятую − на соседней, т.е. ячейку, которая совпадает с данной, если разместить слои карты один поверх другого. Объединение ячеек в группы на каждом слое карты осуществляется, как и в случае четырех переменных. В данном случае можно склеивать две одинаковые группы, находящиеся на разных слоях карты, расположение которых совпадает, если поместить один слой карты поверх другого.

Пример.Построить минимальную ДНФ для функции

.

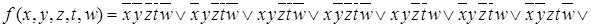
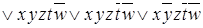Построим карту Карно для данной функции (рис. 8.2).

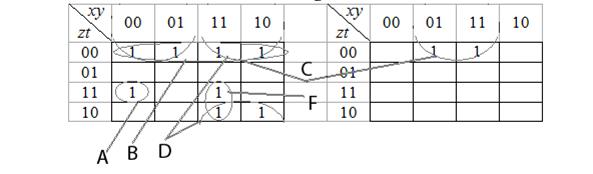
Рисунок 8.2 − Карта Карно для функции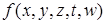

Простые импликанты, входящие в минимальную ДНФ, имеют вид: , , , , .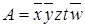

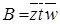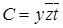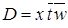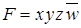Минимальная ДНФ записывается при объединении импликант 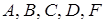знаками дизъюнкции: .

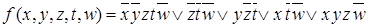Минимизация на множестве КНФ. Для минимизации булевой функции на множестве КНФ используются диаграммы Вейча, построение которых аналогично построению карт Карно. Отличие заключается в том, что на карте помечаются ячейки, соответствующие интерпретациям, на которых функция равна нулю. После этого производится склеивание ячеек, содержащих нули и формирование минимальной КНФ. Для склеивания ячеек используются те же правила, что и при получении минимальной ДНФ. Каждая группа ячеек, полученная в результате склеивания, соответствует дизъюнкции только тех переменных, которые имеют одинаковое значение для всех ячеек группы. Переменные берутся без отрицания, если им соответствует нулевое значение, и с отрицанием − в противном случае. Конъюнкция полученных элементарных дизъюнкций является результатом минимизации формулы.

Пример.

Построить минимальную КНФ функции, заданной картой Карно (диаграммой Вейча), представленной в табл. 8.7.

Таблица 8.7 − Карта Карно (диаграмма Вейча) для функции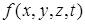

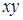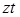Для получения МКНФ необходимо рассмотреть «нулевые» ячейки, максимизируя размеры их групп и минимизируя количество таких групп, и провести операцию склеивания (рис. 8.3).

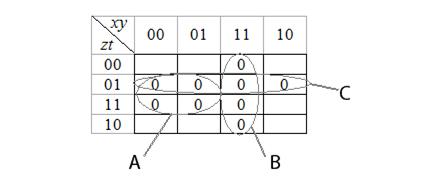
Рисунок 8.3 − Карта Карно (диаграмма Вейча) для булевой функции

Запишем минимальную КНФ, объединив знаками конъюнкции элементарные дизъюнкции: .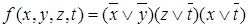

Минимизация частично определенных функций с использованием карт Карно. Для решения некоторых задач могут использоваться не все наборы входных данных, поэтому допустимо любое значение функции на неиспользуемых интерпретациях. Такая функция называется частично определенной. При минимизации такие функции доопределяются так, чтобы получить наиболее экономичную минимальную ДНФ (КНФ).

8.4 Контрольные вопросы и задания

1. Что представляет собой булевый базис? Чем обусловлен выбор базиса при проектировании логических схем?

2. Что представляет собой индекс (коэффициент) простоты? Приведите примеры индексов простоты.

3. Какие существуют подходы для решения задачи минимизации булевых функций в аналитическом виде?

4. Запишите формулы операций дизъюнктивного склеивания и поглощения.

5. Запишите формулы операций конъюнктивного склеивания и поглощения.

6. Дайте определение терминам «импликанта», «имплицента», «простая импликанта», простая «имплицента».

7. Что представляет собой сокращенная ДНФ и сокращенная КНФ?

8. Дайте определение тупиковой ДНФ. Сколько тупиковых ДНФ может иметь булева функция?

9. Какая из ДНФ (КНФ) называется минимальной ДНФ (минимальной КНФ)?

10. Что представляют собой карты Карно (диаграммы Вейча)?

11. Назовите правило склеивания ячеек и записи минимальной ДНФ при использовании карт (диаграмм) Карно.

12. Как осуществляется построение карты Карно для функции пяти переменных?

13. Опишите особенности минимизации булевых функций на множестве КНФ с использованием минимизирующих карт.

14. Каким образом осуществляется минимизация частично определенных функций?

Лекция 9. Алгебра Жегалкина и линейные функции. Функциональная полнота наборов булевых функций

9.1 Алгебра Жегалкина и линейные функции

9.1.1 Основные определения алгебры Жегалкина

Алгебра Жегалкина, названная по имени предложившего её советского ученого, строится на основе операций сложения по модулю 2 и конъюнкции.

Определение.

Алгебра , образованная множеством вместе с операциями конъюнкции ( 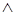), суммы по модулю 2 ( 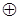) и константами 0 и 1, называется алгеброй Жегалкина.

Пример.

Пусть 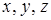- булевы переменные, тогда формула 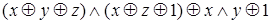, содержащая только операции конъюнкции и суммы по модулю 2, является формулой алгебры Жегалкина.

Непосредственной проверкой по таблицам истинности можно установить следующие основные тождества (свойства этой алгебры):

1) 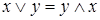, 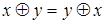- коммутативность;

2) 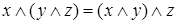, 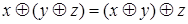- ассоциативность;

3) 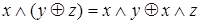- дистрибутивность 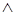относительно ;

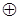4) 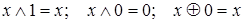- свойства констант.

Все эти свойства подобны обычной алгебре, но в отличие от булевой алгебры закон дистрибутивности суммы по модулю 2 относительно конъюнкции не имеет силы .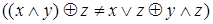

Справедливы также следующие тождества:

5) 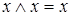- закон идемпотентности для ;

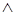6) 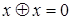- закон приведения подобных при выполнении операции суммы по модулю 2.

Таким образом, в алгебре Жегалкина, как и в булевой алгебре, не могут появляться коэффициенты при переменных и показатели степени.

В алгебре Жегалкина используются следующие соотношения, позволяющие перейти от любой формулы булевой алгебры к соответствующей ей формуле алгебры Жегалкина 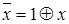, 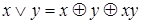и наоборот .

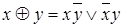Доказательство данных тождеств можно осуществить, используя таблицы истинности функций, либо аналитически, путем тождественных преобразований формул.

Пример.Докажем тождество 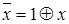, используя таблицы истинности функции (табл. 9.1).

Таблица 9.1 - Таблица истинности функций и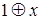

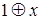Пример.

Докажем формулу 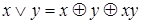аналитически следующим образом:

.

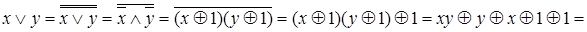
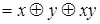Через операции алгебры Жегалкина можно выразить все другие булевы функции:

;

;

;

;

.

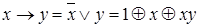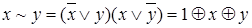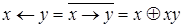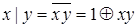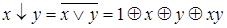9.1.2 Полином Жегалкина

Среди всех эквивалентных представлений функции в алгебре Жегалкина выделяется особый вид формул, называемый полиномом Жегалкина.

Определение.

Полиномом Жегалкина называется конечная сумма по модулю 2 попарно различных элементарных конъюнкций над множеством переменных 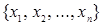. Количество переменных, входящих в элементарную конъюнкцию, называется рангом элементарной конъюнкции. Количество попарно различных элементарных конъюнкций в полиноме называется длиной полинома.

Представление в виде полинома существует и единственно для каждой булевой функции.

Теорема.

Всякая булева функция может быть представлена каноническим полиномом Жегалкина, причем это представление единственное с точностью до перестановки слагаемых и их сомножителей. Для любой булевой функции существует единственный полином Жегалкина.

Для определения полинома Жегалкина можно использовать следующие основные методы:

- метод тождественных преобразований;

- метод неопределенных коэффициентов.

При использовании метода тождественных преобразований для построения полинома Жегалкина функции, заданной некоторой формулой алгебры Жегалкина, необходимо: раскрыть все скобки в данной формуле по закону дистрибутивности и произвести все возможные упрощения с использованием законов действия с константами, идемпотентности и приведения подобных.

Пример.

Представить полиномом Жегалкина логическую функцию импликацию ( ).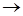

Вначале запишем СДНФ данной функции, затем выразим операции дизъюнкции и отрицания через конъюнкцию и сумму по модулю 2. получив формулу алгебры Жегалкина, пользуясь методом тождественных преобразований, получим полином Жегалкина:

.

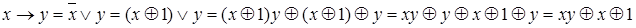9.1.3 Метод неопределенных коэффициентов для нахождения полинома Жегалкина

Метод неопределенных коэффициентов, который можно использовать для нахождения полинома Жегалкина заданной функции, рассмотрим на примере.

Пример.Построить полином Жегалкина для функции импликации с использованием метода неопределенных коэффициентов.

Запишем полином для данной функции в виде суммы по модулю 2 всех возможных элементарных конъюнкций для 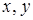с неопределенными коэффициентами 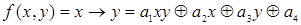, где коэффициенты 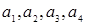принимают значения из множества 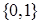и определяют присутствие или отсутствие элементарной конъюнкции в полиноме. Найдем последовательно значения коэффициентов, подставляя значения переменных и функции на различных интерпретациях: 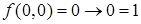, , 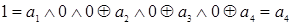следовательно 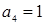. Далее проводим вычисления 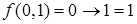, , 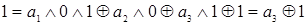следовательно, 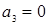. Проводим преобразования на следующей интерпретации 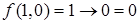, , 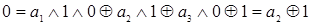откуда следует 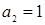. На последней интерпретации: , .

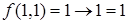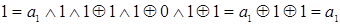Подставив полученные значения коэффициентов 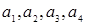, получим полином Жегалкина для функции

.

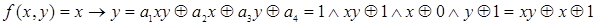Полином Жегалкина, который может быть построен для каждой булевой функции, позволяет определить одно из её важных свойств - линейность.

Определение.

Булева функция называется линейной, если она представляется в алгебре Жегалкина каноническим многочленом (полиномом Жегалкина), не содержащем конъюнкций переменных: 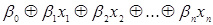, где коэффициенты 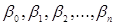, принимающие значение 0 или 1.

Так как всего коэффициентов 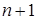, то число различных линейных многочленов будет 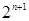. В силу однозначности представления функции полиномом Жегалкина это число выражает и количество линейных функций.

Обозначим через 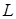класс линейных функций.

Пример.

Отрицание является линейной функцией, т.к. её полином Жегалкина ( 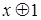) не содержит конъюнкций переменных. Дизъюнкция является нелинейной функцией, поскольку её полином Жегалкина ( 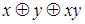) содержит конъюнкцию переменных и . Импликация является нелинейной функцией, так как её полином Жегалкина ( 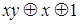) содержит конъюнкцию переменных и . Эквивалентность является линейной функцией, поскольку её полином Жегалкина ( 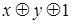)не содержит конъюнкций переменных.

9.2 Функциональная полнота булевых функций

9.2.1 Типы булевых функций

В алгебре логики из множества 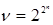различных булевых функций переменных 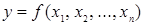выделяются следующие пять типов булевых функций:

а) функции, сохраняющие константу 0;

б) функции, сохраняющие константу 1;

в) самодвойственные функции;

г) монотонные функции;