Семантика пропозициональной динамической логики

Пусть P₀ – множество базисных программ, P – множество всех программ, Р – атомные формулы, F(P) – все формулы, W – множество состояний машины, в которой могут работать программы pÎP. Для каждого p Î P определена модальность [p]. Стало быть, мы должны каждому p поставить в соответствие некоторое отношение доступности R_p Í W ´ W.

Шкала Крипке (или система переходов) будет состоять из пары: (W, (R_p)_pÎP), где W – множество состояний, а R_{p –} отношения R_p Í W ´ W.

Программу можно интерпретировать как множество пар (x, y) Î R_p таких, что после выполнения программы p машина из состояния х перейдёт в состояние y. Каждому атому p Î P ставится в соответствие подмножество h(p) Í W состояний, при которых высказывание р верно.

Интерпретацией называется тройка M = (W, (R_p)_pÎP, h), состоящая из шкалы Крипке и оценки h : P ® P(W), удовлетворяющих соотношениям:

1) R_a È _b = R_a È R_b;

2) R_a ; _b = R_a ° R_b;

3) ;

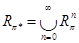4) R_A? = {(x, x) : x Î W и M, x |= A}.

Здесь R_p* – наименьшее рефлексивное транзитивное отношение, содержащее R_p. Расширим h на множество формул F(P), полагая t Î h(A), если и только если M, t |= A. Получим соотношения:

5) h(A Ú B) = h(A) Ú h(B);

6) h(ØA) = W \ h(A);

7) h(<p>A) = {t Î W : (t, u) Î R_p для некоторого u Î h(A)}.

В некоторых случаях под семантикой логики PDL понимают шкалу с расширенной на F(P) оценкой, удовлетворяющие соотношениям 1 – 7.

Аксиомы PDL

Можно ожидать, что для любых формулы А и программы p Î P формула <p*>А, (означающая возможность того, что после кратного применения p машина перейдёт в состояние, удовлетворяющее формуле А), будет равносильна формуле А Ú <p; p*>А, (означающей, что верно А, или А будет, возможно, верно после применения p не менее, чем 1 раз). Получим аксиому:

<p*>А « А Ú <p; p*> А.

Аналогично, исходя из других соображений, получаем аксиомы PDL и формальную теорию:

1) все тавтологии исчисления высказываний;

2) <a>A & <a>B « <a>(A & B);

3) <a>(A Ú B) « <a>A Ú <a>B);

4) <a Ú b>A « <a>A Ú <b>A;

5) <a ; b>A « <a><b>A;

6) <A?>B « A&B;

7) A È <a><a*>A « <a*>A;

8) <a*>A ® A Ú <a*> (ØA & <a>A).

Аксиомы 1 – 3 стандартны для модальных логик. Аксиома 8 равносильна аксиоме Сегерберга:

[a*](A ® [a]A) ® (A ® [a*]A)

и называется аксиомой PDL – индукции.

Правила вывода

; .

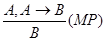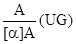Для формальной теории PDL справедливы теорема корректности и полноты.

Логика Хоара

Как мы уже отмечали, логика Хоара предназначалась для дедуктивного доказательства правильности программ. Её формулами являются тройки {А}p{В}, состоящие из предусловия А, программы p и постусловия В. Приведём форму записи, применяемой Хоаром, и её перевод на язык исчисления PDL:

skip	= 1?
fail	= 0?
if A then a else b	= (A? ; a) È (ØA? ; b)
if A1 ® p1 |…| An ® pn fi	= (A1? ; p1) È … È (An? ; pn)
do A ® p od	= (A? ; p)* ; (ØA)?
{A}p{B}	= A ® [p] B

Форма {A}p{B} называется тройкой Хоара. Логика Хоара является формальной теорией для вывода с помощью троек Хоара. Преобразуя аксиомы языка PDL, можно получить следующие правила вывода логики Хоара:

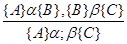(композиция)

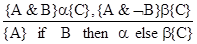(условие)

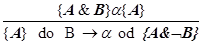(цикл)

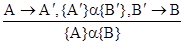(следствие).

Системы Гильберта

Опишем формальную теорию, которая называется системой K:

Аксиомы

1) Если А(Р₁, …, Р_n) – тавтология исчисления высказываний, а В₁, …, В_n – модальные формулы, то А(В₁, …, В_n) – аксиома системы K (пропозициональные тавтологии).

2) Для любых формул А и В формула (А ® В) ® ( А ® В) является аксиомой системы K (аксиома нормальности).

Правила вывода

; .

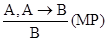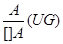Формальная теория, содержащая систему K, называется системой Гильберта.

Строгие системы Гильберта

Добавляя аксиомы к системе K, получаем её усиления. Эти аксиомы соответствуют различным (указанным далее в квадратных скобках) свойствам шкал Крипке (речь о свойствах пойдёт далее):

Т: А ® А [рефлексивность];

D: А ® àА [определённость всюду];

4: А ® А [транзитивность];

В: А ® àА [симметричность];

5: àА ® àА [с аксиомой Т – отношение эквивалентности].

Система К вместе с аксиомой Т обозначается через KТ или S. Такое определение записывается как:

S = K + { А ® А}.

Аналогично, добавляя к K другие аксиомы, получаем следующие системы Гильберта:

K4 = K + { А ® А };

S4 = K + { А ® А, А ® А};

S5 = K + { А ® А, àА ® àА}.

Выводимость. Пусть H – система Гильберта. (Согласно определению, она должна содержать аксиомы и правила вывода системы K).

Определение. Запись 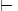_HA означает, что существует последовательность формул А₁, …, А_n таких, что

1) A_n = A;

2) Каждая формула A_i является либо аксиомой системы H, либо получена аз некоторых формул последовательности A₁, …, A_i-1 с помощью правил вывода системы H.

В этом случае А называется теоремой в H, а последовательность A₁, …, A_n – выводом формулы (или доказательством теоремы) А. Число n называется длиной вывода (доказательства).

Пример 1

Последовательность:

A & B ® A, (A & B ® A), (A & B ® A) ® ( (A & B) ® A), (A & B) ® A

является доказательством длины 4 теоремы (A & B) ® A.