Закони й тотожності логіки предикатів
Усі закони й тотожності, які справедливі у логіці висловлювань, залишаються справедливими й у логіці предикатів. Однак у логіці предикатів існують додаткові закони, які використовують для еквівалентного перетворення формул, що містять квантори та змінні.
1. Заміна зв’язаної змінної
Уведення нового позначення зв’язаної змінної не змінює змісту формули логіки предикатів за умови, якщо ніяка вільна змінна у будь-якій частині формули не буде після перейменування зв’язаною змінною , наприклад:
 х Р( х ) =
х Р( х ) =  у Р( у ) ;
у Р( у ) ;
 х Р( х ) =
х Р( х ) =  у Р( у );
у Р( у );
 х
х  у Р( х;у ) =
у Р( х;у ) =  z
z  t ( z, t ).
t ( z, t ).
2. Комутативні властивості кванторів
У логіці предикатів можна змінювати місцями тільки однойменні квантори, наприклад:
 х
х  у Р( х,у ) =
у Р( х,у ) =  у
у  х Р( х,у ) ;
х Р( х,у ) ;
 х
х  у Р( х,у ) =
у Р( х,у ) =  у
у  х Р( х,у ) ;
х Р( х,у ) ;
 х
х  у Р( х,у )
у Р( х,у ) 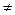
 у
у  х Р( х,у ).
х Р( х,у ).
Приклад 3.5.1. Для предиката  x
x  y ДОРІВНЮЄ(х+1, у ) показати, що зміна місцями кванторів приводить до невідповідності між висловлюваннями до і після зміни місцями кванторів.
y ДОРІВНЮЄ(х+1, у ) показати, що зміна місцями кванторів приводить до невідповідності між висловлюваннями до і після зміни місцями кванторів.
Розв’язання. Заданий предикат є висловлюванням і означає, що для будь-якого числа х існує число у, яке більше його на одиницю. Наведене висловлювання є істинним. Але якщо поміняти порядок розташування кванторів на протилежний, то отримаємо таке висловлювання:  y
y  x ДОРІВНЮЄ( х+1, у ). Одержане висловлювання означає, що існує таке число у (одне), яке на одиницю більше будь-якого числа х. Це висловлювання не відповідає попередньому і є хибним, що підтверджує закон комутативної властивості кванторів.
x ДОРІВНЮЄ( х+1, у ). Одержане висловлювання означає, що існує таке число у (одне), яке на одиницю більше будь-якого числа х. Це висловлювання не відповідає попередньому і є хибним, що підтверджує закон комутативної властивості кванторів.
3. Дистрибутивні властивості кванторів
Нехай формула Р ( х ) містить пов’язану змінну х, а формула Q не містить пов’язаної змінної х й обидві вони задовольняють п.3 означення 3.3.1, тоді

 х ( Р ( х )
х ( Р ( х )  Q ) =
Q ) = 
 х Р ( х )
х Р ( х )  Q;
Q;
 х ( Р ( х )
х ( Р ( х )  Q ) =
Q ) =  х Р ( х )
х Р ( х )  Q;
Q;

 х ( Р ( х )
х ( Р ( х ) 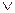 Q ) =
Q ) = 
 х Р ( х )
х Р ( х ) 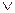 Q;
Q;
 х ( Р ( х )
х ( Р ( х ) 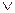 Q ) =
Q ) =  х Р ( х )
х Р ( х ) 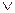 Q .
Q .
Доведемо першу із цих рівностей (інші доводять аналогічно). Нехай х 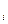
 ,х
,х 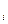
 ...,х
...,х 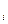
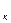 ‒ усі вільні змінні формули
‒ усі вільні змінні формули  х ( Р ( х )
х ( Р ( х )  Q ). Тоді вони будуть усіма вільними змінними формули
Q ). Тоді вони будуть усіма вільними змінними формули 
 х Р ( х )
х Р ( х )  Q.
Q.
Розглянемо довільну інтерпретацію на множині М. Нехай ( a  , a
, a  ,..., а
,..., а 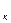 ) ‒ довільний набір значень вільних змінних х
) ‒ довільний набір значень вільних змінних х 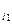 ,х
,х 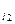 ...,х
...,х 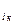 , де а
, де а 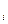
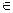 М . Оскільки формула Q не містить пов’язаної змінної х , то можна визначити значення цієї формули на наборі ( a
М . Оскільки формула Q не містить пов’язаної змінної х , то можна визначити значення цієї формули на наборі ( a  , a
, a  ,..., а
,..., а 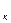 ) у частині , що стосується вільних змінних формули Q. Якщо формула Q на наборі ( a , a
) у частині , що стосується вільних змінних формули Q. Якщо формула Q на наборі ( a , a  ,..., а
,..., а 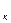 ) набула значення Х , то (
) набула значення Х , то (  х Р( х )
х Р( х )  Q ) на цьому наборі теж Х і для будь-якого елемента а
Q ) на цьому наборі теж Х і для будь-якого елемента а 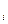
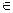 М на наборі ( a
М на наборі ( a  , a
, a  ,..., а
,..., а 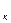 ) своїх вільних змінних х
) своїх вільних змінних х 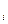
 ,х
,х 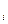
 ...,х
...,х 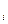
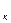 формула Р( х )
формула Р( х )  Q набуває значення Х. Звідси випливає, що
Q набуває значення Х. Звідси випливає, що 
 х Р ( х )
х Р ( х )  Q на цьому наборі теж дорівнює Х. Якщо формула Q на наборі ( a
Q на цьому наборі теж дорівнює Х. Якщо формула Q на наборі ( a  , a
, a  ,..., а
,..., а 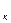 ) набула значення І, то для будь-якого елемента а
) набула значення І, то для будь-якого елемента а 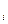
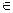 М на наборі ( a
М на наборі ( a  , a
, a  ,..., а
,..., а 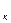 ) формула Р( х )
) формула Р( х )  Q й Р( х ) набувають однакових значень істинності. Звідси випливає, що
Q й Р( х ) набувають однакових значень істинності. Звідси випливає, що  х ( Р( х )
х ( Р( х )  Q ) на наборі ( a
Q ) на наборі ( a  , a
, a  ,..., а
,..., а 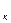 ) тотожна
) тотожна
 х Р( х )
х Р( х )  Q .
Q .
Якщо не вимагати, щоб формула Q не містила пов’язаної змінної х, то справджуватимуться тільки дві рівносильності :
 х ( Р ( х )
х ( Р ( х )  Q ( х )) =
Q ( х )) =  х Р ( х )
х Р ( х ) 
 х Q х ;
х Q х ;
 х ( Р ( х )
х ( Р ( х ) 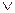 Q ( х )) =
Q ( х )) =  х Р ( х )
х Р ( х ) 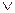
 х Q ( х ) .
х Q ( х ) .
Сформульований дистрибутивний закон справедливий тільки для квантора загальності  при кон’юнкції і квантора існування
при кон’юнкції і квантора існування  при диз’юнкції, оскільки інші комбінації приводять до нерівностей
при диз’юнкції, оскільки інші комбінації приводять до нерівностей
 х ( Р( х )
х ( Р( х ) 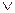 Q( х ))
Q( х )) 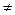
 х Р( х )
х Р( х ) 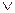
 х Q( х );
х Q( х );
 х ( Р( х )
х ( Р( х )  Q( х ))
Q( х )) 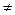
 х Р( х )
х Р( х ) 
 х Q х ).
х Q х ).
Для подолання цього обмеження дистрибутивного закону потрібно використовувати заміну зв’язаної змінної:
 х Р( х )
х Р( х ) 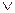 Q( х ) =
Q( х ) =  х Р( х )
х Р( х ) 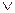
 у Q( у )=
у Q( у )=
=  х
х  у ( Р( х )
у ( Р( х ) 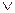 Q( у ) ;
Q( у ) ;
 х Р( х )
х Р( х ) 
 х Q( х ) =
х Q( х ) =  х Р( х )
х Р( х ) 
 у Q( у )=
у Q( у )=
=  х
х  у ( Р( х )
у ( Р( х )  Q( у )).
Q( у )).
4. Закон де Моргана для кванторів
Нехай Р (х) – формула, що містить пов’язані й вільні змінні. Тоді справджуються рівносильності 
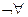 хР ( х ) =
хР ( х ) =  х
х 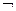 Р( х ); (3.5.1)
Р( х ); (3.5.1) 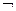
 х Р( х ) =
х Р( х ) =  х
х 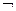 Р( х ). (3.5.2)
Р( х ). (3.5.2) 
Доведемо спочатку рівносильність 3.5.1. Нехай х 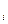
 ,х
,х 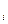
 ...,х
...,х 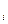
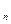 ‒ множина всіх вільних змінних формули Р , відмінних від пов’язаних змінних х. Покажемо, що на будь-якому наборі значень вільних змінних (a
‒ множина всіх вільних змінних формули Р , відмінних від пов’язаних змінних х. Покажемо, що на будь-якому наборі значень вільних змінних (a  , a
, a  ,..., а
,..., а 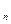 ), а
), а 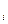
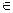 М, формули
М, формули 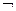
 х Р( х ) і
х Р( х ) і  х
х 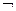 Р( х ) набувають однакових значень істинності. При цьому можливі два випадки.
Р( х ) набувають однакових значень істинності. При цьому можливі два випадки.
1. Для будь-якого елемента а 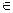 М Р( х )= І на наборі ( а , a
М Р( х )= І на наборі ( а , a  , a
, a  ,..., а
,..., а 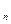 ).
).
2. Для деякого елемента а 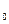
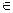 М Р ( х ) = Х на наборі ( а
М Р ( х ) = Х на наборі ( а 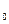 , a
, a  , a
, a  ,..., а
,..., а 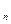 ).
).
У першому випадку для будь-якого елемента а 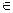 М маємо
М маємо 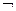 Р( х ) =Х на наборі ( a
Р( х ) =Х на наборі ( a  , a
, a  ,..., а
,..., а 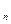 ). Звідси за означенням
). Звідси за означенням  х
х 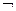 Р( х ) = Х на наборі ( a
Р( х ) = Х на наборі ( a  , a
, a  ,..., а
,..., а 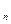 ), з іншого боку,
), з іншого боку,  х Р( х ) = І, а
х Р( х ) = І, а 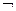
 х Р ( х ) = Х на наборі
х Р ( х ) = Х на наборі
( a  , , a
, , a  ,..., а
,..., а 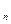 ) .
) .
У другому випадку для елемента а 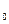
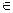 М маємо
М маємо
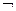 Р(х) = І на наборі (а
Р(х) = І на наборі (а 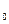 , a
, a  , a
, a  ,..., а
,..., а 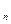 ). Звідси
). Звідси  х
х 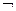 Р( х ) = І на наборі ( a
Р( х ) = І на наборі ( a  , a
, a  ,..., а
,..., а 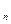 ). З іншого боку,
). З іншого боку,  х Р(х) = Х , а
х Р(х) = Х , а 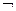
 х Р ( х ) = І на наборі ( a
х Р ( х ) = І на наборі ( a  , a
, a  ,..., а
,..., а  ), що й потрібно було довести для рівносильності формули 3.5.1. Доведення рівносильності формули 3.5.2 аналогічне описаному для формули 3.5.1.
), що й потрібно було довести для рівносильності формули 3.5.1. Доведення рівносильності формули 3.5.2 аналогічне описаному для формули 3.5.1.
