Программирование с отходом назад
Основой программ искусственного интеллекта, независимо от то-го, к чему он прилагается – программированию игр, выбору решений, распознаванию образов и т.п., – является программирование перебора вариантов. Программирование перебора вариантов - это сложная задача, так как алгоритмы перебора ищут решения не по заданным правилам вычислений, а путем проб и ошибок, и схема не укладывается в схемы циклов, имеющихся в языках программирования. Ситуация зачастую осложняется тем, что прямыми методами перебор всех возможных вариантов невозможно осуществить из-за их огромного количества.
Метод программирования с отходом назад позволяет осуществить организованный исчерпывающий поиск требуемого решения задачи. При этом часто удается избежать перебора всех возможных вариантов.
Пример. Рассмотрим пример, который демонстрирует основные свойства, общие для всех алгоритмов с отходом назад. Задача о восьми ферзях. Найти все способы расстановки на шахматной доске 8 ферзей так, чтобы они не угрожали друг другу, т.е. чтобы на доске 8x8 никакие два ферзя не стояли на одной вертикали, горизонтали или диагонали.
Очевидно, что больше 8 ферзей на доске 8x8 расставить нельзя, так как все ферзи должны стоять на разных горизонталях (или вертикалях), а их всего 8. Однако значительно труднее подсчитать общее число таких расстановок, в чем собственно и состоит задача.
Множество всех возможных расстановок ферзей, среди которых надо отыскать требуемые, удобно представить с помощью ориентированного дерева и по нему осуществлять поиск нужного варианта (рис. 2). Ориентированное дерево - это связный граф без циклов с выделенной вершиной (корнем), в котором между корнем и любой другой вершиной существует единственный путь. У дерева будет 9 уровней, номер уровня I определяет номер вертикали, на которую устанавливается 1-й ферзь. Восемь ветвей, выходящих из каждой вершины 1-го уровня, соответствует восьми возможным горизонтальным позициям ферзя, устанавливаемого на (i+1)-й вертикали.
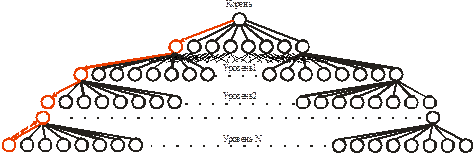
Рисунок 2
По условию задачи ферзи не должны бить друг друга. Поэтому из рассмотрения исключаем вершины дерева, которые соответствуют уже занятым горизонталям и диагоналям. Тогда алгоритм перебора возможных вариантов сводится к прохождению всех связанных вершин дерева: двигаемся вниз по дереву (начиная, например, с левой ветви) до тех пор, пока не достигнем вершины последнего уровня. Если попытка установить (i+1)-го ферзя оказывается неудачной, то отходим назад на один уровень и проверяем, можем ли спуститься опять по другой ветви. Если такой спуск возможен, то опять по самой левой из непройденных ветвей спускаемся вниз (отход в бок), иначе отходим назад еще на один уровень и пытаемся спуститься по следующей из пройденных ветвей и т.д., пока не переберем все 8 горизонтальных полей для (i+1)-й вертикали. Если успешно достигнута вершина последнего уровня, то значит найден очередной требуемый вариант расстановки ферзей. Тогда возвращаемся к корню и начинаем движение вниз по следующей из непройденных ветвей и т.д. до тех пор, пока не останется не-пройденных ветвей. При такой организации перебора вариантов возможно не больше 88 =224 вариантов, что приблизительно равно 106 вариантов. На самом деле их будет гораздо меньше, так как должно выполняться условие, что ферзи не бьют друг друга.
