Непосредственные умозаключения по логическому квадрату, умозаключения обращения, превращения и противопоставления.

Обращение – одна из них. Логический смысл данной операции заключается в том, что субъект (S) и предикат (Р) суждения меняются местами, не меняя качества суждения. Количество может как сохраняться (при чистом обращении), так и меняться (обращение с ограничением).
Общая структура этой операции такова:

S есть (не-есть) Р

Р есть (не-есть) S

Читается: «если S есть (не-есть) Р, то Р есть (не-есть) S».

С учетом распределенности терминов, суждения типа А, Е, I, О обращаются следующим образом:

I. А → I.

Суждение А обращается в суждение I: «Если все S есть Р, то некоторые Р есть S». Это обращение с ограничением. Ограничение связано с тем, что понятия S и Р взяты в разном объеме. В этом легко убедиться при помощи схемы:

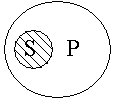Например: «Если все калькуляторы (S) являются вычислительными устройствами (Р), то лишь некоторые вычислительные устройства (Р) являются калькуляторами (S)».

II. Е → Е.

Суждение Е обращается в суждение Е без ограничения: «Если ни одно S не-есть Р, то ни одно Р не есть S». Схематически это выглядит так:

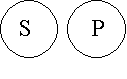
Подумайте... Проиллюстрируйте это на собственных примерах.

III. I → I.

Суждение I обращается в I также без ограничения, т.е. с сохранением качества и количества суждения: «если некоторые S есть Р, то некоторые Р есть S» Схематически это доказывается так:

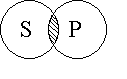Например: «Если некоторые, знающие языки программирования (S), являются студентами БГУИР (P), то некоторые студенты БГУИР (P) знают языки программирования (S)».

IV. О → .

Суждение О не обращается.

Превращение Превращение – логическая операция с простыми суждениями, в ходе которой меняется качество суждения (утвердительная связка заменяется на отрицательную и наоборот), субъект и предикат остаются на своих местах (не обращаются), а предикат исходного суждения заменяется на противоречивый в превращенном суждении.

Общая структура операции превращения:

S есть (не-есть) Р

S не-есть (есть) не-P

«Если S есть (не-есть) Р, то S не-есть (есть) не-P».

В результате превращения простых категорических суждений получается:

Вид исходного суждения	Вид превращенного суждения
А «Все S есть Р»	Е «Все S не-есть не-Р»
Е «Все S не-есть Р»	А «Все S есть не-Р»
I «Некоторые S есть Р»	О «Некоторые S не-есть не-Р»
О «Некоторые S не-есть Р»	I «Некоторые S есть не-Р»

Противопоставление Противопоставление – логическая операция с простыми суждениями, включающая и обращение, и превращение суждений. Делать это можно в разной последовательности. Либо вначале исходное суждение обращается («Все S есть Р» → «Некоторые Р есть S»), а затем обращенное суждение превращается («Некоторые Р есть S» → «Некоторые Р не-есть не-S»). Либо вначале исходное суждение превращается («Все S есть Р» → «Все S не-есть не-Р»), а затем превращенное суждение обращается («Все S не-есть не-Р» → «Все не-Р не-есть S»).

В первом случае в результате получается противопоставление субъекту (S). Во втором – противопоставление предикату (P).

Упражнения:

1.Укажите вид следующих умозаключений:
1.1. Все планеты Солнечной системы - небесные тела
Некоторые небесные тела входят в Солнечную систему - тродукт, достоверное.
1.2. Ни один вулкан не является безопасным
Следовательно, все вулканы являются. небезопасными - тродукт, достоверное.
1.3. Все христиане не являются язычниками .
Следовательно, некоторые не язычники – христиане - тродукт, достоверное.
2. Проверьте правильность следующих непосредственных умозаключений по логическому квадрату:
2.1.Если верно, что все квадраты являются равносторонними прямоугольниками, то неверно, что некоторые квадраты не являются равносторонними прямоугольниками. - Ложно
2.2. Если неверно, что ни одно преступление не раскрывается, то также неверно и то, что все преступления раскрываются.- Ложно
2.3. Если неверно, что все импрессионисты - французы, то следует признать, что некоторые из них не были французами.- Истинно
2.4. Если верно, что некоторые писатели являются лауреатами Нобелевской премии, то также верно и то, что некоторые из писателей ими не являются. - Истинно

ТЕМА № 17

"Простой категорический силлогизм".

План:

1. Определение силлогизма как дедуктивного опосредованного вывода.
2. Структура и общие правила силлогизма.
3. Аксиома силлогизма.

Определение силлогизма как дедуктивного опосредованного вывода.
Простой категорический силлогизм (от греч. sillogismos- выведение, сосчитывание) - это дедуктивное опосредованное умозаключение, состоящее из двух суждений, имеющих субъектно–предикатную форму и заключения, также имеющего субъектно–предикатную форму. Напомним, что субьектно-предикатная форма свойственна всем простым категорическим суждениям. Поэтому простой категорический силлогизм можно определить как «состоящий из двух простых категорических суждений и заключения».

Структура и общие правила силлогизма.
Силлогизм состоит из трех терминов. В отличие от терминов суждения(S-субъекта и P-предиката), они называются терминами силлогизма. Их так же, как и посылок, три. Под терминами понимают уже не суждения, а понятия, входящие в умозаключение.

1. Больший термин силлогизма – понятие, совпадающее с предикатом заключения. Обозначается буквой P. Посылка, в которую он входит, называется большей.

2. Меньший термин силлогизма – это понятие, совпадающее с субъектом заключения. Обозначается буквой S. Посылка, в которую он входит, называется меньшей. Больший и меньший термины образуют группу крайних терминов силлогизма. Каждый из них входит только в одну из посылок.

3. Средний термин силлогизма – это понятие, которое присутствует в каждой из посылок и отсутствует в заключении. Обозначается буквой М. Данный термин играет роль «посредника» в умозаключении. Он называется «средним», так как связывает по смыслу крайние термины в посылках. А вывод об отношении крайних терминов в заключении делается на основании отношения крайних терминов к среднему в посылках. Иначе говоря, смысл простого категоричесского силлогизма сводится к тому, чтобы установить: «S есть P» или «S не-есть P»? Но делается это своеобразно, опосредованно, через «посредника»-М, в три этапа:

а) в большей посылке устанавливается отношение предиката и среднего термина, т.е. она может быть только двух видов: M-P; P-M;
б) в меньшей посылке устанавливается отношение субъекта к среднему термину. Значит, и здесь может быть только два варианта отношений: S - M; M – S.
в) выяснив поочередно «отношения» со средним термином, крайние термины могут теперь выяснить отношение «между собой»: (S есть P или S не-есть P), что и образует логический смысл заключения простого категорического силлогизма. Логическая роль среднего термина «играется» в посылках; в заключении же он уже не нужен. Поэтому средний термин никогда не выходит в заключение. А если это происходит, то это означает логическую ошибку и неправильно построенный вывод. В целом это может выглядеть следующим образом:

M-P Все государства (М) имеют столицу (Р)

S-M Конго (S) – государство (M)

S-P Конго (S) имеет столицу (P)

Как "узнать" средний термин? Легко заметить, что средний термин «звучит» дважды в посылках и «не звучит» в заключении. В нашем примере:

Средний термин (М) - понятие «государство», Больший термин (Р) - столица, Меньший термин(S)-Конго.

Самое развернутое определение простого категорического силлогизма будет следующим: простой категорический силлогизм – это умозаключение об отношении двух крайних терминов на основании их отношения к среднему термину. Значение силлогизма в мыслительной практике очень велико. Оно опирается на общие знания («Все государства имеют столицу») и позволяет установить, подходит ли интересующий случай под общее правило? («Имеет ли Конго столицу, если оно - государство?»). В итоге получается утвердительный или отрицательный ответ.

Аксиома силлогизма.

Логическим обоснованием правильности вывода типа ПКС является аксиома силлогизма. Аксиома – это такое исходное положение, которое считается истинным без доказательств. Аксиома силлогизма – это то положение, которое кладется в основу данной формы вывода и устанавливает два отношения между понятиями силлогизма:

1. по содержанию - между понятиями, входящими в посылки, и понятиями, входящими в заключение. В содержательном плане аксиома силлогизма устанавливает отношение между предметами и их признаками. Ее суть: признак признака некоторой вещи есть признак самой этой вещи; то, что противоречит признаку некоторой вещи, противоречит и самой вещи. Кратко она звучит: «признак признака есть признак вещи». Поясним это на примере:

Все металлы (М) - электропроводны (Р)

Серебро (S) – металл (M)

Серебро (S) электропроводно (P)

1. Нам необходимо установить отношение между предметом («серебро»-S) и его возможными признаками. В ходе рассуждения выясняется, что серебро обладает признаком «быть металлом» (М). Но у этого признака есть свой признак – «быть электропроводным» (Р). Значит, серебро «приобретает» заодно и этот вторичный признак или признак признака, что и составляет заключение: «Серебро - электропроводно» или S есть P;

3. по объему - между понятиями, входящими в силлогизм. Все, что утверждается или отрицается относительно всех предметов класса, утверждается или отрицается как относительно каждого предмета, так и любой части предметов этого класса. Раньше уже говорилось, что отношения между понятиями по обьему в логике принято иллюстрировать через круги Эйлера.

Воспользуемся этим приемом.
В случае, если силлогизм состоит из утвердительных суждений, аксиома схематически выглядит так (смотри предыдущий пример):

В случае, если в силлогизме имеется отрицательная посылка, отношение между терминами силлогизма, согласно аксиоме, выглядит следующим образом:

Пример:

Дерево (М) не проводит ток(Р)

Береза (S) - дерево (М)

Береза(S) не проводит ток (Р)

Истинность простого категорического силлогизма зависит не только от истинности исходных суждений, но и (как было сказано ранее) от правильного сочетания истинных посылок. Для этого необходимо соблюдать ряд правил.

Упражнения:

1. Укажите структуру и проверьте соблюдение общих правил силлогизма в следующих умозаключениях:

1.1. Каждый, совершивший преступление, должен быть подвергнут наказанию; Х также должен быть подвергнут наказанию, т.к. он совершил преступление. 1)MPSPSM
1.2. Сахар - углевод, значит, он, как и все углеводы, горюч. 2) SMSMP
1.3.Ни один древний грек не знал латыни. Аристотель – древний грек. Аристотель не знал латыни. 3) MPSMSP
1.4.Все химические элементы обладают атомным весом. Гелий -химический элемент. Гелий обладает атомным весом. 4) MPSMSP
1.5. Все фрукты являются полезными для здоровья, и все морепродукты -тоже. Значит, все морепродукты - фрукты. 5) SPSPSS – нарушено правило «всех терминов»

ТЕМА №18

"Фигуры и модусы простого категорического силлогизма".

План:

1. Фигуры и правила фигур простого категорического силлогизма.
2. Образование модусов простого силлогизма и проверка их правильности.