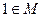Минимизация сложных высказываний методом Квайна

Алгоритм:

1. Получить СДНФ.

2. Получить сокращенную ДНФ (СкДНФ), используя следующие равносильности:

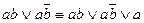- неполное склеивание;

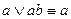- поглощение.

3. Построить импликантную матрицу, с помощью которой получить МДНФ.

Пример.

1. 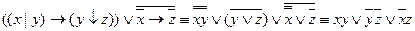- ДНФ

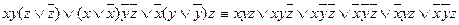- СДНФ

1 2 3 4 5 6

2. Применяя операции склеивания, получаем СкДНФ.

1-2: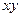
1-5: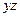
2-3: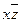
3-4: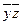
4-6: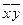
5-6: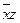

3. Импликантная матрица

	+	+
	+				+
		+	+
			+	+
				+		+
					+	+

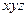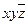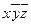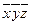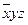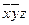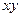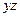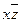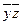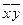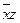Выбираем импликанты, которые поглощают все конституенты единицы.

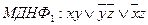
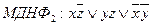
Полные системы функций

1.9.1. Система функций { }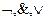

Теорема. Всякая булева функция порождается некоторой формулой, в которой есть только операции .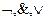

Доказательство. Пусть 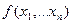некоторая булева функция. Для нее можно поострить таблицу истинности, в которой будет 2ⁿ строк. Каждую строку можно представить в виде конъюнкции переменных х₁,…х_n, куда входит либо 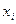, либо 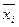. Если значение конъюнкции будет равно 1, то всю функцию можно представить в виде дизъюнкции этих конъюнкций.

Пример.

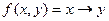
x	y	f(x,y)

Получим СДНФ, используя таблицу истинности.

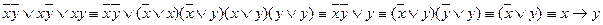Возникает вопрос: Существуют ли другие системы булевых функций, с помощью которых можно выразить все другие функции?

Замкнутые классы

Пусть 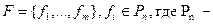множество булевых функций от n переменных.

Замыканием F ([F]) называется множество всех булевых функций, реализуемых формулами над F.

Множество функций (класс) называется замкнутым, если [F]=F.

Рассмотрим следующие классы функций.

1. Класс функций, сохраняющих 0:

.

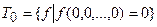2. Класс функций, сохраняющих 1:

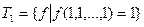
3. Класс самодвойственных функций:

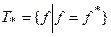, где .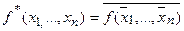

4. Класс монотонных функций

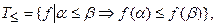где .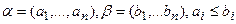

5. Класс линейных функций

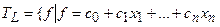, где + - означает сложение по модулю 2, а знак конъюнкции опущен.

Теорема. Классы Т₀, Т₁, Т_*, Т_М, T_L – замкнуты.

Доказательство. Чтобы доказать, что некоторый класс F замкнут достаточно показать, что, если формула реализована в виде формулы над F, то она принадлежит F.

Рассмотрим доказательство для одного класса функций Т₀.

Пусть 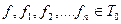и 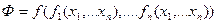. Тогда .

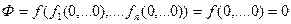Аналогичные доказательства можно привести для остальных классов.

Функциональная полнота

Класс функций F называется полным, если его замыкание совпадает с P_n:

.

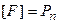Другими словами, множество функций F образует полную систему, если любая функция реализуема в виде формулы над F.

Теорема.

Пусть заданы две системы функци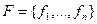й и .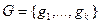

Тогда, если система F – полная и все функции из F реализуемы формулами над G, то система G тоже полная.

Доказательство. Пусть h – произвольная функция, 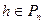. Тогда [F]=P_n, следовательно, h реализуема формулой 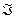, базисом которой является F ( 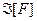). Если выполнить замену подформулы fi на подформулу 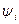в формуле 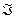, то мы получим формулу над G.

Следовательно, функция h реализуется формулой .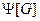

Примеры:

1. Система { 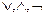} – полная, т. к. любая логическая операция может быть выражена через дизъюнкцию, конъюнкцию и отрицание;

2. Система { 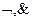} – полная, т. к.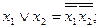

3. Система { 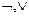} – полная, т. к.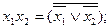

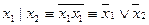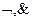4. Система {|} – полная, т. к. , а { }и{ 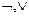} – полные системы.

5. Система { 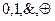} – полная, т. к. 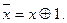Представление логической операции системой{ 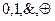}называется полиномом Жегалкина. Таким образом, всякая логическая операция представима в ви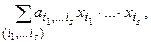де

где 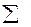- сложение по модулю 2, знак · обозначает конъюнкцию, .

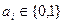Теорема Поста: Система логических операций полна тогда и только тогда, когда она содержит хотя бы одну функцию, не сохраняющую 0, одну функцию, не сохраняющую 1, хотя бы одну несамодвойственную функцию, хотя бы одну нелинейную функцию и хотя бы одну немонотонную функцию.

Пример.

Докажем полноту системы {Å,Ú,1}.

f	T0	T1	T*	TL	TM	В каждом столбце должен быть хотя бы один «-»
xÅy	+	-	-	+	-
xÚy	+	+	-	-	+
	-	+	-	+	+

1.

Проверка на принадлежность классу T₀.

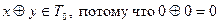
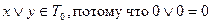
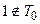
2.

Проверка на принадлежность классу T₁.

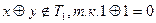
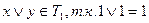
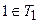
3.

Проверка на принадлежность классу T*.

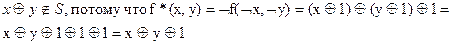
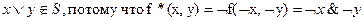
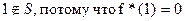
4.

Проверка на принадлежность классу T_L.

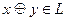
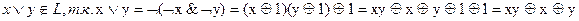
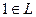
5.

Проверка на принадлежность классу T_M.

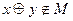
f(0,0)=0

f(0,1)=1

f(1,0)=1

f(1,1)=0

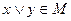
f(0,0)=0

f(0,1)=1

f(1,0)=1

f(1,1)=1