Простой категорический силлогизм. Части, общие правила.

Категорический силлогизм— это вид дедуктивного умозак­лючения, в котором из двух истинных категорических суждений, где S и Р связаны средним термином, при соблюдении правил необходимо следует заключение.

Силлогизм происходит от греческого syllogismos (сосчитывание, выведение следствия).

В составе категорического силлогизма имеются две посылки и заключение.

Все металлы (М) электропроводны (Р) — большая посылка.

Медь (S) есть металл (М) — меньшая посылка.

Медь (S) электропроводна (Р) — заключение.

Понятия, входящие в состав силлогизма, называются тер­минами силлогизма. В приведенном примере терминами являют­ся: Р («электропроводник») — больший термин, это предикат заключения; S («медь») — меньший термин, это субъект заклю­чения; М («металл») — средний термин, служащий в посылках для связывания S и Р и отсутствующий в заключении (рис. 43).

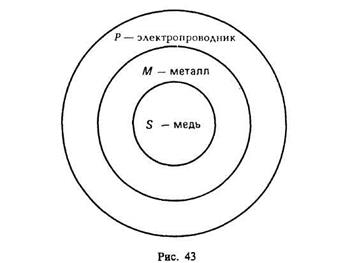
Посылка, содержащая предикат заключения (т. е. больший термин), называется большей посылкой. Посылка, содержащая субъект заключения (т. е. меньший термин), называется меньшей посылкой.

В основе вывода по категорическому силлогизму лежит акси­ома силлогизма. «Все, что утверждается (отрицается) о роде (или классе), необходимо утверждается (отрицается) о виде (или о чле­не данного класса), принадлежащем к данному роду». Иными словами: то, что мы утверждаем о металле как роде, мы утверж­даем и о его виде — меди, а именно утверждаем его признак «быть электропроводником».

Фигуры категорического силлогизма

Фигурами категорического силлогизма называются формы силлогизма, различаемые по положению среднего термина М в посылках. Различаются четыре фигуры (рис. 44).

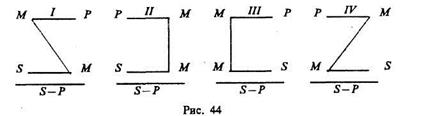
Примеры:

1. Все злаки (М) — растения (Р). 2. Все ужи (Р) — пресмыкающиеся (М).

Рожь (S) — злак (М). Это животное (S) не является пре-

_____________________________ смыкающимся (М).

Рожь (S) — растение (Р). -------------------------------------------

3. Все углероды (М) — простые Это животное (S) не является ужом(Р).

тела (Р).

Все углероды (М) — электро- 4. Все киты (Р) — млекопитающие (М).

проводны (S). Ни одно млекопитающее (М) не есть рыба (5).

__________________________ ------------------------------------------------

Некоторые электропроводники Ни одна рыба (S) не есть кит (Р).

(S) — простые тела (Р).

Особые правила фигур

I фигура. Большая посылка должна быть общей, меньшая — утвердительной.

II фигура. Большая посылка общая и одна из посылок, а также заключение отрицательные.

III фигура. Меньшая посылка должна быть утвердительной, а заключение — частное.

IV фигура. Общеутвердительных заключений не дает.

20.Особенности 1-ой и 3-ей фигур силлогизма. Возможные модусы.

Модусами фигур категорического силлогизма называются разновидности силлогизма, отличающиеся друг от друга качест­венной и количественной характеристикой входящих в них посы­лок и заключения.

I фигура

В 1-й фигуре средний термин занимает место субъекта в большей посылке предиката в меньшей.

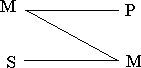
Пример:

Все металлы (М) - электропроводны (Р)

Медь (S) - металл (М)

Медь (S) - электропроводна (Р)

Правила 1-й фигуры:

1) бoльшая посылка должна быть общей (А или Е);

2) мeньшая посылка должна быть утвердительной (А или I).

Все студенты - люди

Ни один профессор не является студентом

Ни один профессор не является человеком - неправильный силлогизм, т. к. меньшая посылка отрицательная

Некоторые люди заслуживают уважения

Все преступники - люди

Некоторые преступники заслуживают уважения - неправильный силлогизм, т. к. бoльшая посылка является частным суждением

I фигура имеет следующие правильные модусы (буквы обо­значают последовательно количество и качество большей посыл­ки, меньшей и заключения): ААА, ЕАЕ, All, ЕЮ. Пример 1 ил­люстрирует модус ААА.

III фигура

В 3-ей фигуре средний термин занимает место субъекта в обеих посылках.

Пример:

Ни один страус (М) не летает (Р)

Все страусы (М) птицы (S)

Некоторые птицы (S) не летают (P)

Правила 3-й фигуры:

1) мeньшая посылка должна быть утвердительным суждением (А, I);

2) заключение должно быть частным суждением (I, О).

Пример:

Все студенты являются людьми

Некоторые студенты не являются мужчинами

Некоторые мужчины не являются людьми - неверно, т. к. меньшая посылка отрицательная

Все студенты являются людьми

Все студенты являются живыми существами

Все живые существа являются студентами - неверно, т. к. заключением является общее суждение.

III фигура имеет правильные модусы: AAI, EAO, IAI, ОАО, АП, ЕЮ. Модус AAI представлен примером 3.