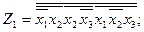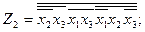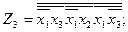Синтез комбинационных схем с несколькими выходами

В предыдущей главе рассматривались примеры синтеза комбинационных схем с одним выходом на контактных и бесконтактных элементах. Однако в общем случае комбинационные схемы могут иметь m входов и п выходов, т.е. могут реализовать n функций вида

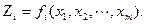
При количестве входов равном m комбинационная схема (автомат) может находиться в 2^m состояниях, причем значения выходов могут определяться не для всех возможных состоянии схемы. Тогда задание автомата может быть представлено в виде функций:

,

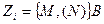или

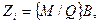
где М - подмножество состояний схемы, при которых функция Z_i, принимает значение 1 (обязательное подмножество);

N - условное подмножество или подмножество состояний схемы, при которых значение выходной функции Z (безразлично);

Q - подмножество состояний схемы, при которых Z_i = 0 (запрещенное подмножество);

В - база или набор аргументов ФАЛ.

Пример. Пусть комбинационная схема задана таблицей истинности (табл. 7).

Таблица 7 - Таблица истинности функции трех аргументов для двух ФАЛ

Номер состояния	с	b	a	Z1	Z2
				~
				~

Так как значения Z₁, в 5 и 7 состояниях неопределены (безразличны), то функция Z1, может быть задана в виде:

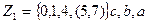
или

.

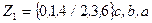Поскольку значения Z₁ в 5 и 7 состояниях безразличны, то мы можем считать их равными 0 или 1 так, чтобы максимально упростить схему. Следовательно, аналитическая запись для Z₁ может быть следующей:

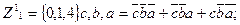
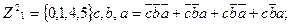
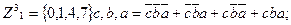
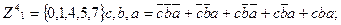
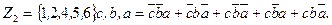
В дальнейшем можно минимизировать каждую функцию известными методами и построить комбинационную схему путем синтеза двух разделенных цепей, реализующих приведенные функции Z₁ и Z₂.

Однако применение такого способа при синтезе комбинационных схем с несколькими выходами может быть не рациональным, поскольку, если даже каждая из цепей будет построена минимальным образом, в целом логическое устройство может оказаться не минимальным.

Принцип получения минимальной схемы сводится к нахождению минимального набора членов с минимальным количеством букв, достаточного для описания всех формируемых данным устройством функций.

Рассмотрим метод построения минимальной комбинационной схемы с тремя выходами, способ функционирования которой задан табл. 8.

Таблица 8 - Истинность для трех ФАЛ

x1
x2
x3
Z1
Z2
Z3

Порядок минимизации следующий:

1. Записываем в табл. 9 наборы аргументов, на которых хотя бы одна функция принимает значение 1. В правой части таблицы указываются сами функции.

Таблица 9 - Члены СДНФ функций

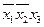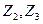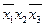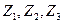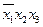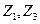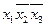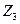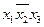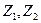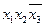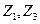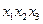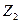2. Проводим операции склеивания членов табл. 9 и полученные результаты записываем в табл. 10 вместе с номерами функций, общими для склеиваемых пар. Склеиваемые комбинации аргументов в табл. 9 перечеркиваются.

Таблица 10 - Результаты операций склеивания

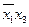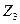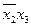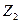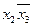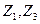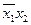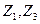Продолжение таблицы 10

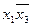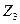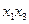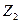Не проводятся операции склеивания над членами, не имеющими общих функций.

3. Составляется импликантная таблица (табл. 11) и проводятся операции поглощения членов функций импликантами. Результаты отмечаются в таблице (табл. 11).

Таблица 11 - Импликантная матрица

Импликанты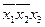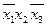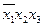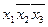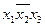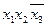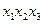

Z2

Z3

Z1

Z2

Z3

Z1

Z3

Z3

Z1

Z2

Z1

Z3

Z2

×

×

×

×

×

×

×

×

×

×

×

×

×

×

×

×

×

×

×

×

×

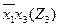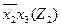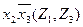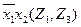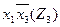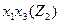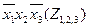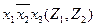4. Определяется набор импликант, обеспечивающих перекрытие всех столбцов табл. 11, и записываем их в табл. 12 вместе с номерами функций, перекрываемых импликантами.

Таблица 12 - Таблица импликант и функций

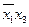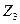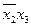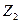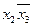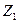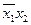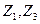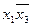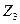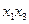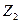Продолжение таблицы 12

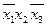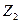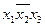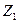5. Записываем выражения для выходов комбинационной схемы:

.

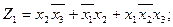
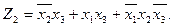
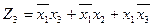Комбинационная схема, составленная на релейно-контактных элементах и реализующая приведенные функции, показана на рисунке 23.

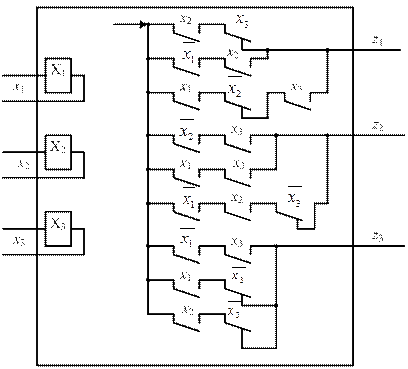
Рисунок 23 – Реализация комбинационной схемы на релейно-контактных элементах

Не представляет труда синтез комбинационного устройства в базисе {И, ИЛИ, НЕ}.

Для того чтобы реализовать полученные функции в базисе {ИЛИ, НЕ}, необходимо дважды проинвертировать каждый член выражений и тогда получим:

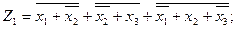
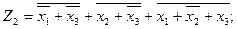
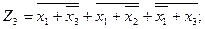
Проинвертировав дважды выражения для Z, мы получим функции, реализовать которые будет удобно в базисе {И, НЕ):