Примеры выполнения заданий

Г.А. Аршинов, В.Н. Лаптев, В.Г. Аршинов

Практикум

По математике

для студентов юридического факультета

Краснодар-2014

УДК 519 (075.8)

ББК 32.973.3

А20

Рецензенты:

Доктор технических наук В.В. Степанов – профессор факультета компьютерных технологий и автоматизированных систем Кубанского государственного технологического университета.

Доктор экономических наук, профессор Е.В. Луценко – профессор кафедры компьютерных технологий и систем Кубанского государственного аграрного университета.

А20 Аршинов Г.А., Лаптев В.Н., Аршинов В.Г. Практикум по математике. – Краснодар: ФГБОУ ВПО «Кубанский государственный аграрный университет», 2014. – с.

В учебном пособии предлагаются задания для проведения практических занятий по теории множеств, комбинаторики, теории графов и алгоритмов. Учебное пособие подготовлено в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования для специальности 030900 «Юриспруденция»

ISBN 978-5-94672-308-4

ã Аршинов Г. А., Лаптев В.Н., Аршинов В.Г. 2014.

ã Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Кубанский государственный аграрный университет», 2014.

Практическое занятие №1. Операции над множествами

Цель занятия:	1.	изучить способы задания множеств;
	2.	получить навыки в применении операций над множествами.

Множества можно задавать двумя способами:

Перечислением элементов множества.

Например, множество M={x, y, z}. Оно состоит из трёх элементов (порядок элементов произвольный), т.е. {x, y, z}={y, x, z}

описанием элементов множеств:

- описанием характеристических свойств, объединяющих элементы в виде уравнений, диаграмм Эйлера-Венна и геометрически.

Например, множество M = {x²Î N; x – простое число} задано квадратами простых чисел.

- описанием множеств, порожденных процедурами над элементами. Это означает указание алгоритма порождения элементов этого множества.

Например, подмножество М всех нечетных натуральных чисел с помощью порождающей процедуры имеет вид:

M={xÎN: x=1+2n, nÎN}

Операции над множествами

Рассмотрим операции над множествами в порядке убывания приоритета. Пересечением (произведением) двух множеств называется множество С, состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно. Обозначение: С = АìüВ	A∩B
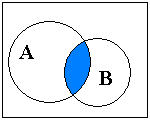Объединением (суммой) двух множеств А и В называется множество С, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В (или тому и другому вместе). Обозначение: С =АîþВ	AUB
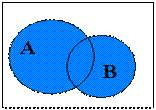Разностью множеств А и В называется такое множество С, которое состоит из тех и только тех элементов, которые принадлежат множеству А, но не принадлежат множеству В. Обозначение: С =А ½ В или С =А \ В	А\B
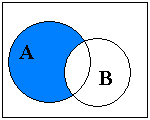Дополнением множества А до универсального множества U называется множество С, равное разности U½A. Обозначение: С = U½А или С = 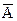Симметрической разностью двух множеств А и В называется множество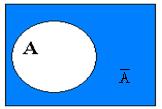
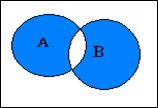
С = Аîþ В | Аìü В. Обозначение: С =А D В Формула включений и исключений для двух множеств А и В: n(АîþВ)= n(А)+ n(В) - n(А∩В). для трех множеств А, В и С:	А D В

n(АîþВîþС)= n(А)+n(В)+n(С)-n(А∩В)-n(А∩С)-n(В∩С)-n(А∩В∩С)

где n(Z) – количество элементов множества Z, т.е. его мощность.

Примеры выполнения заданий

1. Заданы множества: А = {1, 3, 5, 7, 9}, B = {1, 2, 3, 4, 5}.

Найдите элементы множеств: D = Аîþ В и Е = АìüВ.

D= {1, 2, 3, 4, 5, 6, 7 ,8, 9}, Е = {1, 3, 5}.