Отношения между суждениями по логическому квадрату.

Несравнимыми среди простых суждений являются суждения, имеющие различные субъекты или предикаты. Сравнимыми являются суждения с одинаковыми субъектами и предикатами.
Для иллюстрации отношений между простыми суждениями используется логический квадрат.

Среди сравнимых различают совместимые суждения, которые могут быть одновременно истинными, и несовместимые суждения, которые одновременно истинными быть не могут.
Совместимость бывает трех видов: полная совместимость (эквивалентность); подчинение; частичная совместимость (субконтрарность). Несовместимость бывает двух видов: противоположность (контрарность) и противоречивость (контрадикторность).
I. Отношением подчинения связаны суждения А и I, Е и О. Общие суждения (А и Е) являются подчиняющими, а частные (I, О) подчиненными. Для суждений находящихся в отношении подчинения, имеет значение условие истинности: Если истинно А(Е), то истинно и I(O), но не наоборот.
II. Отношением противоречия связаны суждения Е и I, А и О. Два противоречивых суждения (согласно законам логики) не могут быть одновременно ни истинными, ни ложными Если А - истинно, то О - ложно
Если А - ложно, то О - истинно
Если О - истинно, то А - ложно
Если О - ложно, то А - истинно
Если Е - истинно, то I - ложно
Если Е - ложно, то I - истинно
Если I -истинно, то E - ложно
Если I - ложно, то E - истинно
III. Отношением контрарности (противоположности) связаны только общие суждение А и Е. Закон исключения третьего к таким суждениям не применим. А и Е могут оказаться одновременно ложными, но не могут быть одновременно истинными (пример: оба суждения "Все любят логику" и "никто не любит логику" - ложны).
V. Отношение субконтрарности существует между частными суждениями I и О. I и О могут быть одновременно истинными, но не могут быть одновременно ложными (пример: оба суждения "Некоторые люди любят логику" и "некоторые люди не любят логику" - истинны).

24. Сложное суждение. Логические союзы и их семантика.

Сложные суждения — суждения, составными частями которых являются простые суждения или их сочетания. Сложное суждение может рассматриваться как образование из нескольких исходных суждений, соединенных в рамках данного сложного суждения логическими союзами (связками). От того, при помощи какого союза связываются простые суждения, зависит логическая особенность сложного суждения. Состав сложного суждения: В зависимости от способа образования различают конъюнктивные, дизъюнктивные, импликационные, эквивалентные и отрицательные суждения.

1.Дизъюнктивные суждения образуются с помощью разделительных (дизъюнктивных) логических связок (аналогичных союзу «или»). Подобно простым разделительным суждениям, они бывают:а)нестрогими (нестрогая дизъюнкция), члены которой допускают совместное сосуществование («то ли…, то ли…»). Записывается как ;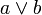

б)строгими (строгая дизъюнкция), члены которой исключают друг друга (либо одно, либо другое). Записывается как .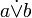

2.Импликационные суждения образуются с помощью импликации, (эквивалентно союзу «если …, то»). Записывается как 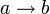или ab. В естественном языке союз «если …, то» иногда является синонимом союза «а» («Погода изменилась и, если вчера было пасмурно, то сегодня не одной тучи») и, в таком случае, означает конъюнкцию.3.Конъюнктивные суждения образуются с помощью логических связок сочетания или конъюнкции(эквивалентно запятой или союзам «и», «а», «но», «да», «хотя», «который», «зато» и другим). Записывается как 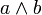.4.Эквивалентные суждения указывают на тождественность частей суждения друг другу (проводят между ними знак равенства). Помимо определений, поясняющих какой-либо термин, могут быть представлены суждениями, соединенными союзами «если только», «необходимо», «достаточно» (например: «Чтобы число делилось на 3, достаточно, чтобы сумма цифр, его составляющих, делилась на 3»). Записывается как 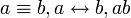(у разных математиков по-разному, хотя математический знак тождества всё-таки ).5.Отрицательные суждения строятся с помощью связок отрицания «не». Записываются либо как a ~ b, либо как a b (при внутреннем отрицании типа «машина не роскошь»), а также с помощью черты над всем суждением при внешнем отрицании (опровержении): «не верно, что …» (a b).