Примеры бинарных отношений. 8 страница
Важнейшая особенность булевых функций состоит в том, что они, как и их аргументы, принимают свои значения из двухэлементного множества  , т.е. характеризуются одним из двух возможных состояний.
, т.е. характеризуются одним из двух возможных состояний.
Пример.
В вычислительной технике булевы функции применяются для описания алгоритмов, средств вычислительной техники – дискретных устройств. Дискретные устройства предназначаются для преобразования дискретной информации, разлагающейся на элементарные единицы – биты. Биты в устройствах реализуются сигналами, которые описываются двоичными переменными – булевыми.
Определение.
Совокупность конкретных значений аргументов булевой функции называется кортежем, двоичным словом (  -словом) или булевым набором длины
-словом) или булевым набором длины  и обозначается как
и обозначается как 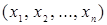 . Для булевой функции
. Для булевой функции 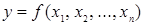 конкретное (индивидуальное) значение булевого набора
конкретное (индивидуальное) значение булевого набора 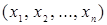 называется также интерпретацией булевой функцииf.
называется также интерпретацией булевой функцииf.
Пример.Для булевой функции 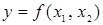 кортежами являются следующие совокупности конкретных значений аргументов:
кортежами являются следующие совокупности конкретных значений аргументов: 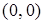 ,
, 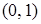 ,
, 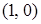 ,
, 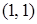 ; для булевой функции
; для булевой функции 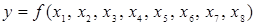 кортежами являются:
кортежами являются: 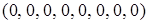 ,
, 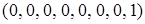 ,
, 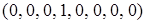 ,
, 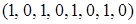 и т.д.
и т.д.
6.3 Область определения и область значений булевой функции
Определение.
Множество всех двоичных слов, обозначаемое как  , называется n-мерным булевым кубом и содержит
, называется n-мерным булевым кубом и содержит  элементов-слов, т.е.
элементов-слов, т.е.  .
.
Пример.
В множество двоичных слов для булевой функции 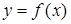 входит
входит 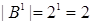 слова: (0) и (1); в множество двоичных слов для булевой функции
слова: (0) и (1); в множество двоичных слов для булевой функции 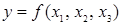 входит
входит 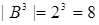 слов:
слов: 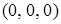 ,
, 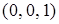 ,
, 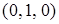 ,
, 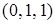 ,
, 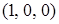 ,
, 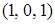 ,
, 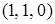 ,
, 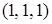 .
.
Определение.
Областью определения булевой функции от  -переменных служит множество слов длины
-переменных служит множество слов длины  , которые представляют собой всевозможные наборы из
, которые представляют собой всевозможные наборы из  двоичных цифр и их общее количество равно
двоичных цифр и их общее количество равно 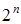 .
.
Определение.
Функция, зависящая от  аргументов, является полностью определенной, если указаны её значения для всех наборов (кортежей, слов) значений элементов.
аргументов, является полностью определенной, если указаны её значения для всех наборов (кортежей, слов) значений элементов.
Пример.
Булева функция от двух элементов является полностью определенной, если указаны её значения для каждого из четырех возможных наборов ( 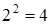 ), функция трех аргументов – на 8 (
), функция трех аргументов – на 8 ( 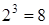 ) наборах также будет полностью определенной.
) наборах также будет полностью определенной.
Теорема 6.1
Число всех функций, зависящих от  переменных
переменных 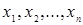 , равно
, равно 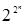 .
.
Действительно, булева функция  аргументов определена на
аргументов определена на 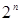 наборах, на которых она может принимать «0» или «1» из общего количества
наборах, на которых она может принимать «0» или «1» из общего количества 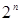 . Поэтому в соответствие каждой булевой функции можно поставить
. Поэтому в соответствие каждой булевой функции можно поставить 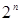 -разрядное двоичное число. Но количество различных
-разрядное двоичное число. Но количество различных 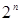 -разрядных чисел равно
-разрядных чисел равно 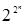 , а следовательно и количество различных булевых функций равно
, а следовательно и количество различных булевых функций равно 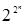 .
.
Пример.От двух аргументов 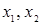 существует 16 булевых функций, т.е.
существует 16 булевых функций, т.е. 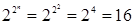 ; от трех – 256 (
; от трех – 256 ( 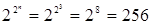 ), от четырех – 65536 функций (
), от четырех – 65536 функций ( 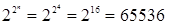 ).
).
6.4 Способы задания булевых функций
Существует четыре способа задания булевой функции:
- вербальный (словесный);
- табличный (с помощью таблицы истинности);
- порядковым номером, который имеет функция;
- аналитический (в виде формулы).
Задание булевых функций при помощи таблиц. Булевы функции можно задавать с помощью таблиц, подобных таблицам сложения и умножения одноразрядных чисел. В левой части такой таблицы перечисляются все  наборов значений переменных (булевых наборов длины
наборов значений переменных (булевых наборов длины  ), а в правой части − значения функций на этих наборах. Этот способ задания универсален, т.е. пригоден для любой функции, однако громоздок, поэтому применяется для задания функции небольшого числа переменных.
), а в правой части − значения функций на этих наборах. Этот способ задания универсален, т.е. пригоден для любой функции, однако громоздок, поэтому применяется для задания функции небольшого числа переменных.
Определение.
Таблицы, в которых каждой интерпретации (то есть набору аргументов) функции поставлено в соответствие её значение, называются таблицами истинности (соответствия) булевой функции.
В таблице истинности каждой переменной 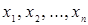 и значению самой функции
и значению самой функции 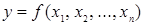 соответствует по одному столбцу, а каждой интерпретации - по одной строке. Интерпретации расположены в определенном порядке − лексикографическом, который совпадает с порядком возрастания наборов, рассматриваемых как двоичные числа.
соответствует по одному столбцу, а каждой интерпретации - по одной строке. Интерпретации расположены в определенном порядке − лексикографическом, который совпадает с порядком возрастания наборов, рассматриваемых как двоичные числа.
Пример.
Таблица истинности функции 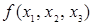 может иметь следующий вид (табл. 6.1).
может иметь следующий вид (табл. 6.1).
Таблица 6.1 – Пример таблицы истинности функции 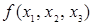
 | 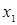 | 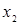 | 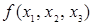 |
В столбцах 1, 2, 3 даны все возможные кортежи значений трех аргументов, т.е. сочетание нулевых и единичных значений трех аргументов. В столбце 4 – значения функции 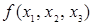 .
.
Рассмотрим булевы функции, которые зависят от одной и двух переменных.
Булевы функции, которые зависят от одной переменной, приведены в табл. 6.2 (их количество равно 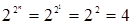 ).
).
Таблица 6.2 - Таблица истинности для булевых функций одной переменной
 | 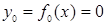 | 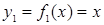 | 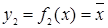 | 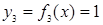 |
Две функции 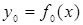 и
и 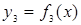 представляют собой функции-константы:
представляют собой функции-константы:
- 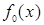 - является абсолютно ложной (константа нуля);
- является абсолютно ложной (константа нуля);
- 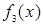 - является абсолютно истинной (константа единицы).
- является абсолютно истинной (константа единицы).
Функция 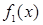 (функция повторения аргумента) повторяет значения переменной
(функция повторения аргумента) повторяет значения переменной  и поэтому просто совпадает с ней. Функция
и поэтому просто совпадает с ней. Функция 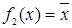 , называемая отрицанием или инверсией (
, называемая отрицанием или инверсией (  читается «не
читается «не  »), является единственной нетривиальной функцией. Она равна 1, когда аргумент принимает значение 0, и равна 0 при аргументе 1.
»), является единственной нетривиальной функцией. Она равна 1, когда аргумент принимает значение 0, и равна 0 при аргументе 1.
Всевозможные булевы функции двух переменных 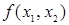 представлены в табл. 6.3 (их количество равно
представлены в табл. 6.3 (их количество равно 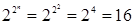 ).
).
Таблица 6.3 - Таблица истинности для булевых функций двух переменных
 |  |  |  |  | 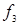 | 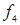 | 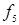 | 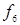 | 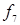 | 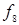 | 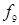 | 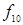 | 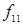 | 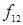 | 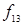 | 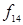 | 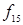 |
В табл. 6.4 приведена характеристика булевых функций двух переменных.
Таблица 6.4 - Характеристика булевых функций двух переменных
| Функ-ция | Обозначения (другие обозначения) | Названия | Чтение |
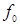 | Константа 0 (тождественный нуль, всегда ложно) | Константа 0 (Любое 0) | |
 | 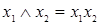 ( ( 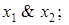 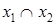 ) (AND, И) ) (AND, И) | Конъюнкция (произведение, пересечение, логическое «и») | 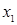 и и 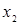 (и (и 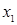 и и 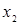 ). Истинна тогда, когда истинны обе переменные ). Истинна тогда, когда истинны обе переменные |
 | 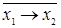 ( ( 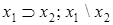 ) (>) ) (>) | Отрицание импликации (запрет) |  , но не , но не  |
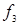 |  | Повторение (утверждение) первого аргумента | Как 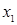 |
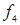 | 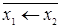 ( ( 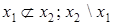 ) ) | Отрицание обратной импликации | Не  , но , но  |
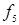 |  | Повторение второго аргумента | Как  |
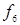 |  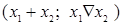 ( ( 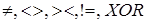 ) ) | Сумма по модулю 2 (неравнозначность, антиэквивалетность) |  не как не как  (или (или 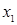 или или 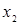 ). Истинна, когда истинны или ). Истинна, когда истинны или  , или , или  в отдельности в отдельности |
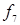 | 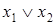 ( ( 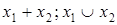 ) (OR, ИЛИ) ) (OR, ИЛИ) | Дизъюнкция (логическая сумма, логическое «или») | 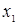 или или 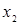 ( (  или хотя бы или хотя бы  ). Истинна тогда, когда истинны или ). Истинна тогда, когда истинны или  , или , или  , или обе переменные , или обе переменные |
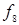 |  ( ( 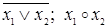 ) ) | Стрелка Пирса (функция Вебба, отрицание дизъюнкции) | Не  и не и не  . Истинна только тогда, когда . Истинна только тогда, когда  и и  ложны ложны |
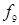 |  ( ( 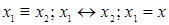 ) (Eqv) ) (Eqv) | Эквиваленция (равнозначность, эквивалентность) | 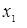 как как 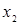 ( (  , если, и только если , если, и только если  ) ) |
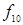 |  ( ( 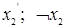 ) ) | Отрицание (инверсия) второго аргумента | Не  |
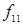 | 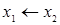 ( ( 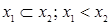 ) ) | Обратная импликация (обратное разделение с запретом) | Если  , то , то  ( (  или не или не  ) ) |
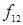 |  ( ( 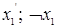 ) ) | Отрицание (инверсия) первого аргумента | Не  |
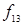 |  ( ( 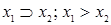 ) (Imp) ) (Imp) | Импликация (следование, селекция) | Если  , то , то  (не (не  или или  ). Ложна тогда и только тогда, когда ). Ложна тогда и только тогда, когда  истинна и истинна и  ложна ложна |
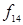 |  ( ( 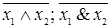 ) ) | Штрих Шеффера (отрицание конъюнкции, несовместимость, логическое «не-и») | Не  или не или не  . Ложна только тогда, когда . Ложна только тогда, когда  и и  истинны истинны |
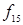 | Константа 1 (тождественная единица, всегда истинно) | Константа 1 (Любое 1) |
Шесть из приведенных функций не зависят от  или
или  (или от обоих вместе). Это две константы (
(или от обоих вместе). Это две константы ( 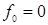 и
и 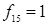 ), повторения (
), повторения ( 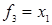 ,
, 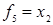 ) и отрицания (
) и отрицания ( 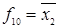 и
и 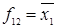 ), являющиеся функциями одной переменной (
), являющиеся функциями одной переменной ( 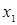 или
или  .) Из остальных десяти функций две (
.) Из остальных десяти функций две ( 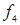 и
и 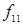 ) отличаются от соответствующих им (
) отличаются от соответствующих им (  и
и 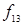 ) лишь порядком расположения элементов и поэтому не являются самостоятельными. Поэтому из 16 функций двух переменных только восемь являются оригинальными (
) лишь порядком расположения элементов и поэтому не являются самостоятельными. Поэтому из 16 функций двух переменных только восемь являются оригинальными ( 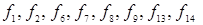 ).
).
В математической логике часто употребляются так называемые элементарные функции, которые играют такую же важную роль, как, например, 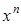 или
или  в математическом анализе. Элементарные логические функции –6это одноместные и двухместные логические функции.
в математическом анализе. Элементарные логические функции –6это одноместные и двухместные логические функции.
Примеры элементарных функций одной переменной приведены в табл. 6.2.
Примеры элементарных функций двух переменных представлены в табл. 6.3 и 6.4, это: отрицание 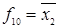 (
( 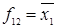 ); дизъюнкция
); дизъюнкция 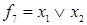 ; конъюнкция
; конъюнкция 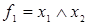 ; импликация
; импликация 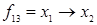 ; эквивалентность
; эквивалентность 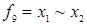 ; сумма по модулю 2
; сумма по модулю 2 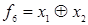 ; штрих Шеффера
; штрих Шеффера 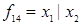 ; стрелка Пирса
; стрелка Пирса 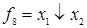 .
.
