Язык классической логики предикатов

В язык логики предикатов входят уже знакомые нам дескриптивные, логические и технические символы, что может быть выражено схемой (рис. 15):

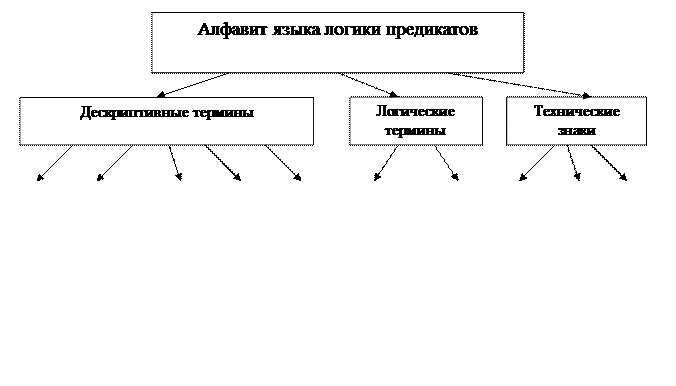
Рис. 15

Нелогическими символами языка логики предикатов являются:

1) предметные (индивидные) постоянные, являющиеся параметрами имён естественного языка. Для обозначения предметных постоянных используют, например, первые строчные буквы латинского алфавита (a, b, c, d и т. д.); 2) N-местные предметно-функциональные постоянные, являющиеся параметрами n-местных функторов естественного языка (для обозначения предметно-функциональных постоянных используют, например, следующие строчные буквы латинского алфавита (fⁿ, gⁿ, hⁿ и т. д., где верхний индекс указывает на местность постоянной); 3) N-местные предикаторные постоянные, являющиеся параметрами предикаторов естественного языка (для обозначения предметно-функциональных постоянных используют, например, следующие прописные буквы латинского алфавита: Pⁿ, Qⁿ, Rⁿ, Sⁿи т. д., где верхний индекс указывает на местность предикатора); 4) предметные (индивидные) переменные, принимающие различные значения из множества индивидов, к которым относятся утверждения в рамках определённого контекста (акие переменные, обозначаемые, например, x, y, z и т. д., необходимы для формальной записи выражений, содержащих кванторы существования и общности); 5) символы пропозициональных переменных (A, B, C, D и т. д.), которыми обозначаются записываемые посредством предыдущих символов простые или сложные суждения. Логическими символами языка логики предикатов являются: 1) пропозициональные связки; 2) кванторы. Техническими символами языка логики предикатов являются: 1) левая скобка, 2) правая скобка, 3) запятая.

§9.3. Запись имён и высказываний на ЯКЛП: термы и формулы

Поскольку все слова и словосочетания естественного языка являются именами или высказываниями, то в результате осуществления правильной записи на языке логики предикатов имён имеют место такие выражения этого языка, как термы, а в результате записи высказываний — формулы. Термом являются только предметные постоянные, предметные переменные, выражения fⁿ (t₁, t₂, …, t_n), где fⁿ — предметно-функциональная постоянная и t₁, t₂, …, t_n — термы.

V Пример

Запись на ЯКЛП простого имени «человек» осуществляется посредством символа предметной постоянной, допустим, а. Запись сложного имени «отец человека» осуществляется посредством сочетания символов предметно-функциональной и предметной постоянных, например, f¹(а). Если же имя «Иванов» выразим термом а, имя «Петров» — термомb, имя «отец Иванова» — термомf¹(а), имя «мать Петрова» — термом g¹(b), имя «день рождения отца Иванова» — термомh¹(f¹(а)), имя «день рождения матери Петрова» — термомh¹(g¹(b)), то запись такого сложного имени как «время от дня рождения отца Иванова до дня рождения матери Петрова» есть термI²((h¹(f¹(а)), h¹(g¹(b))).

Формулами языка логики предикатов являются только символы пропозициональных переменных (например, А,Ви т. д.), выражения Pⁿ (t₁, t₂, …, t_n), где Pⁿ — предметно-функциональная постоянная и t₁, t₂, …, t_n — термы, выражения ØА,(АÙВ), (АÚВ), (АÉВ),(АºВ),"xА,$xА и т. п.., где А иВ— формулы и x — предметная переменная.

V Пример

Высказывание «Земля — планета» записывается в виде формулы P¹(a), где P¹ — одноместная предикаторная постоянная (соответствующая свойству «являющийся планетой»), а— предметная постоянная (соответствующая имени «Земля»). Высказывание «Столица Бирмы существует» записывается в виде формулы Q¹(f¹(b)), где Q¹ — одноместная предикаторная постоянная (соответствующая свойству «являющийся существующим»), b — предметная постоянная (соответствующая имени «Бирма»), f¹ — предметно-функциональная постоянная (соответствующая предметной функции «быть столицей»), f¹(а)— «столица Бирмы». Высказывание «Столица России больше столицы Украины» — R²(f¹(a), f¹(b)) (R² — «больше»,a — «Россия», b — «Украина»,f¹ — «столица»); «Иванов любит Москву больше, чем столицу Индии» — S³(с,d,f¹(e)) (S³ — «любить больше, чем», c— «Иванов», d— «Москва», e— «Индия», f¹ — «столица»). Высказывание «Все являются существами» — "xP¹(x) (читается «Для всякого индивида верно, что он является существом», где x— «индивид», Q¹— «существо»); «Кто-то является человеком» — $yR¹(y)(читается «Существует индивид, такой, что он является человеком»). Содержащее два квантора высказывание «Каждый студент знает какую-нибудь историю» записывается формулой: "x(P¹(x)É$y(Q¹(y)ÙR²(x,y))) или "x$y(P¹(x)É(Q¹(y)ÙR²(x,y))) (читается «Для всякого индивида (человека) верно, что если он есть студент, то существует индивид, такой, что он есть история и является знаемым», где P¹ — «являющийся студентом», Q¹— «являющийся историей», R²— «…знает…»).

В последнем из приведённых примеров областью значений переменной x является множество студентов, т. е. она «пробегает» всё (в силу квантора общности) это множество. Областью значений переменной y является множество историй, взятое лишь в какой-то (в силу квантора существования) части. Причём все значения x находятся в отношении «являться знающими» со значениями y, пробегающего по части элементов множества историй. Таким образом, областью действия квантора " является исходная формула (P¹(x)É$y(Q¹(y)ÙR²(x,y))), которую можно записать символом пропозициональных переменных, допустим, А; соответственно, исходная формула может быть выражена формулой "xА. Областью действия квантора $ является формула (подформула) $y(Q¹(y)ÙR²(x,y)). Причём переменная x имеет в области действия квантора общности два вхождения (имеется в подформулах P¹(x) и R²(x,y)), переменная y имеет в области действия квантора существования также два вхождения (в подформулах Q¹(y) и R²(x, y)). Вхождением переменной в формулу логики предикатов называется каждый случай, когда в последовательности представляющих собой эту формулу знаков встречается данная переменная. Очевидно, что всякая предметная переменная, входящая в формулу логики предикатов, в структуре этой формулы может либо находиться непосредственно за квантором или в области действия квантора по этой переменной (т. е. быть связанной), либо не находиться непосредственно за квантором или в области действия квантора (т. е. быть свободной). Свободным вхождением предметной переменной в некоторую формулу называется тот случай, когда данная переменная не следует непосредственно за квантором или же находится вне области действия квантора по этой переменной.

V Пример

В формуле "x(P¹(x)ÉQ¹(x)) предметная переменная x, имеющая три вхождения, является связанной в каждом из них. В формуле $x(P²(x,y)ÙQ¹(y)) переменная x связана в каждом из двух случаев своего вхождения, а переменная y не связана в каждом из двух случаев своего вхождения.

Предметная переменная называется свободной в некоторой формуле, если имеется хотя бы одно её свободное вхождение в эту формулу, и связанной, если имеется хотя бы одно её связанное вхождение в эту формулу. Т. е. предметные переменные в формулах логики предикатов могут оказываться одновременно свободными и связанными. Соответственно, в формуле "x(P²(x,y)É$yQ¹(y)) одновременно свободной (в подформуле P²(x,y)) и связанной (в подформуле $yQ¹(y)) является предметная переменная y. Для обеспечения целей логического анализа результирующие термы первопорядкового языка логики предикатов не должны содержать в своём составе переменных (т. е. быть замкнутыми термами), соответственно, не должны содержать в своём составе свободных предметных переменных и формулы (т. е. быть замкнутыми формулами). Существуют следующие правила приписывания значений выражениям естественного языка, характерные для логики предикатов 1-го порядка:

1. Правила интерпретации — задания возможных значений предметных переменных и приписывания предметных значений предметным, предметно-функциональным и предикаторным постоянным той или иной формулы. Интерпретация начинается с выбора некоторого непустого множества индивидов (обозначим его символом « D »), которое называется областью интерпретации (универсумом рассуждения). В качестве такой области можно брать любое непустое множество, например, множество людей, чисел, планет и т. д.; возможно также объединение в одной области множеств различных предметов. Соответственно, нелогическим постоянным языка логики предикатов осуществляется приписывание значений в множестве D, т. е. задание особой семантической функции (обозначим её символом « I »), называемой интерпретационной. Задание I в каждом конкретном случае есть указание на то, какие именно значения должны быть приписаны исходным символам языка в составе рассматриваемых формул. Предметным постоянным (термам) приписываются в качестве предметных значений определённые предметы из D. Предикаторным постоянным приписываются некоторые свойства (в случае одноместности), а в случае многоместности — отношения. Предметным функторам в качестве предметного значения интерпретационная функция приписывает какую-нибудь n-местную предметную функцию, определённую на области D. Таким образом, чтобы осуществить процедуру интерпретации нелогических постоянных языка логики предикатов, необходимо выбрать некоторый универсум рассуждения D и функцию I, при этом пару <D,I> называют моделью классической логики предикатов. Модель классической логики предикатов — это любая пара <D,I>, в которой D — непустое множество, а I — интерпретационная функция. Приписывание значений предметным переменным происходит независимо от интерпретации нелогических постоянных, при этом каждой предметной переменной в качестве значения приписывается произвольный элемент множества D.

2. Правила приписывания истинностных значений интерпретированным формулам, не содержащим свободных переменных. Каждая интерпретированная формула есть определенное со стороны смысла и истинности высказывание, что осуществляется лишь при условии, если известны значения встречающихся в ней логических постоянных. При этом истинностное значение элементарного высказывания определяется в зависимости от заданных значений термов и предикаторной постоянной. Оно зависит от характера предметов в данной предметной области.

V Пример

Для формулы P²(f¹(x), f¹(y)) в качестве заданной интерпретации D предположим множество городов, в качестве P² — отношения «больше», в качестве f¹ —«быть столицей», в качестве x — Россию, y — Данию. Тогда вся формула представляет собой высказывание: «Столица России больше, чем столица Дании». Это высказывание истинно или ложно в зависимости от реального положения дел. Для сложных формул установление значения истинности аналогично установлению значения истинности сложных формул классической логики предикатов, поскольку определяющей истинностной функцией для них также являются пропозициональные связки. Например, если выраженное формулой "x(P¹(x)ÉQ¹(x)) высказывание истинно (допустим, что это истинное высказывание «Все львы являются хищниками»), то истинным является высказывание, выраженное формулой:

"x(P¹(x)ÉQ¹(x))É$x(P¹(x)ÙQ¹(x))

(т. е. истинным является высказывание, выражающее известное нам достоверное умозаключение «по логическому квадрату» от истинности общего суждения к истинности подчинённого ему частного суждения, а именно: «Поскольку верно, что все львы являются хищниками, то верно, что некоторые львы являются хищниками»).