Основные обозначения, понятия и факты логики высказываний
ТЕСТЫ
по основному курсу «Дискретная математика»
для специальности 010501 – «Прикладная математика и информатика»
и направления 510200 – «Прикладная математика и информатика»
Цикл общепрофессиональных дисциплин, федеральная компонента
Математический факультет КемГУ
Составитель: к.т.н., доцент кафедры АИТК
_______________ Гутова С.Г. «____»__________ 2008 г.
Зав. кафедрой АИТК,
д.т.н., профессор _________ Карташов В.Я. «___»___________2008 г.
Кемерово 2008
Основные обозначения, понятия и факты алгебры логики
Задание 1
Множество функций алгебры двузначной логики обозначается:
Задание 2
Количество двоичных векторов размерности 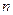 равно
равно
Задание 3
Количество логических функций двоичной логики от 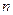 переменных равно
переменных равно
Задание 4
Функция 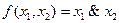 обозначает
обозначает
Задание 5
Функция 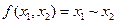 обозначает
обозначает
Задание 6
Функция 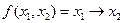 обозначает
обозначает
Задание 7
Функция 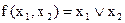 обозначает
обозначает
Задание 8
Нулевым набором значений аргументов функции из 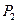 называется набор..
называется набор..
Задание 9
Единичным набором значений аргументов функции из 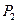 называется набор..
называется набор..
Представление логической функции таблицей
Задание 1
Вектор - столбец конъюнкции двух переменных имеет вид
Задание 2
Вектор - столбец дизъюнкции двух переменных имеет вид
Задание 3
Вектор - столбец импликации имеет вид
Задание 4
Вектор - столбец эквивалентности имеет вид
Задание 5
Вектор - столбец сложения по модулю 2 имеет вид
Задание 6
Вектор - столбец функции «штрих Шеффера» имеет вид
Задание 8
Вектор - столбец функции «стрелка Пирса» имеет вид
Основные свойства логических функций 2-х переменных
Задание 1
Конъюнкция равна единице тогда и только тогда, когда
Задание 2
Дизъюнкция равна единице тогда и только тогда, когда
Задание 3
Эквивалентность равна единице тогда и только тогда, когда
Задание 4
Сожжение по модулю 2 равно единице тогда и только тогда, когда
Задание 5
Импликация равна нулю тогда и только тогда, когда
Задание 6
Функция двух аргументов «штрих Шеффера» является
Задание 7
Отрицанием конъюнкции является
Задание 8
Отрицанием эквивалентности является
Задание 9
Отрицанием сложения по модулю 2 является
Задание 10
Отрицанием стрелки Пирса является
Задание 11
Отрицанием функции штрих Шеффера является
Основные эквивалентности
Задание 1
Закон поглощения имеет вид
Задание 2
Закон де Моргана имеет вид
Задание 3
Закон склеивания имеет вид
Задание 4
Закон исключенного третьего имеет вид
Задание 5
Булева формула эквивалентности х и у имеет вид
Задание 6
Булева формула сложения по модулю 2 х и у имеет вид
Задание 7
Булева формула импликации х и у имеет вид
05. Основные формулы логической функции из множества 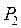
Задание 1
Разложение функции 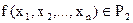 по переменной х1 имеет вид…
по переменной х1 имеет вид…
Задание 2
Дизъюнктивная нормальная форма функции 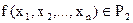 может иметь вид…
может иметь вид…
Задание 3
Конъюнктивная нормальная форма функции 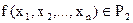 может иметь вид…
может иметь вид…
Задание 4
Полином Жегалкина функции 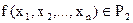 может иметь вид…
может иметь вид…
Задание 5
Булевыми операциями являются…
Задание 6
Операциями алгебры Жегалкина являются…
Задание 7
Полином Жегалкина функции 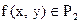 , такой что
, такой что 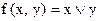 , имеет вид …
, имеет вид …
Задание 8
Полином Жегалкина функции 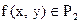 , такой что
, такой что 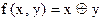 , имеет вид …
, имеет вид …
Задание 9
Полином Жегалкина функции 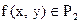 , такой что
, такой что 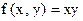 , имеет вид …
, имеет вид …
Задание 10
Полином Жегалкина функции 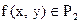 , такой что
, такой что 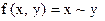 , имеет вид …
, имеет вид …
Задание 11
Полином Жегалкина функции 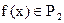 , такой что
, такой что 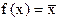 , имеет вид …
, имеет вид …
Задание 12
Совершенная дизъюнктивная нормальная форма функции 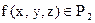 , заданной с помощью вектор-столбца f = (00100100)T имеет вид …
, заданной с помощью вектор-столбца f = (00100100)T имеет вид …
Задание 13
Совершенная дизъюнктивная нормальная форма функции 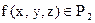 , заданной с помощью вектор-столбца f = (00000110)T имеет вид …
, заданной с помощью вектор-столбца f = (00000110)T имеет вид …
Задание 14
Совершенная дизъюнктивная нормальная форма функции 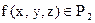 , заданной с помощью вектор-столбца f = (00010100)T имеет вид …
, заданной с помощью вектор-столбца f = (00010100)T имеет вид …
Задание 15
Совершенная дизъюнктивная нормальная форма функции 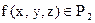 , заданной с помощью вектор-столбца f = (10000001)T имеет вид …
, заданной с помощью вектор-столбца f = (10000001)T имеет вид …
Задание 16
Совершенная конъюнктивная нормальная форма функции 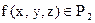 , заданной с помощью вектор-столбца f = (11101011)T имеет вид …
, заданной с помощью вектор-столбца f = (11101011)T имеет вид …
Задание 17
Совершенная конъюнктивная нормальная форма функции 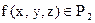 , заданной с помощью вектор-столбца f = (11010111)T имеет вид …
, заданной с помощью вектор-столбца f = (11010111)T имеет вид …
Задание 18
Совершенная конъюнктивная нормальная форма функции 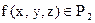 , заданной с помощью вектор-столбца f = (11111001)T имеет вид …
, заданной с помощью вектор-столбца f = (11111001)T имеет вид …
Задание 19
Совершенная конъюнктивная нормальная форма функции 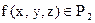 , заданной с помощью вектор-столбца f = (10011111)T имеет вид …
, заданной с помощью вектор-столбца f = (10011111)T имеет вид …
06. Предполные классы и функциональная полнота систем логических функций из множества 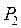
Задание 1
Функция 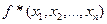 называется двойственной к
называется двойственной к 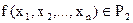 , если она может быть найдена по правилу:
, если она может быть найдена по правилу:
Задание 2
Функция 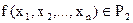 называется монотонной, если
называется монотонной, если
Задание 3
Функция 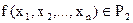 называется линейной, если её полином Жегалкина имеет вид
называется линейной, если её полином Жегалкина имеет вид
Задание 4
Функция 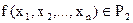 называется сохраняющей ноль, если для нее выполняется…
называется сохраняющей ноль, если для нее выполняется…
Задание 5
Функция 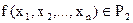 называется сохраняющей единицу, если для нее выполняется…
называется сохраняющей единицу, если для нее выполняется…
Задание 6
Функция 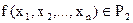 называется самодвойственной, если для нее выполняется…
называется самодвойственной, если для нее выполняется…
Задание 7
Для функции 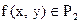 , имеющей вид
, имеющей вид 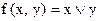 , двойственной является…
, двойственной является…
Задание 8
Для функции 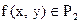 , имеющей вид
, имеющей вид 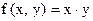 , двойственной является…
, двойственной является…
Задание 9
Для функции 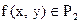 , имеющей вид
, имеющей вид 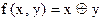 , двойственной является…
, двойственной является…
Задание 10
Для функции 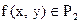 , имеющей вид
, имеющей вид 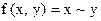 , двойственной является…
, двойственной является…
Задание 11
Для функции 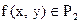 , имеющей вид
, имеющей вид 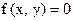 , двойственной является…
, двойственной является…
Задание 12
Для функции 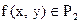 , имеющей вид
, имеющей вид 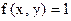 , двойственной является…
, двойственной является…
Задание 13
Согласно принципу двойственности, для 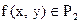 , булева формула которой
, булева формула которой 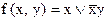 , двойственной является…
, двойственной является…
Задание 14
Согласно принципу двойственности, для 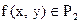 , булева формула которой
, булева формула которой 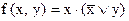 , двойственной является…
, двойственной является…
Задание 15
Для того, чтобы система функций из множества Р2 была функционально полна в сильном смысле, необходимо и достаточно, чтобы она содержала…
Основные обозначения, понятия и факты логики высказываний
Задание 1
Пусть высказывание А – «трава зеленая»; высказывание В – «роза имеет шипы». Тогда истинными будут высказывания…
а) «трава зеленая и роза имеет шипы»
б) «трава не зеленая или роза не имеет шипов»
в) «если трава зеленая, то роза имеет шипы»
г) «трава не зеленая и роза не имеет шипов»
д) «трава не зеленая тогда и только тогда, когда роза не имеет шипов»
Задание 2
Пусть высказывание А – «1 января – Новый Год»; высказывание В – «два меньше трех». Тогда истинными будут высказывания…
а) «если 1 января нет Нового Года, то два меньше трех»
б) «1 января – Новый Год тогда и только тогда, когда два больше или равно трем»
в) «1 января – Новый Год и два меньше трех»
г) «1 января – Новый Год и два не меньше трех»
д) «если 1 января нет Нового Года, то два больше или равно трем»
Задание 3
Пусть высказывание А – «пять – отличная оценка»; высказывание В – «роза имеет шипы». Тогда истинными будут высказывания…
а) «пять – отличная оценка и роза имеет шипы»
б) «пять –плохая оценка или роза не имеет шипов»
в) «если пять – отличная оценка, то роза имеет шипы»
г) «пять –плохая оценка и роза не имеет шипов»
д) «пять –плохая оценка тогда и только тогда, когда роза не имеет шипов»
Задание 4
Пусть высказывание А – «трава зеленая»; высказывание В – «два меньше трех». Тогда истинными будут высказывания…
а) «трава зеленая и два меньше трех»
б) «трава не зеленая или два не меньше трех»
в) «если трава зеленая, то два меньше трех»
г) «трава не зеленая и два больше или равно трем»
д) «трава не зеленая тогда и только тогда, два меньше трех»
Задание 5
Пусть высказывание А – «два меньше трех»; высказывание В – «роза имеет шипы». Тогда истинными будут высказывания…
а) «два меньше трех и роза имеет шипы»
б) «два не меньше трех или роза не имеет шипов»
в) «если два меньше трех, то роза имеет шипы»
г) «два не меньше трех и роза имеет шипы»
д) «два меньше трех тогда и только тогда, когда роза не имеет шипов»
