Логические операции над высказываниями

Операции над множествами.

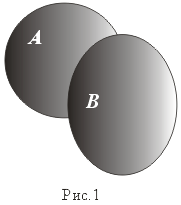
1. Объединение.
   (рис. 1)

C=A È B: = {x:x Î A или x Î B}

Пример 2. Решить неравенство

|2x+1| > 3.

Из данного неравенства следует либо неравенство

2x+1>3

в случае, когда 2x+1³ 0, тогда x>1, либо неравенство

2x+1<-3,

в случае, когда 2x+1<0, тогда x<-2.

Множеством решений исходного неравенства является объединение найденных промежутков решения (-¥,-2)È (1,+¥).

Пример 3. A = {1; 3; 5; 7; ...; 2n-1; ....} — нечетные числа

B = {2; 4; 6; 8; ....; 2n; ...} — четные числа

A È B = {1; 2; 3; ...; n; ......} — натуральный ряд

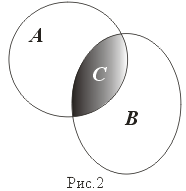
1. Пересечение.
   (рис. 2)

C=A Ç B:= {x: x Î A и x Î B }

Пример 4. A={2,4,...,2n,...}, B={3,6,9,...,3n,...}. Тогда C=AÇ B={6,12,...,6n,...}.

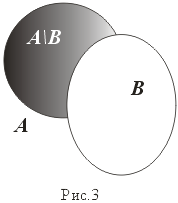
1. Вычитание.
   (рис. 3)

A \ B: = {x:x Î A и x Ï B}

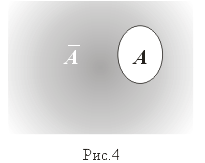
1. Дополнение.
   (рис.4)

Пусть U — универсальное множество ( все остальные множества принадлежат U)

A = CA: = {x:x Î U и x Ï A} = U \ A

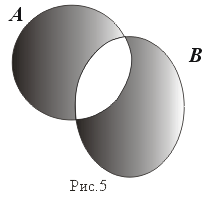
1. Симметрическая разность.
   (рис. 5)

A D B:= (A \ B) È (B \ A) = (A È B) \ (A Ç B)

Свойства операций над множествами.

Из определений объединения и пересечения множеств следует, что операции пересечения и объединения обладают следующими свойствами:

1. Коммутативность.

A È B=B È A
A Ç B=B Ç A

1. Ассоциативность.

(A È B) È C=A È (B È C)
(A Ç B) Ç C= A Ç (B Ç C)

1. Дистрибутивность.

(A È B) Ç C = (A Ç C) È (B Ç C)
(A Ç B) È C= (A È C) Ç (B È C)

1. A È A=A, A Ç A=A
   A È Æ = A, A Ç Æ= Æ
2. Законы де Моргана (законы двойственности).

1) A È B= A Ç B
2) A Ç B= A È B

3.Св-ва дополнений мно-во : расмотрим некоторые св-ва дополнений мно-в до основного пространства Омега.

Например Все плоские фигуры на плоскости, это подмножество плоскостей ,а плоскость будет основным множеством.

Декартова произведение мно-в: а принадлежит А, в принадлежит В, тогда пару элементов а и в можно записать (а; в) и это пора называется упарядочной парой.

Мно-во, элементами которого явл. все упорядочные пары (а;в) где элемент а принадлежит А, а в принадлежит В, называется декартовым произведениий мно-во.

4 .Высказывание – это всякое утверждение про которое можно сказать, что оно истина или ложно.

Логические операции над высказываниями

Отрицание.

Отрицанием высказывания х называется новое высказывание 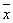, которое является истинным, если высказывание х ложно, и ложным, если высказывание х истинно.
Отрицание высказывания х обозначается 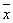и читается «не х» или «неверно, что х».
Логические значения высказывания 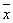можно описать с помощью таблицы.

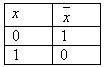
Таблицы такого вида принято называть таблицами истинности.
Пусть х высказывание. Так как 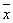также является высказыванием, то можно образовать отрицание высказывания 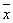, то есть высказывание 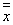, которое называется двойным отрицанием высказывания х. Ясно, что логические значения высказываний х и 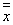совпадают.
Например, для высказывания «Путин президент России» отрицанием будет высказывание «Путин не президент России», а двойным отрицанием будет высказывание «Неверно, что Путин не президент России».

Конъюнкция.

Конъюнкцией (логическим умножением) двух высказываний х и у называется новое высказывание, которое считается истинным, если оба высказывания х и у истинны, и ложным, если хотя бы одно из них ложно.
Конъюнкция высказываний х и у обозначается символом х&у ( 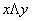, ху ) , читается «х и у» . Высказывания х и у называются членами конъюнкции.
Логические значения конъюнкции описываются следующей таблицей истинности:

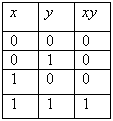
Например, для высказываний «6 делится на 2», «6 делится на 3» их конъюнкцией будет высказывание «6 делится на 2 и 6 делится на 3», которое, очевидно, истинно.
Из определения операции конъюнкции видно, что союз «и» в алгебре логики употребляется в том же смысле, что и в повседневной речи. Но в обычной речи не принято соединять союзом «и» два высказывания далеких друг от друга по содержанию, а в алгебре логики рассматривается конъюнкция двух любых высказываний.

Дизъюнкция

Дизъюнкцией (логическим сложением) двух высказываний х и у называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний х, у истинно, и ложным, если они оба ложны. Дизъюнкция высказываний х, у обозначается символом «x V у» , читается «х или у» . Высказывания х, у называются членами дизъюнкции.
Логические значения дизъюнкции описываются следующей таблицей истинности:

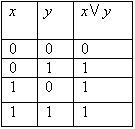
В повседневной речи союз «или» употребляется в различном смысле: исключающем и не исключающем. В алгебре логики союз «или» всегда употребляется в не исключающем смысле.

Импликация.

Импликацией двух высказываний х и у называется новое высказывание, которое считается ложным, если х истинно, а у - ложно, и истинным во всех остальных случаях.
Импликация высказываний х, у обозначается символом 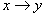, читается «если х, то у» или «из х следует у». Высказывание х называют условием или посылкой, высказывание у - следствием или заключением, высказывание 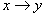следованием или импликацией.
Логические значения операции импликации описываются следующей таблицей истинности:

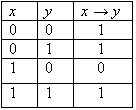
Употребление слов «если .... то ...» в алгебре логики отличается от употребления их в обыденной речи, где мы, как правило, считаем, что, если высказывание х ложно, то высказывание «Если х, то у» вообще не имеет смысла. Кроме того, строя предложение вида «если х, то у» в обыденной речи, мы всегда подразумеваем, что предложение у вытекает из предложения х . Употребление слов «если ..., то ...» в математической логике не требует этого, поскольку в ней смысл высказываний не рассматривается.
Импликация играет важную роль в математических доказательствах, так как многие теоремы формулируются в условной форме «Если х, то у». Если при этом известно, что х истинно и доказана истинность импликации 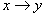, то мы вправе сделать вывод об истинности заключения у .

Эквивалентность.

Эквивалентностью двух высказываний х и у называется новое высказывание, которое считается истинным, когда оба высказывания х, у либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.
Эквивалентность высказываний х, у обозначается символом 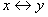, читается «для того, чтобы х, необходимо и достаточно, чтобы у» или «х тогда и только тогда, когда у». Высказывания х, у называются членами эквивалентности.
Логические значения операции эквивалентности описываются следующей таблицей истинности:

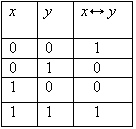
Эквивалентность играет важную роль в математических доказательствах. Известно, что значительное число теорем формулируется в форме необходимых и достаточных условий, то есть в форме эквивалентности. В этом случае, зная об истинности или ложности одного из двух членов эквивалентности и доказав истинность самой эквивалентности, мы зак­лючаем об истинности или ложности второго члена эквивалентности.

5.Алгоритмом составление табл. истености : раставить порядок действий 1)отрицание; 2)умножения; 3)сложение; 4)следование; 5)эквивалентность.

Порядок действий изменяется если имеются скобки .2)количество строк 2ⁿ, где n число аргументов .3)Число столбцов n+p; n-число аргументов; p-кол-во действий.4)Таблица истиности заполняется по столбцам, в которой указывается:1)аргументы, заполненые порядки возрастания числа двоичной системы счисления.2)Действий в соответствии с порядками и в соответствии с табл. истености для данной логической операции.

6. Две формулы алгебры логики А и В называется равносильными, если они принимают одинаковые логические значения при любом наборе значений аргументов входящие в формулы.

Между понятием равносильности и знаком эквивалентности сущ. связь : Если формулы а и в равносильны, то формула А Эквивалента В принимает значение 1 то есть истина при всех значениях аргумента.

7. _{1)А /\ В равносильна} В /\ А .- Коммутативный закон конъюнкции.

2)А \/ В равносильна В\/ А.- коммутативный закон дизъюнкции.

3)А /\(В /\ С)равносильна(А /\ В)/\ С.- ассоциативный закон конъюнкции.

4)А \/ (В\/С) равносильна (А\/В)\/С.- ассоциативность дизъ.

5)А/\(В\/С)равносильна(А/\В)\/(А\/С).- дистрибутивность конъюнкции, отрицательно дизъюнкции .

6)А\/(В/\С)равносильна (А\/В)/\(А\/С) .- дистрибутивность дизъюнкции относительно конъюнкции .

8) Теорема . Пусть А равносильно В а С произвольная формула тогда : А/\С равносильна В/\С

С/\А равносильна С/\В

А\/С равносильна В\/С

С\/А равносильна С\/В