Правило введения квантора существования
 позволяет заключить, что
позволяет заключить, что  является истинным, когда известен некоторый элемент
является истинным, когда известен некоторый элемент 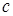 , для которого истинно
, для которого истинно  .
.
Правило  -введения
-введения
То же, что и правило связывания квантором общности или правило обобщения.
Правило  -введения
-введения
То же, что иправило связывания квантором существования
Правила вывода
Правила вывода позволяют получать новые формулы, которые являются истинными при условии истинности всех посылок, входящих в правило.
Правило обобщения
То же, что и правило связывания квантором общности или правило  -введения.
-введения.
Правило отделения
Правило отделения имеет следующий логический смысл: если посылка верна, то верно и следствие из неё.
Правило отделения в исчислении предикатов
Формулируется так же, как и в исчислении высказываний:  .
.
Правило переименования связанной переменной.
Связанную переменную формулы  можно заменить (в кванторе и во всех вхождениях в области действия квантора) другой переменной, не являющейся свободной в
можно заменить (в кванторе и во всех вхождениях в области действия квантора) другой переменной, не являющейся свободной в  .
.
Правило подстановки
Правило подстановки выражает тот факт, что если в тождественно истинной формуле все вхождения какого-либо атома заменить на некоторую формулу, то полученное выражение останется тождественно истинным.
Правило связывания квантором общности
 , где
, где  содержит свободные вхождения
содержит свободные вхождения  , а
, а  их не содержит.
их не содержит.
То же, что и правило обобщенияили правило  -введения.
-введения.
Правило связывания квантором существования
 , где
, где  содержит свободные вхождения
содержит свободные вхождения  , а
, а  их не содержит.
их не содержит.
То же, что иправило  -введения.
-введения.
Правило удаления квантора всеобщности
 , где
, где 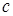 − произвольно выбранный элемент предметной области
− произвольно выбранный элемент предметной области 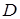 , в которой справедливо
, в которой справедливо  .
.
Правило удаления квантора существования
 в истинной формуле
в истинной формуле  заключается в указании имени элемента
заключается в указании имени элемента 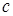 (конкретного или гипотетического), для которого
(конкретного или гипотетического), для которого  истинно.
истинно.
Правильно построенная формула(в логике высказываний)
В логике высказываний правильно построенная формула определяется рекурсивно следующим образом: атом есть формула; если  и
и  - формулы, то
- формулы, то  - также формулы; никаких формул, кроме порожденных указанными выше правилами, не существует.
- также формулы; никаких формул, кроме порожденных указанными выше правилами, не существует.
Правильно построенная формула логики предикатов
Рекурсивно определяется следующим образом: атом является формулой; если  и
и  − формулы, то
− формулы, то  также являются формулами; если
также являются формулами; если  − формула, а
− формула, а  − свободная переменная, то
− свободная переменная, то  и
и  тоже формулы; никаких формул, кроме порожденных указанными выше правилами, не существует.
тоже формулы; никаких формул, кроме порожденных указанными выше правилами, не существует.
Правильное рассуждение
Рассуждение, которое выражается тождественно истинной формулой.
