Закон исключенного третьего 8 страница

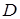2. Формула получает значение И, если получает значение И для каждого из , в противном случае она получает значение Л.

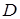3. Формула получает значение И, если получает значение И хотя бы для одного из , в противном случае она получает значение Л.

4. Формула, содержащая свободные переменные, не может получать истинностные значения.

Пример.Пусть задан предикат . Формула не истинна, если универсом (предметной областью) является множество целых чисел, однако она была бы истинной, если в качестве предметной области взять множество целых чисел, больших чем 2.

Квантифицированный предикат , где , не является истинным, если предметная область − множество целых чисел, потому что имеются значения из этой области (например, ) такие, что 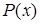ложно. Для истинности 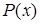должно быть истинным для каждого значения из предметной области.

Пример.Предикат , где , является истинным, если предметной областью есть множество действительных чисел, т.к. истинно для .

Предикат , где , также истинен, если предметной областью есть множество действительных чисел, однако, он не является истинным, если предметная область есть множество целых чисел, т.к. не существует целого числа, квадрат которого равен 5.

При логической (истинностной) интерпретации формул логики предикатов так же, как и в логике высказываний определяются общезначимые, противоречивые,выполнимые, необщезначимые формулы, а также логическое следствие.

12.4 Законы и тождества логики предикатов

Все законы и тождества, которые справедливы в логике высказываний, остаются справедливыми и в логике предикатов.

Для эквивалентных преобразований предикатных высказываний с кванторами дополнительно необходимо использовать приведенные ниже законы.

1. Замена связанной переменной:

;

,

− одноместный предикат.

Введение нового обозначения связанной переменной (т.е. переименование связанной переменной) не изменяет смысл формулы логики предикатов, если выполняется следующее условие: никакая свободная переменная в любой части формулы не должна после переименования оказаться связанной.

Пример.

Для нового обозначения связанной переменной следует выбирать букву, которая отсутствует в формуле, например, . Здесь осуществлена операция переименования связанной переменной .

2. Коммутативные свойства кванторов:

;

.

Менять местами можно только одноименные кванторы.

.

3. Дистрибутивные свойства кванторов:

;

;

;

,

где − формула логики предикатов, которая не содержит ;

;

.

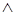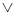Сформулированный дистрибутивный закон справедлив только для квантора всеобщности при конъюнкции и квантора существования при дизъюнкции , т.к. другие комбинации приводят к неравенствам:

;

.

Для преодоления данного ограничения дистрибутивного закона, следует использовать замену связанной переменной:

;

.

Таким образом, в общем случае дистрибутивные свойства кванторов можно записать следующей схемой:

;

,

где − любой из кванторов или .

4. Закон де Моргана для кванторов:

;

.

12.5 Предваренные нормальные формы

Определение.

Формула в логике первого порядка находится в предваренной нормальной форме (ПНФ) тогда и только тогда, когда она может быть представлена в виде , где каждое , , есть или , или , а − формула, не содержащая кванторов. Причем называется префиксом, а − матрицей формулы .

Для преобразования выражений произвольной формы в ПНФ необходимо поочередно выполнить следующие этапы преобразования:

1. Исключить логические связки эквиваленции и импликации, выразив их через операции дизъюнкции, конъюнкции и отрицания с помощью следующих законов: ; .

2. Опустить знаки операций отрицания непосредственно на предикаты, используя закон двойного отрицания и законы де Моргана , , в том числе для кванторов: ; .

3. Если необходимо, переименовать связанные переменные.

4. Вынести кванторы в начало формулы, используя соответствующие законы, для получения предваренной нормальной формы

Пример.

Приведем формулу к предваренной нормальной форме.

Сначала исключим импликацию, затем опустим знак операции отрицания непосредственно на предикат и вынесем квантор в начало:

.

12.6 Выводимость в логике предикатов

Для дедуктивного вывода в логике предикатов можно использовать правила, которые применяются для подобных выводов в логике высказываний. Однако в логике предикатов для проведения дедуктивных умозаключений используются также и специфические правила, учитывающие наличие кванторных операций. К таким правилом относятся следующие правила:

а) Правило удаления квантора всеобщности используется для доказательства истинности , где 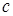− произвольно выбранный элемент предметной области 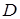, в которой справедливо .

Пример.

Из посылки «Все студенты любят получать хорошие оценки» делаем вывод: «Студент Петров любит получать хорошие оценки».

б) Правило введения квантора всеобщности утверждает истинность , если доказана истинность для любого 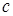, то есть для всех элементов 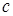из рассматриваемой предметной области .

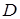в) Правило удаления квантора существования в истинной формуле заключается в указании имени элемента 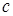(конкретного или гипотетического), для которого истинно.

г) Правило введения квантора существования позволяет заключить, что является истинным, когда известен некоторый элемент 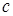, для которого истинно .

12.7 Контрольные вопросы и задания

1. Дайте определение понятия предикат.

2. Что называется порядком предиката?

3. Приведите примеры -местных предикатов.

4. Какие типы символов разрешается использовать для построения атомов логики предикатов?

5. Приведите примеры функциональных символов.

6. Дайте определение терма.

7. Что понимают под предметной областью?

8. Что понимают под квантором всеобщности?

9. Дайте определение понятию «квантор существования».

10. Какие переменные называются связанными, а какие – свободными?

11. Из чего состоит интерпретация формулы логики первого порядка?

12. Объясните суть замены связанной переменной.

13. Сформулируйте коммутативные свойства кванторов.

14. Запишите формулы закона де Моргана для кванторов.

15. Дайте определение предваренной нормальной формы.

16. С помощью каких законов можно опустить знаки операций отрицания непосредственно на предикаты?

17. Каким образом можно преобразовать выражения произвольной формы в ПНФ?

Лекция 13. Исчисление предикатов

13.1 Основные понятия исчисления предикатов

В логике предикатов, в отличие от логики высказываний, нет эффективного способа для распознавания общезначимости формул. Поэтому аксиоматический метод становится существенным при изучении формул, содержащих кванторы.

В логике предикатов существует формальная система, которая носит название исчисление предикатов. Выделение общезначимых формул в ней так же, как и в исчислении высказываний, осуществляется путем указания некоторой совокупности формул, которые называются аксиомами, и указания правил вывода, позволяющих из общезначимых формул получить общезначимые.

Определение.

Исчисление предикатов − это аксиоматическая теория, символами которой являются:

1) символы предметных переменных: ;

2) символы предикатов: , где ;

3) логические символы: ;

4) символы кванторов: ;

5) скобки и запятую: ),( .

13.2 Аксиомы исчисления предикатов

Аксиомами исчисления предикатов являются следующие аксиомы:

а) ;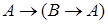

б) ;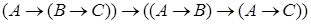

в) ;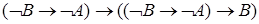

г) ;

д) .

13.3 Правила вывода в исчислении предикатов

В исчислении предикатов используются следующие правила вывода:

1. Правило отделения, которое формулируется так же, как и в исчислении высказываний: ;

2. Правило связывания квантором общности (правило обобщения, правило -введения) , где содержит свободные вхождения , а их не содержит.

3. Правило связывания квантором существования (правило -введения) , где содержит свободные вхождения , а их не содержит.

4. Правило переименования связанной переменной. Связанную переменную формулы можно заменить (в кванторе и во всех вхождениях в области действия квантора) другой переменной, не являющейся свободной в .

Пример.Докажем правило переименования связанных переменных для квантора общности:

1. (по условию).

2. (аксиома а) ).

3. (правило обобщения).

4. .

Понятия вывода, теоремы, вывода из системы гипотез определяется в исчислении предикатов, как и в любой аксиоматической теории.

Теорема 13.1(ослабленная теорема о дедукции)

Пусть − множество формул, 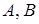− формулы и 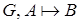, и существует вывод в исчислении предикатов, построенный с применением только правила отделения, то .

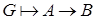Утверждение 1. Аксиомы исчисления предикатов − общезначимые формулы.

Утверждение 2. формула, получающаяся из общезначимой формулы по любому из правил 1 − 4, является общезначимой.

13.4 Контрольные вопросы и задания

1. Поясните понятие формальной системы, которая имеет название исчисление предикатов.

2. Сформулируйте назначение исчисления предикатов.

3. Запишите формулы аксиом исчисления предикатов.

4. Перечислите правила вывода, которые можно использовать для проведения дедуктивных умозаключений с высказываниями логики предикатов.

Лекция 14. Общие определения комбинаторики. Основные правила комбинаторики. Модели типовых комбинаторных конфигураций.

14.1 Общие определения комбинаторики. Понятие 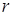-выборки. Общие задачи комбинаторики

На практике часто приходится выбирать из некоторого множества объектов подмножества элементов, обладающих теми или иными свойствами, располагать элементы одного или нескольких множеств в определенном порядке и т.д. Поскольку в таких задачах речь идет о тех или иных комбинациях объектов, их называют "комбинаторные задачи".

Комбинаторика занимается различного рода соединениями, которые можно образовать из элементов некоторого конечного множества. Термин "комбинаторика" происходит от латинского combina - сочетать, соединять.

Комбинаторикой называется раздел математики, изучающей вопрос о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).

Наиболее широкое применение комбинаторные задачи находят при решении задач теории вероятностей, также комбинаторика широко используется в теории графов и теории чисел. Как при решении задач с использованием комбинаторных конфигураций, так и в других ситуациях нам понадобятся некоторые формулы комбинаторики.

Определение. Пусть задано r множеств: , при этом ,тогда r-выборкой называется упорядоченная совокупность элементов вида .

Определение. Множество всех выборок 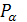называется теоретико-множественным произведением или произведением r множеств .Обозначается

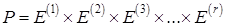
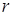-выборка не является множеством, а является элементом теоретико-множественного произведения.

В 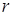-выборке каждый элемент (компонента) может повторяться, но их порядок фиксирован.

Определение. Две упорядоченные выборки равны или эквивалентны тогда и только тогда, когда соответствующие элементы равны .

Определение. r-выборка с произвольным порядком размещения компонент называется неупорядоченной r-выборкой. Обозначается .

Основными и типичными операциями и связанными с ними задачами комбинаторики являются:

1) образование упорядоченных множеств, состоящее в установлении определенного порядка следования элементов множества друг за другом, –

составление перестановок;

2) образование подмножеств, состоящее в выделении из данного множества некоторой части его элементов, – составление сочетаний;

3) образование упорядоченных подмножеств – составление размещений.

14.2 Основные правила комбинаторики

Большинство комбинаторных задач решается с помощью двух основных правил – правила суммы и правила произведения.

Правила суммы и произведения используются при вычислении количества различных комбинаций.

Правило суммы. Если и – несвязанные события, и существует возможных исходов события , и возможных исходов события , то возможное число исходов события « или » равно сумме .

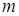Интерпретация. Если элемент можно выбрать способами, а элемент – способами, то выбор элемента можно осуществить способами. Пусть – попарно непересекающиеся множества, , где . Тогда, очевидно, выполняется равенство .

Правило произведения.Если дана последовательность событий с возможными исходами первого, – второго, и т.д., вплоть до возможных исходов последнего, то общее число исходов последовательности k событий равно произведению .

Правило произведения тоже можно сформулировать на языке теории множеств. Пусть обозначает множество исходов первого события, – множество исходов второго, и т. д. Тогда любую последовательность событий можно рассматривать как элемент декартова произведения , чья мощность равна .

Пример. Из 28 костей домино берутся 2 кости. В каком числе комбинаций вторая кость будет приложима к первой?