Система представителей отношения эквивалентности
Подмножество из множества  , содержащее по одному и только одному элементу из каждого класса некоторого разбиения множества.
, содержащее по одному и только одному элементу из каждого класса некоторого разбиения множества.
Соответствие
Если 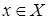 и
и 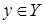 , то
, то  и
и  . В таких случаях
. В таких случаях  есть отношение от
есть отношение от  к
к  , называется соответствиеми обозначается
, называется соответствиеми обозначается  .
.
Сравнимые элементы
Элементы  и
и  называются сравнимыми в отношении частичного порядка
называются сравнимыми в отношении частичного порядка  , если выполняется хотя бы одно из соотношений
, если выполняется хотя бы одно из соотношений 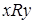 или
или 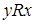 .
.
Схема отношения
Список атрибутов реляционной таблицы.
Сюръективное отображение
Функция 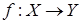 называется сюръективным отображением, если
называется сюръективным отображением, если 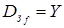 . Для сюръективной функции для любого
. Для сюръективной функции для любого 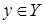 существует
существует 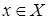 такой, что
такой, что 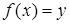 .
.
Сюръективная функция
То же, что и сюръективное отображение.
Тождественное отношение
Отношение, равносильное  .
.
Транзитивность
Отношение 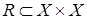 называется
называется  транзитивным, если
транзитивным, если 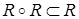 , т.е. из
, т.е. из 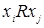 и
и 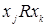 следует
следует 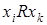 .
.
Унарное отношение
То же, что и одноместное отношение.
Универсальное отношение
То же, что и полное отношение.
Упорядоченное множество
Множество, в котором определено отношение порядка.
Фактор-множество
Множество всех сечений отношения  называется фактор-множеством множества
называется фактор-множеством множества  по отношению
по отношению  и обозначают
и обозначают  .
.
Функциональное отношение
Отношение 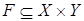 называется функциональным, если его элементы (упорядоченные пары
называется функциональным, если его элементы (упорядоченные пары 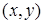 ) имеют различные первые координаты.
) имеют различные первые координаты.
Функция
То же, что и отображение
Цепь
То же, что и линейно упорядоченное множество.
Частично упорядоченное множество
Если на множестве задано отношение частичного порядка, то это множество называется частично упорядоченным.
Частичная функция
Если вместо 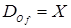 в функциональном отношении выполняется
в функциональном отношении выполняется 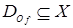 , то
, то  называется частичной функцией.
называется частичной функцией.
Основы математической логики
Двоичная логика. Булевы функции и преобразования
N-мерный булевый куб
Множество всех двоичных слов (обозначаемое как  ), содержит
), содержит  элементов-слов, т.е.
элементов-слов, т.е.  .
.
Алгебра Жегалкина
Алгебра  , образованная множеством
, образованная множеством  вместе с операциями конъюнкции (
вместе с операциями конъюнкции ( 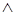 ), суммы по модулю 2 (
), суммы по модулю 2 ( 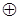 ) и константами 0 и 1.
) и константами 0 и 1.
Алгебра логики
Двухэлементная булева алгебра 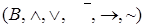 , где носитель алгебры
, где носитель алгебры 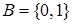 , и в которой множество операций дополнено двумя бинарными операциями: импликацией
, и в которой множество операций дополнено двумя бинарными операциями: импликацией 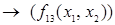 и эквивалентностью
и эквивалентностью 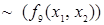 .
.
Булева алгебра (двухэлементная)
Алгебраическая структура 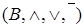 , где
, где 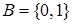 и операция
и операция 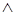 есть конъюнкция
есть конъюнкция 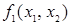 ,
, 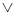 есть дизъюнкция
есть дизъюнкция 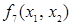 , «
, «  » есть отрицание
» есть отрицание 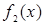 .
.
Булева функция
Функция вида 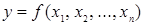 , аргументы
, аргументы 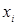 и значения
и значения  которой принадлежат множеству
которой принадлежат множеству  .
.
Булевы константы
Значения 0 и 1 из множества  .
.
Булевы переменные
Переменные, которые могут принимать значения только из множества  .
.
Булевый базис
Базис, состоящий из отрицания, дизъюнкции и конъюнкции.
Булевый набор
Совокупность конкретных значений аргументов булевой функции.
Двоичное слово (  -слово)
-слово)
Совокупность конкретных значений аргументов булевой функции.
Двойственная функция
Функция 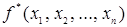 называется двойственной к функции
называется двойственной к функции 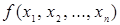 , если
, если 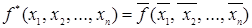 .
.
