Индивидуальное угадывание

Если организовать коллективного угадывания не удается, то прихо-дится довольствоваться вторым – индивидуальным угадыванием. В насто-ящее время для лингвистических нужд применяется два вида индивиду-ального угадывания:

– угадыванием по полной программе по схеме Шеннона-Пиотровского;

– угадыванием по сокращенной программе той же схемы.

Кроме того, для проверки достоверности, получаемых по этим програ-ммам обобщённых энтропийно-информационных характеристик текста ис-пользуются результаты угадывания букв текста, получаемые с помощью ме-тода Колмогорова (см. [107a]. Каждая из этих программ реализуется на одном испытуемым, являющимся носителем исследуемого языка, который, обладая хорошим языковым чутьем, пользуется кроме того лексико-статистическим справочным материалом.

Согласно полной программе первой схемы испытуемый должен после-довательно угадывать достаточно большое количество текстов (обычно око-ло ста) каждый длиной в 100-200 букв. Угадывание по каждой буквенной по-зиции осуществляется вплоть до получения правильного результата. В про-токоле полной программы фиксируется число попыток, понадобившихся ис-пытуемому для того, чтобы определить букву, которая стоит на n-ом шаге те-кста. Особо выделяются достоверные продолжения. Ими считаются буквы и пробелы (#), появление которых на n-ом шаге текста предопределено пред-шествующей n–1 буквенной цепочкой (ср. буквы о, # в с/ф которого#). Ре-зультаты угадывания после их корекции с помощью толковых и орфогра-фических словарей обобщаются в виде матрицы. На пересечении ее столбцов и строк стоят числа, указывающие на то количество попыток, которое пона-добилось испытуемому, чтобы получить правильную информацию о букве. При проведении полной программы, учитывающей вероятности достоверных продолжений qⁿ₀ и вероятности qⁿ_k угадать букву с k-той попытки, истинное значение информации, которое несет лингвистическая единица, стоящая на n-м шаге текста, оценивается двойным неравенством:

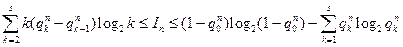. (5.5)

Здесь левая часть неравенства представляет собой нижнюю (H_n = I_n), а правая часть указывает на верхнюю ( 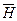_n = _n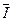) границы интервала, в котором заклю-чено истинное значение информации I_n.

При использовании сокращенной программы угадчик называет наибо-лее вероятную для данной позиции букву. Экспериментатор в ответ либо со-общает, что буква отгадана правильно, либо, если она указана неверно, назы-вает правильную букву. В протоколе сокращенного эксперимента для каждой n-ой позиции i-того текста отмечается один из трех результатов: достоверное продолжение (0), угадывание с первой попытки (1), неверное угадывание (2). Реализация сокращенной программы даёт верхнюю, завышенную оценку эн-тропии/информации. Она имеет вид:

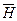_n’ = 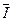_n’ = H₃ (1 – qⁿ₀ – qⁿ₁) + (1 – qⁿ₀) log₂ (1 – qⁿ₀) – qⁿ₁ log₂ qⁿ₁ – (1 – qⁿ₀ – qⁿ₁) log₂ (1 – qⁿ₀ – qⁿ₁), (5.6)

Здесь H₃ – та неопределенность, которую несет третья буква текста при условии, что известны две предшествующие букв (cм. выражение 5.4).

Применение традиционных оценок достоверности выше описанных ин-формационных измерений наталкивается на два препятствия: нестационар-ность энтропийного строения текста и применение логарифмической меры. Поэтому приходится прибегать к таким приемам, как сравнение информаци-онных оценок, получаемых с помощью разных приемов угдывания (табл.14). Кроме того, эти результаты сопоставляют с информациионными оценками, полученными из расчета вероятностных спектров с/ф, букв, слогов, или пу-тем исследования дальних корреляциионных связей в тексте. Пытаются так-же применить нормированный критерий c² и критерий знаков.

5.1.3.Контекстная связанность текста

Наблюдение за ходом как коллективного, так и индивидуального угадывания показывает, что наибольшая неопределенность в предсказании буквы или другой ЛЕ наблюдается в самом начале текста. Затем, по мере движения по тексту вправо она последовательно убывает так, что

(H₁= I₁)>( H₂= I₂)> … ( H_n = I_n ) > … >( H_¥.= I_¥.). (5.7)

Последний член неравенства (5.7) оценивает ту информацию, которую извл-екает угадчик при отгадывании участка буквы, сколь угодно далеко отстоя-щей от начала текста. Величину I_¥ мы будем называть п р е д е л ь н о й

с и н-т а к т и ч е с к о й и н ф о р м а ц и е й связного текста. Предельная

Таблица 14. Энтропия (в дв. единицах) и избыточность (в %)

текстов в языках разной типологии и происхождения [109]

Язык и его раз-новидности	Индивидуальное угадывание	Коллективное угадывние
_ Н	H	R	_ R	H	R
Английский: - разгов. речь; - беллетристика; - публицистика и научно-техничес-кая речь; - переговоры земля-воздух; - язык в целом: 1) носители; 2)русские студенты: I курс; II курс; III курс; IV курс	1,47 1,10     0,82   1,35	0,90 0,65     0,37   0,74	69,4 77,1     82,9   71,9	81,2 86,5     92,1   84,5	0,24   *1,75     1,59 1,31 1,22 1,30	95,0     66,6 72,5 74,4 72,7
Немецкий: - разгов.речь; - беллетристика; - научные и газет- ные тексты; - язык в целом	1,24 1,36   0,97 1,36	0,74 0,83   0,56 ..0,71	73,9 71,4   79,6 71,4	84,4 82,5   88,2 85,1
Испанский: - язык в целом: 1) носители: 2) русские студенты: I курс II курс III курс IV курс					1,05     1,81 1,32 1,15 0,97	77,8     61,7 72,1 75,7 79,5
Румынский: - разгов. речь - беллетристика - публицистика и научно-техн. речь - язык в целом	1,24 1,26   1,23 1,34	0,71 0,78   0,68 0,72	74,2 73,8   74,4 72,1	85,4 83,8   85,7 85,0
Французский: - разгов.речь; - беллетристика; - научные и газет-ные тексты; - язык в целом 1) носители:   2)русские студенты: I курс; II курс; III курс; IV курс; V курс	1,32 1,36   0,77   1,38	0,81 0,78   0,45   0,79	72,0 71,0   83,9   70,6	82,8 83,6   90,4   83,4	**1,11   **0,61   1,05 **1,00     1,74 1,39 1,35 1,32 1,28	**76,3   **87,0   77,7 **78,7     63,0 70,5 71,3 72,0 72,8
Русский: - разгов. речь; - беллетристика; - публицистика и научно-технич. речь; - переговоры земля-воздух; - язык в целом; - патологическая речь (шизофрени- ки)	1,40 1,19     0,83     1,37     1,52	0,83 0,70     0,49     0,82	72,0 76,3     83,4     72,1     69,6	83,4 86,0     90,1     83,6	0,25 *1,10	95,0 *78,0
Польский: - разгов. речь; - беллетристика; - публицистика и научно-техниче-ская речь; - язык в целом	1,18 1,29     0,83 1,28	0,69 0,83     0,53 0,76	76,3 74,5     83,6 74,7	86,3 83,6     89,5 85,0
Чешский: - беллетристика	1,38	0,78	73,9	85,3
Болгарский: - язык в целом					0,91	81,6
Армянский: - беллетристика	1,38	0,78	73,9	85,3
Азербайджан-ский: - язык в целом	1,17	1,07	65,2	79,0
Казахский: - разгов. речь; - беллетристика; - публицистика и научно-техн. речь; - язык в целом	1,56 1,35   1,18 1,51	0,79 0,61   0,65 0,82	70,0 74,3   77,3 70,9	84,8 88,3   87,5 84,2
Узбекский: - язык в целом	1,48	0,79	72,0	85,0
Эстонский: - разгов. речь; - беллетристика; - публицистика и научно-технич. речь; - язык в целом					1,52 1,15     1,18 1,27	67,3 75,9     * 74,6 72,6
Адыгейский: - беллетристика	2,26	1,52	56,0	68,2

Примечание к табл. 14: Основная часть энтропийно-информационных оценок, приведенных в таблице получено путём угадывания информантами текста и его обработки по программам Шеннона-Пиотровского. Для провер-ки достоверности этих данных привлечены энтропийно-информационные оценки, полученные разными авторами с помощью иных методик. Одной звёздочкой (*) помечена оценка, полученная американскими авторами отно-сительно английского текста [86. C. 11]. Двумя звездочками (**) отмечены оценки энтропии, полученные Н.В.Петровой [107a] по методу Колмогорова для русского и французского языков.

информация в идеальной схеме текста всегда будет больше нуля. Это и понятно. Всякий текст, будучи образован из сложных знаков (слов, c/c, предложений), обладающих практически неограниченной комбинаторной способностью, имеет несколько продолжений или, иначе говоря, всегда обладает неопределенностью выбора. Даже в тех случаях, когда данный шаг конкретного текста предусматривает единственно возможное продолжение, всегда найдутся последующие шаги, которые дадут несколько возможных продолжений. Величину I_¥ можно рассматривать как суммарную оценку информации, получае-мой идеальным адресатом-угадчиком для данного языка или его разновидности от одной буквы на n-й позиции текста, на которую действуют комбинаторно-статистические, семантико-синтакси-ческие и прагматические ограничения предшествующего фрагмента (n – 1 букв). Их оценивают с помощью к о н т е к с т н о й с в я з а н н о с т и текста

K_n = I₀ – I_nbits, (5.7а)

которая при неограниченном движении по тексту стремится к п р е д е л ь н-о й контектной связанностью текста K_¥ = I₀ – I_¥ bits. Абсолютные величины I_n ,K_n ,I_¥ и K_¥ нельзя сравнивать по разным языкам, поскольку они зависят от числа букв в каждом национальном ал-фавите. Поэтому при сравнении информационных свойств разных языков удобнее пользоваться величиной избыточности (R), в которой названные величины соотнесены с энтропией алфавита и, таким образом, не зависят от его длины. При этом имеем:

R = (H₀ – H_¥) / H₀) 100% или R = (K_¥ / H₀) 100%. (5.8)

Оценки величин H_¥.= I_¥ и R по языкам см. в табл. 14.

Анализ полученных данных показывает, что языки разной типологии и происхождения имеют примерно одинаковый уровень избыточности. Расхождения в значениях R, обнаруживаются:

– при сопоставлении разновидностей и стилей языка,

– при сопоставлении результатов угадывания текстов родного и иностранного языков,

– при сравнении текста, порожденного нормальным человеком, и речи душевно больных людей.

Отсюда следует, что, во-первых, основные глубинные информацион-ные характеристики текста не зависят от строя и происхождения языка, но определяются физиологическими и коммуникативно-семиотическими свой-ствами нашего сознания, во-вторых, колебания этих характеристик зависят от ситуации общения, состояния РМД и от степени владения коммуникан-тами данным языком.

Поскольку значения R не зависят от длины и от характера алфавита, то избыточность может выступать как мера синергетической организации тек-ста. Это позволяет использовать величины R, а отчасти K и H=I в качестве диагностических показателей состояния психики, а также оценки уровня лингвистической компетенции и богатства тезауруса коммуникантов.