Логическое программирование

Приведенный метод резолюций служит основой языков логического программирования. Главное отличие языков логического программирования от процедурных языков заключается в том, что программа не указывает как что-то сделать, а описывает некоторые элементы и связи между ними (модель) и ставит цель, т. е. задает вопрос об этой системе. На формальном языке это означает проверить истинность предложения на данной системе. При этом компьютер самостоятельно выбирает стратегию для решения поставленных вопросов.

Логическая программа представляет собой конечный набор выражений следующих видов:

факты: 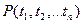, (1)

правила: 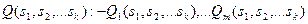, (2)

где 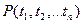, 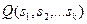- атомарные формулы.

Правило читается как: «если истинны 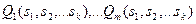, то истинно 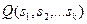». Формула 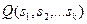называется заголовком правила.

Правила позволяют выводить новые факты из уже существующих. Факты определяют отношения между объектами.

Для выполнения программы необходимо обратиться к целевому запросу (цели), которая представляет собой последовательность атомарных формул вида:

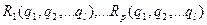. (3)

Выполнение программы состоит в попытке решить задачу, т .е. доказать целевое утверждение, используя факты и правила.

Каждому факту (1) поставим в соответствие предложение:

А: 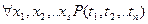, где 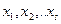- все переменные, входящие в формулу .

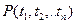Каждому правилу (2) поставим в соответствие предложение:

В: 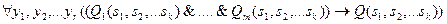, где 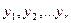- все переменные, входящие в формулы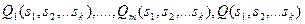

Запросу (3) поставим в соответствие формулу:

С: ,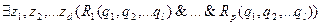

где кванторы связывают все переменные.

Нужно доказать

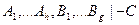
Для доказательства используется метод резолюций.

Тема 5. Теория алгоритмов

Интуитивное понятие алгоритма

Для решения ряда однотипных задач можно использовать чисто механические вычислительные процессы. С их помощью искомые величины вычисляются последовательно из данных величин по определенным правилам. Описание таких процессов принято называть алгоритмами.

Алгоритм – это строгое предписание, определяющее вычислительный процесс как последовательность шагов, которая приводит от изменяемых начальных данных к конечному результату. Это фундаментальное и неопределяемое понятие.

Свойства алгоритмов

2. Массовость: алгоритм должен решать не одну конкретную задачу, а целый класс подобных задач.

3. Элементарность шагов: алгоритм разбивается на этапы, каждый из которых должен быть простым и локальным.

4. Детерминированность: после выполнения очередного этапа однозначно определено, что делать дальше.

5. Результативность: алгоритм должен приводить к решению задачи за конечное число шагов.

Примеры алгоритмов:

1. Нахождение наибольшего общего делителя.

2. Вычисление ранга целочисленной матрицы.

3. Построение ДНФ и КНФ в логике высказываний.

Интуитивное понятие алгоритма позволяет определить является ли данный процесс алгоритмом. Но существуют и алгоритмически неразрешимые задачи, т .е. задачи для которых построить алгоритм в принципе невозможно.

Теория алгоритмов занимается проблемой алгоритмической разрешимости, т. е. определением того, возможно ли вообще построить алгоритм для задач данного типа.

Но для того, чтобы доказать, что алгоритм не существует, надо точно знать, что такое алгоритм.

Начиная с 30-х годов XX века, было предложено несколько уточнений понятия алгоритма. К ним относятся:

· Рекурсивные функции.

· Машина Тьюринга.

· Нормальные алгорифмы Маркова.