Закон исключенного третьего 1 страница

.

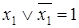Пример.

Для доказательства закона исключенного третьего используем таблицу истинности (табл. 6.11).

Таблица 6.11 - Закон исключенного третьего

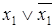Столбец истинности, представляющий левую часть доказываемого тождества, равен константе единицы, что и требовалось доказать.

Закон противоречия

.

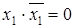Пример.

Для доказательства закона противоречия используем таблицу истинности (табл. 6.12).

Таблица 6.12 - Закон противоречия

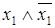Данный закон является двойственным к доказанному выше закону исключенного третьего.

Закон тождества (свойство констант)

; ;

; .

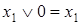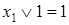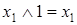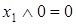Пример.Для доказательства закона тождества (свойство констант) используем таблицу истинности (табл. 6.13).

Таблица 6.13 - Таблицы истинности тождеств

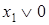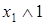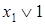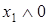Закон поглощения (элиминации)

;

.

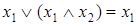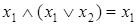Пример.

Докажем закон поглощения (элиминации) аналитически, используя тождества с константами и дистрибутивный закон:

;

.

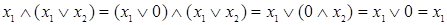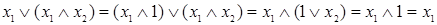Закон инволюции (двойного отрицания)

.

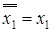Пример.

Для доказательства закона инволюции (двойного отрицания)используем таблицу истинности (табл. 6.14).

Таблица 6.14 - Закон двойного отрицания

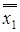Законы де Моргана

;

.

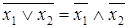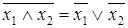Пример.

Для доказательства закона де Морганаиспользуем таблицу истинности (табл. 6.15).

Таблица 6.15 - Доказательство закона де Моргана

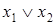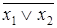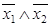Второй закон де Моргана является двойственным первому и, значит, также является верным.

6.8 Контрольные вопросы и задания

1. Какие переменные называются булевыми или логическими переменными?

2. Какая функция называется логической (булевой, переключательной)?

3. Приведите примеры задания (использования) булевых переменных в языках программирования.

4. Как называется совокупность конкретных значений аргументов булевой функции?

5. Сколько элементов-слов содержит -мерный булевый куб?

6. Что представляет собой область определения и область значений булевой функции?

7. Какая булева функция называется полностью определенной?

8. Как определить число всех булевых функций, зависящих от переменных.

9. Перечислите способы задания булевых функций.

10. Что представляет собой таблица истинности (соответствия) булевой функции. Назовите правила её построения.

11. Перечислите булевы функции от одной переменной.

12. Приведите примеры элементарных функций двух переменных.

13. Перечислите основные булевы функции от двух переменных.

14. Каким образом определяется номер булевой функции? Номер интерпретации?

15. Дайте определение формулы для задания булевой функции. Что такое суперпозиция булевых функций?

16. Какие знаки используются при образовании (построении) формул? Какой приоритет определен для операций алгебры логики?

17. Какая запись формул называется инфиксной? Приведите примеры.

18. Чем отличается табличный и формульный способ задания булевых функций? В каких случаях применяется каждый из них?

19. Какие формулы называются равносильными или эквивалентными?

20. Перечислите основные методы определения равносильности формул.

21. Дайте определение двойственной функции.

22. Дайте определение самодвойственной функции.

23. Каким образом формируется таблица истинности двойственной функции?

24. Сформулируйте принцип двойственности булевых функций.

25. Дайте определения двухэлементной булевой алгебры и алгебры логики.

26. Перечислите основные законы булевой алгебры.

27. Каким способом можно доказать законы булевой алгебры.

28. Сформулируйте и запишите тождества для законов булевой алгебры.

Лекция 7. Нормальные формы булевых функций

7.1 Нормальные формы булевых функций, основные понятия

При практическом применении теории булевых функций часто ставится задача поиска наиболее простой (в определенном смысле) формулы среди всех эквивалентных между собой формул, представляющих рассматриваемую булеву функцию.

На примере булевых функций обсудим важное понятие «нормальной формы», то есть синтаксически однозначного способа записи формулы, реализующей заданную функцию. Данный способ основан на рассмотрении представления логических функций в виде суперпозиций функций 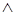(«и»), 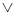(«или»), («не»).

Введем понятия, определяющие способ представления формул в виде дизъюнктивных и конъюнктивных нормальных форм.

Определение.

Элементарной конъюнкцией называется конъюнкция любого числа булевых переменных, взятых с отрицанием или без него, в которой каждая переменная встречается не более одного раза. Элементарной конъюнкцией, содержащей ноль переменных, будем считать константу 1.

Пример.

Элементарными конъюнкциями для функции от одной переменной могут быть , 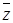; для функции от двух переменных - 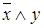, 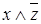; для функции от трех переменных - 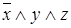, , 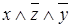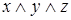и т.д.

Определение.

Дизъюнктивной нормальной формой (ДНФ) называется формула, представленная в виде дизъюнкции элементарных конъюнкций.

Пример.

Если булева функция задана формулой в виде дизъюнкции элементарных конъюнкций, то функция представлена своей дизъюнктивной нормальной формой. ДНФ функции 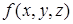может иметь вид .

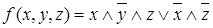Определение.

Члены дизъюнктивной нормальной формы, представляющие собой элементарные конъюнкции букв, называются минтермами -го ранга.

Пример.

Элементарная конъюнкция 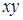является минтермом второго ранга; 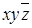- минтермом третьего ранга; 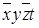- минтермом четвертого ранга и т.п.

Определение.

Конституентой единицы (минтермом -го ранга) называют булеву функцию аргументов, которая принимает значение, равное 1, только на одной интерпретации (наборе).

Пример.Конституента единицы обращается в единицу только при одном соответствующем ей наборе значений переменных, который получается, если все переменные принять равными единице, а их отрицания - нулю, например, конституенте единицы 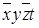соответствует набор (0101), а конституенте единицы 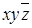- набор (110).

7.2 Совершенные нормальные формы булевых функций

Среди множества эквивалентных формул, представляющих выбранную булеву функцию , выделяется одна формула, которая называется совершенной нормальной формой функции . Она имеет регламентированную логическую структуру и однозначно определяется по функции.

Определение.

Совершенной дизъюнктивной нормальной формой (СДНФ) функции 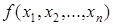, содержащей различных переменных, называется дизъюнктивная нормальная форма, обладающая следующими свойствами:

а) в ней нет одинаковых слагаемых;

б) ни одно слагаемое не содержит двух одинаковых множителей;

в) никакое слагаемое не содержит переменной вместе с её отрицанием;

г) в каждом слагаемом содержится в качестве множителя либо переменная 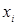, либо её отрицание, где .

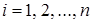Условия а), б), в), г) являются необходимыми и достаточными для того, чтобы ДНФ была СДНФ.

Определение.

Совершенной дизъюнктивной нормальной формой (СДНФ) булевой функции называется формула, представленная в виде дизъюнкции конституент единицы данной функции.

В каждом члене СДНФ представлены все переменные (либо в прямом, либо в инверсном виде).

Всякая булева функция 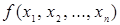, которая не является тождественным нулем, имеет:

- несколько ДНФ;

- одну и только одну СДНФ (количество её членов равно количеству единичных значений функции).

Определение.

Элементарной дизъюнкциейназывается дизъюнкция любого числа булевых переменных, взятых с отрицанием или без него, в которой каждая переменная встречается не более одного раза. Элементарной дизъюнкцией, содержащей ноль переменных, будем считать константу 0.

Пример.

Элементарными дизъюнкциями для функции от одной переменной могут быть , 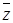; для функции от двух переменных - 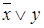, 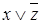; для функции от трех переменных - 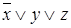, , 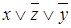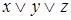и т.д.

Определение.

Конъюнктивной нормальной формой (КНФ) называется формула, представленная в виде конъюнкции элементарных дизъюнкций.

Пример.

Конъюнктивная нормальная форма функции 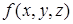может иметь вид .

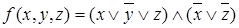Определение.

Члены конъюнктивной нормальной формы, представляющие собой элементарные конъюнкции букв, называются макстермами -го ранга.

Пример.Элементарная дизъюнкция 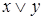является макстермом второго ранга; 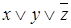- макстермом третьего ранга; 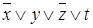- макстермом четвертого ранга.

Определение.

Конституентой нуля (макстермом -го ранга) называют булеву функцию аргументов, которая принимает значение, равное 0, только на одной интерпретации (наборе).

Пример.

Конституента нуля обращается в ноль только при одном соответствующем ей наборе значений переменных, который получается, если все переменные принять равными нулю, а их отрицания - единице, например, конституенте нуля 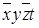соответствует набор (1010), конституенте нуля 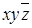- набор (001), конституенте нуля 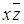- набор (01).

Пример.

Представим в табл. 7.1 конституенты единицы и нуля, соответствующие интерпретациям функций трех переменных. Для каждой интерпретации функции имеются единственные соответствующие ей конституента единицы и конституента нуля.

Таблица 7.1 - Конституенты единицы и нуля функций трех переменных

Номер интерпретации	Интерпретация	Конституента единицы	Конституента нуля

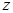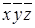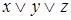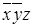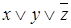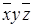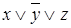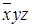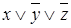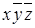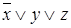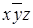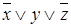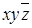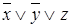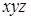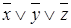Различных конституент единицы и нуля для функции переменных 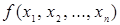имеется столько же, сколько и интерпретаций этой функции, т.е. .

Определение.

Совершенной конъюнктивной нормальной формой (СКНФ) функции 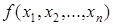, содержащей различных переменных, называется конъюнктивная нормальная форма, обладающая следующими свойствами:

а) в ней нет двух одинаковых множителей;

б) ни один множитель не содержит двух одинаковых слагаемых;

в) ни один множитель не содержит какой-нибудь переменной вместе с её отрицанием;

г) каждый множитель содержит в качестве слагаемого либо переменную 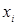, либо её отрицание 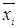для любого .

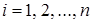Условия а), б), в), г) являются необходимыми и достаточными для того, чтобы ДНФ была СДНФ.

Определение.

Совершенной конъюнктивной нормальной формой (СКНФ) булевой функции называется формула, представленная в виде конъюнкции конституент нуля данной функции.

В каждом члене СКНФ представлены все переменные (либо в прямом, либо в инверсном виде).

Всякая булева функция 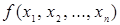, которая не является тождественной единицей, имеет:

- несколько КНФ;

- одну и только одну СКНФ (количество её членов равно количеству единичных значений функции).

Различные нормальные формы (дизъюнктивные и конъюнктивные) можно получить, используя следующие основные подходы, в зависимости от того, каким способом представлена анализируемая булева функция:

- разложить булеву функцию по переменным;

- перейти от табличного представления функции к алгебраическому;

- преобразовать произвольную формулу алгебры логики в нормальную форму, проводя тождественные (эквивалентные) преобразования (используя законы (тождества) алгебры логики).

7.3 Теоремы о разложениях булевой функции по переменным

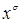Рассмотрим теоремы о разложениях булевой функции по переменным. Для упрощения математических выкладок введем двоичный параметр и обозначение следующим образом: ;

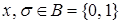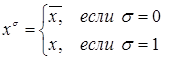и .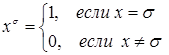

Бинарная функция 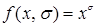представляется формулой .

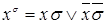Теорема о дизъюнктивном разложении булевой функции 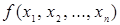по переменным.

Любую булеву функцию 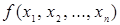можно представить в следующей форме .

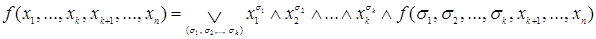Запись 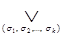означает многократную дизъюнкцию, которая берется по всем возможным наборам значений 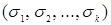при любом .

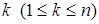Следствие 1. Дизъюнктивное разложение булевой функции 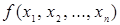по одной переменной.

Любую булеву функцию 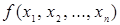можно представить в следующей форме .

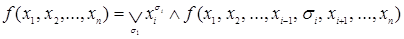Запись 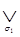означает, что дизъюнкция берется по всем значениям 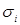, то есть по 0 и по 1. Запись 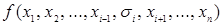обозначает значение функции на наборе 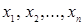, где вместо значения переменной 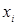подставлено .

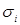Следствие 2. Дизъюнктивное разложение булевой функции 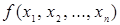по всем переменным.

Любую булеву функцию 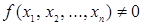можно представить в следующей форме: .

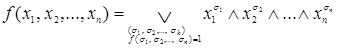Запись 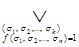означает, что дизъюнкция берется по всем наборам значений 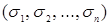, на которых .

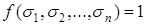Пример.

Запишем дизъюнктивное разложение функции 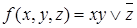по всем переменным.

Определим значение функции на каждой интерпретации: , ,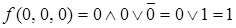

, ,

, ,

, .

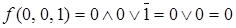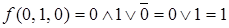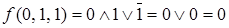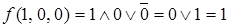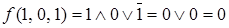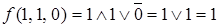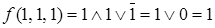Запишем формулу, используя следствие 2 теоремы о разложении функций:

.

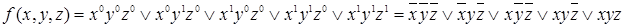СДНФ функции является результатом дизъюнктивного разложения функции по всем переменным. СДНФ функции содержит только 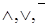, следовательно, применив к СДКФ принцип двойственности, можно получить двойственное представление, которое называется конъюнктивным разложением.