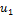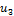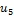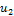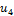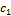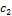Принцип включения и исключения.

Правила образования формул

a) все простые высказывания – суть формулы.

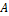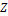b) если и – формулы, то 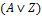– формула.

c) еслиA – формула, то 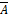– формула.

Аксиомы вывода( )).

A1: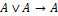

A2: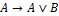

A3: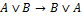

A4: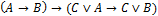

Правила вывода

· Правило подстановки ( 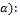если A – выводимая формула в исчислении высказываний, и всюду в этой формуле вместо некоторой переменной в A произвести подстановку другой выводимой формулы, то новая формула тоже выводима.

· Правило заключения: (Modusponens 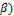: 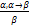(если 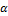и формула 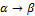выводимы, то 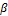- выводима).

8. Суперпозиция булевых функций. Функционально полные системы функций. Критерий полноты. Базис.

Функции, которые определены на логических переменных и принимают значения 0 или 1 называются логическими или булевыми: .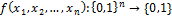

Пусть дана системабулевых функций с произвольным числом аргументов 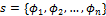. Функция 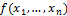являетсясуперпозицией системы , если:

1. 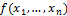получили из 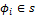путем переименования переменных;

2. 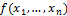получили из 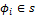путем постановки вместо некоторых переменных функций из ;

3. 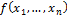получена конечным числом применения пунктов 1 и 2.

Система функций называется замкнутой, если любая подстановка из функций данной системы дает новую функцию,которая также принадлежит этой системе.

Система логических функций F называется полной, если все остальные логические функции могут бытьпредставлены с помощью формул через суперпозицию функции этой системы F.

Классы функций замкнутые относительно подстановки:

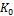· – класс функций,сохраняющий константу 0: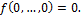

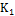· – класс функций, сохраняющих константу 1: .

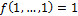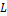· – класс линейных функций (функций представимых полиномом Жегалкина первой степени:

)

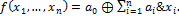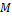· – класс монотонных функци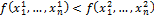й: при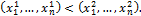

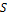· – класс самодвойственных функций: .

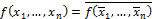Критерий Поста-Яблонского. Система полна тогда и только тогда, когда она по совокупности не принадлежит ни одному из замкнутых классов .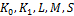

Базисомили базисным набором логических функций называется такая полная система функций, что удаление из нее хотя бы одной логической функции нарушает свойство полноты.

Логические базисы:

· аддитивный: ;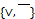

· конъюнктивный: ;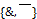

· импликативный: ;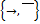

· импликативный: ;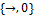

· Жегалкина: ;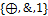

· Шеффера: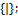

· Веба: .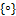

9. Размещения, размещения без повторения, перестановки, сочетания. Их комбинаторные характеристики. Формула включений и исключений.

Размещением из n элементов по k называется расположение предметов (объектов) на 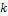местахпри условии, что каждое место занято в точности одним предметом и все предметы различны.

Размещение с повторениями - это размещение предметов в предположении, что каждый предмет может участвовать в размещении несколько раз.

Виды размещений
Перестановки (порядок мест важен)	Сочетания (порядок мест не важен)
без повторений	с повторениями	без повторений	с повторениями

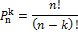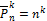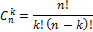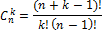Правило суммы

Если дано разбиение множеств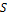а вида 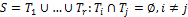и, если 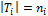, то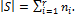

Правило произведения

Пусть 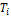–множество, с 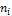элементами, то 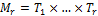– множество, с 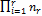элементами.

Принцип включения и исключения.

Пусть дано 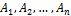– конечные множества, которые могут пересекаться, тогда формула включений и исключений утверждает:

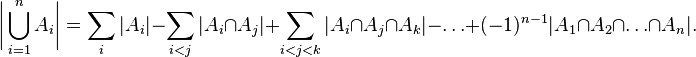
В частности:

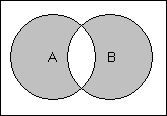
· для двух множеств .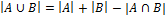

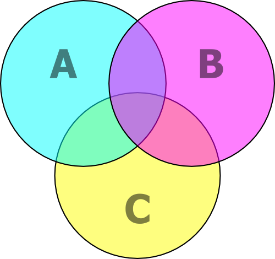
· для трех множеств .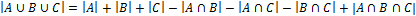

10. Операции над графами.

Граф – это пара 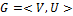, где:

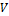· – носитель графа (конечное множество вершин);

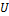· – сигнатура графа (множество ребер для графа или дуг для орграфа).

Если порядок элементов в паре 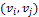имеет значение, то это орграф, рёбра орграфа называются дугами.

Две вершины называются смежными, если они являются концевыми для некоторого ребра. Два ребра называются смежными, если они имеют одну общую концевую вершину. Ребро и вершина называются инцидентными, если эта вершина является концевой для этого ребра.

Операции над графами.

1. Удаление ребра:

.

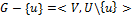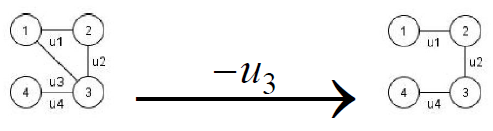
2. Удаление вершины:

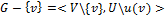, где 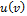– множество ребер, инцидентных с v.

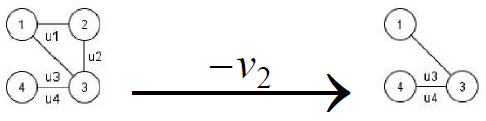
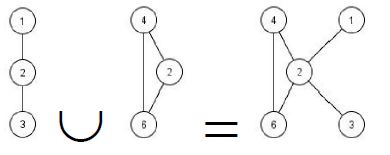
3. Объединение:

.

4. Сложение:

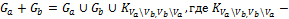двудольный граф, построенный на необщих вершинах обоих графов..

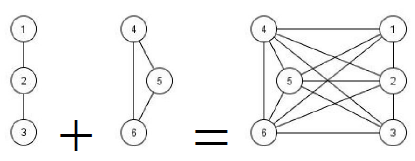
5. Дополнение:

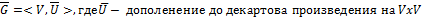за исключением рефлексивных дуг.

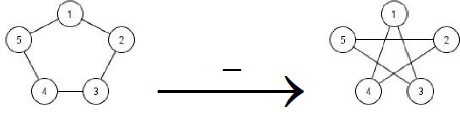
6. Декартово произведение:

.

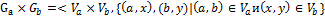11. Компонента сильной связности орграфа. Алгоритм порождения компонент сильной связности. Конденсат графа.

Вершины 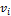и 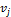сильно связны, если существуют пут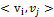и и 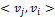.Граф сильно связный, если любые две его вершины сильно связны.

Максимальный по включению вершин подграф орграфа, любые две вершины которого сильно связны, называется компонентой сильной связности орграфа (КСС).

Свойства КСС:

· Разбиение графа на КСС – разбиение на классы эквивалентности.

· Каждая вершина принадлежит ровно одной компоненте сильной связности орграфа.

· Вершины. которые образуют цикл, входят в одну КСС.

Вычисление КСС.

Введем обозначения:

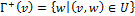· – множество вершин, положительно-смежных с .

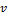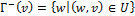· – множество вершин, отрицательно-смежных с .

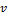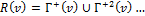· –множество достижимых вершин.

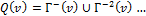· – множество ко-достижимых вершин.

· .

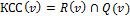Алгоритм нахождения КСС:

1. Поместить свободную вершину с минимальным номером в ( 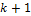)-ю КСС.

2. Вычислить достижимые и ко-достижимые вершиныиз .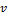

3. Получить КСС пересечением этих множеств. Переход к пункту 1.

Конденсатоморграфа 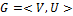называется граф 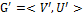,полученный в результате стягивания вершин каждой компоненты в одну.

Пример.

;

.

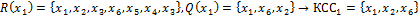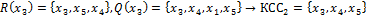Конденсат:

12. Цикломатика графов. Цикломатическое число. Цикломатический базис. Связь циклов графа с цикломатическим базисом.

Циклом называют путь, в котором первая и последняя вершины совпадают.

Цикл называется:

· простым, если ребра в нём не повторяются;

· эйлеровым,если онпроходит через все ребра этого графа ровно один раз;

· гамильтоновым, если он проходит через все вершины графа ровно один раз;

· составным, если в нем повторяется хотя бы одно ребро;

· сложным, если в нем повторяется хотя бы одна вершина.

Каждый цикл может быть представлен в качестве двоичного вектора 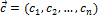, где

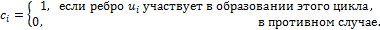
Пространство циклов – пространство векторов 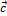.Цикломатическая матрица­– матрица, каждая строка которой вектор .

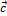Цикломатический базис – совокупность линейно независимых цикловиз пространства циклов, с помощью которых могут бытьполучены все остальные циклы. Мощность базисной системы циклов –цикломатическое числографа 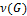.Любые другие циклы могут быть получены как линейная комбинация базисных, причем общее число циклов равняется .

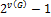Остовное дерево (остов) — это подграф данного графа, содержащий все его вершины, но не содержащим ни одного цикла. Рёбра графа, не входящие в остов, называются хордами графа относительно остова.

Алгоритм нахождения цикломатического базиса:

1. Для графа найти его остовное дерево.

2. Циклы, получаемые в результате поочередного добавления хорд, составляют цикломатический базис.

Пример.

Дан граф.

Его остов.

Таблица циклов   Остов Хорды

Теорема Эйлера. 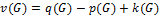, где:

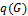· – число ребер графа;

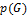· – число вершин графа;

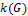· – число компонент связанности графа.

13. Реберные графы. Критерий реберности графа. Алгоритм порождения образа реберного графа.

Пусть 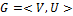– некоторый граф. Назовем граф 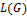реберным графом G, если носитель графа 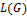совпадает с множеством ребер графа 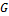, и две вершины в 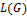смежны, если соответствующие ребра смежны в .

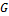Пример.

Образ графа – граф, для которого данный граф является реберным.Граф 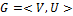обладает свойством реберности, если найдется такой граф 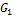, что реберный для него будет изоморфен G.