B) & V &y V x&y
f(x,y)= x  y логикалық функциясының мүлтіксіз дизъюнктивті қалыпты формасы н (МДҚФ) көрсетіңіз:
y логикалық функциясының мүлтіксіз дизъюнктивті қалыпты формасы н (МДҚФ) көрсетіңіз:
B) 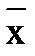 &y V x&
&y V x& 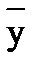
f(x, y) = 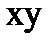

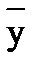 функциясы үшін Жегалкина полиномы төмендегідей:
функциясы үшін Жегалкина полиномы төмендегідей:
D) 1 y xy
f(x,y)=x V y логикалық функциясының мүлтіксіз дизъюнктивті қалыпты формасы н (МДҚФ) көрсетіңіз:
A) &y V x& V x&y
f(x, y) = x V y функциясына құрылған Жегалкина полиномын көрсетіңіз:
B) x y xy
f(x,y,z) = 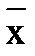
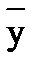 V(x y
V(x y  z) логикалық функциясының мүлтіксіз дизъюнктивті қалыпты формасын (МДҚФ) көрсетіңіз
z) логикалық функциясының мүлтіксіз дизъюнктивті қалыпты формасын (МДҚФ) көрсетіңіз
A) 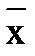 &
& 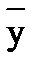 &
& 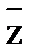 V
V 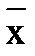 &
& 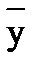 &z V
&z V 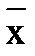 &y&z V x&
&y&z V x& 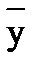 &z V x&y&
&z V x&y& 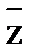
f(x,y,z)=((x®y) (z®y))~(xz®y) функциясының маңызды айнымалылар жиынын көрсетіңіз.
E) {x,y,z}
f(x, y) = x V 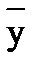 функциясына құрылған Жегалкина полиномы:
функциясына құрылған Жегалкина полиномы:
B) 1 y xy
f(x1, …,xn) және g(x1,…,xn) қандай шарт орындалғанда бір-біріне түйіндес деп аталады.
D) f(x1, …, xn) = 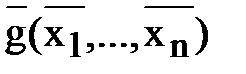
f(x,y)= x ~ y логикалық функциясының мүлтіксіз дизъюнктивті қалыпты формасы н (МДҚФ) көрсетіңіз
A) x &y V 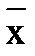 &
& 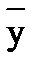
f(x,y)= x | y логикалық функциясының мүлтіксіз дизъюнктивті қалыпты формасы н (МДҚФ) көрсетіңіз
A) 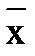 &
& 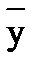 V
V 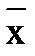 &y V x&
&y V x& 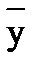
f(x, y) = x V y функциясына Жегалкин полиномы төмендегідей:
B) x y xy
f(x, y) = 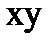 →y функциясына құрылған Жегалкина полиномын көрсетіңіз:
→y функциясына құрылған Жегалкина полиномын көрсетіңіз:
D) 1 y xy
f(1,1, …,1)=1 шарты орындалатын f(x1, …,xn) функциясы қалай аталады?
D)1-ді сақтайтын функция;
ХХХХХХХХХХХХХХХХХ
Х жиынының Р предикатына қатысты образы деп .. жиынын айтады.
D) 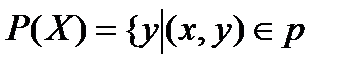 қандай да бір х үшін
қандай да бір х үшін 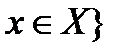 .+
.+
Х жиынының Р предикатына қатысты прообразы деп .. жиынын айтады.
Е) 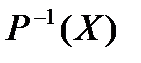
Ш-Ш-Ш-Ш-Ш-Ш-Ш-Ш-Ш
Шкафтағы әртүлі 8 галстуктен 2 галстукті неше әдіспен таңдауға болады?
B) 28
Шетел тілдерін оқитын 37 студенттің 15 –і неміс тілін, 15-і ағылшын тілін,француз тілін 14 студент үйреніпті. Ағылшын және француз тілдерін 4 студент, неміс және француз тілдерін 2-студент, неміс және ағылшын тілдерін 2 студент біледі. Қанша студент барлық тілді үйренген?
E) 1
Шеффер штрихының 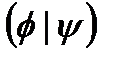 формуласымен анықталуы бойынша
формуласымен анықталуы бойынша 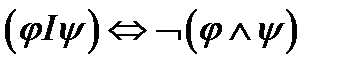 ... деп аталады.
... деп аталады.
А)Антиконъюкция;
ЭЭЭЭЭЭЭЭЭЭЭЭЭЭЭЭЭЭ
эквивалентті формулаларды көрсетіңіз:
1) 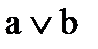 2)
2) 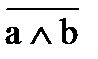 3)
3) 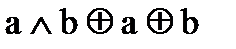
C) 1, 3
эквивалентті формулаларды көрсетіңіз:
1) 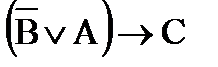 2)
2) 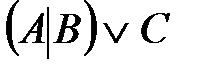 3)
3) 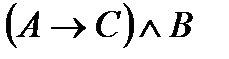
E) ешқайсысы эквивалентті емес
САНДАР
1, 2, 3, 4, 5, цифрларынан қанша төрт орынды сан құруға болады?
C) 625
2, 3, 5, 9 цифрларынан қанша әр түрлі үш орынды сан құруға болады?
D) 64
4 түсті материал бар болса қанша әдіспен үшжолақтан тұратын жалау құруға болады?(жолақтар әр түсті болуы керек)
C) 24
4 элементтен тұратын жиынды қанша әдіспен 3 бос емес бөліктерге бөлуге болады?
D) 4
5 адамнан тұратын топты неше әдіспен бос емес үш жиынға бөлуге болады?
C) 25
5 адамнан тұратын топқа 3 жолдама бөлінген. Жолдамалар әртүрлі болса, оларды қанша әдіспен үлестіруге болады?
B) 60
5 әйел 7 ер адамнан тұратын қазылар алқасы 6 әйел және 10 ер адамнан тұратын тiзiмнен таңдалуы тиiс. Құрамы неше түрлi қазылар алқасын таңдауға болады?
B) 720
5 кітапты сөреге қанша әдіспен қоюға болады?
C) 120
5 элементтен тұратын жиынды қанша әдіспен 3 бос емес бөліктерге бөлуге болады?
B) 25
5 элементтен тұратын жиынды қанша әдіспен 3 бос емес бөліктерге бөлуге болады?
C) 25
6 адамды президумға қанша әдіспен отырғызуға болады?
E) 720
6 түрлі газеттен қанша әдіспен әр түрлі 5-еуін таңдауға болады?
D) 6
7 адамды дөңгелек столдың басына қанша әдіспен отырғызуға болады?
C) 5040
10 студентті 5 студенттен 2 топқа қанша әдіспен бөлуге болады?
C) 126
25 адамнан тұратын топқа математикадан болған бақылау жұмысына алгебра мен геометриядан есептер ұсынылды. Алгебраның есептерін 18 адам , геометрияның есептерін 15 адам, ал алгебраны да геометрияны да 10 адам шығарды. Қанша адам ешқандай есеп шығармады?
E) 2
“36 дан 6” спортлотоға қанша әртүрлі карточка толтыруға болады?
E) 1947792
150 оқушының ішіндегі барлық ер балалар марка жинапты. Оның 52-і Африканың, 34-і Американың,10- ы тек Американың маркаларын жинапты.
Осы оқушылардың ішінен нешеуі қыз бала?
C) 88
