Закон исключенного третьего 11 страница

7. Какую формулу необходимо использовать, чтобы решить задачу о распределении разных предметов с учетом их порядка в урнах?

8. Охарактеризуйте понятие композиции чисел.

9. Дайте характеристику разбиений в комбинаторном анализе.

Лекция 17. Подходы к изучению комбинаторных объектов и чисел

17.1 Понятие продуктивной функции

Пусть задана некоторая последовательность чисел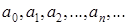

Определение. Если степенной ряд

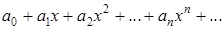(17.1)

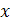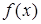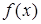совпадает при некоторых с функцией , то называется продуктивной функциейдля последовательности .

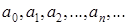С последовательностью 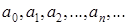можно связать еще один степенной ряд:

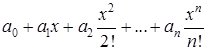(17.2)

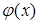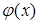Определение. Если этот ряд совпадает с функцией , то называется экспоненциальной продуктивной функцией для последовательности 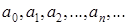Это название объясняется тем, что для последовательности 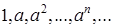экспоненциальной продуктивной функцией (17.2) есть экспонента :

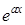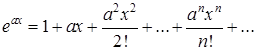(17.3)

Для той же последовательности обычная функция есть :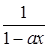

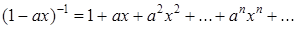(17.4)

Действительно, если 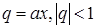, то есть 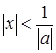, тогда по формуле суммы бесконечно спадающей геометрической прогрессии (17.4) получаем .

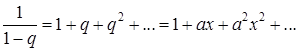В частности, если 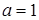, то

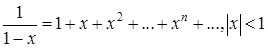(17.5)

Дифференцирование (17.5) приводит к равенству

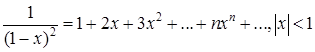(17.6)

Умножение (17.6) на дает

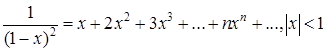(17.7)

Таким образом, 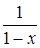есть продуктивная функция для последовательности чисел натурального ряда 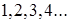(17.6), 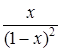– продуктивная функция для последовательности 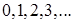(17.7).

Функцию 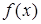, у которой есть производные произвольно высокого порядка при 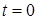, можно считать экспоненциальной продуктивной функцией для последовательности своих производных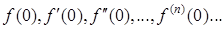

Действительно получается разложение в рад Тейлора:

.

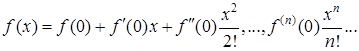17.2 Рекуррентные соотношения в комбинаторике

17.2.1 Задача о наклейке марок

Имеются марки достоинством в 4, 6, 10 копеек. На конверт нужно наклеить марки так, чтобы сумма составляла 18 копеек. Будем считать, что порядок наклеиваемых марок важен, т. е. способы наклейки марок достоинством в 4, 10, 4 копейки и 10, 4, 4 разные способы.

Тогда можно написать следующее рекуррентное соотношение: 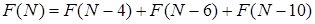, где под 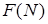понимается количество вариантов наклейки марок общей стоимостью .

Подсчитаем значения 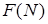для некоторых начальных .

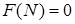при . . . . .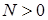

. . . . .

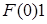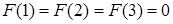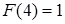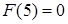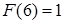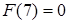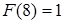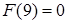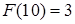Тогда для 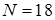получаем:

.

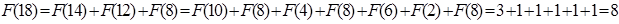17.2.2 Задача об уплате долга

В кошельке имеются монеты достоинством в 1, 2, 3, 5, 10, 15, 20, 50 копеек (по одной штуке). Требуется уплатить долг в 73 копейки.

Запишем рекуррентное соотношение в общем случае, когда монеты имеют достоинства в 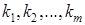копеек и требуется набрать сумму в копеек:

.

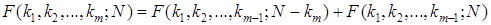Первый член правой части учитывает количество комбинаций, в которых монета старшего достоинства использована, второй член – в которых монета старшего достоинства не использована. Для рассматриваемого примера

(1, 2, 3, 5, 10, 15, 20, 50; 73)= (1,2,3,5,10,15,20;73)+ (1,2,3,5,10,15,20; 23).

Первый член равен 0, так как сумма оставшихся монет меньше набираемой суммы.

Применим ту же рекуррентную формулу к оставшемуся члену. В результате получим:

(1, 2, 3, 5, 10, 15, 20; 23) = (1, 2, 3, 5, 10, 15; 3) + (1, 2, 3, 5, 10, 15; 23)

В первом члене правой части монеты достоинством в 5, 10 и 15 копеек можно не учитывать, так как достоинство каждой из этих монет больше набираемой суммы, т. е. можно правую часть переписать так:

(1, 2, 3; 3) + (1, 2, 3, 5, 10, 15; 23) =

= (1, 2; 0) + (1, 2;3 ) + (1, 2, 3, 5, 10; 8) + (1, 2, 3, 5, 10; 23) =

= 1+ (1; 1) + (1; 3) + (1, 2, 3, 5; 8) + (1, 2, 3, 5, 10; 23).

Очевидно, что (1, 2; 0) = 1; (1, 2; 3) = (1;1) = 1; (1; 3) = 0;

(1, 2, 3, 5, 10; 23) = 0. Поэтому правая часть перепишется в виде:

1 + 1 + 0 + (1, 2, 3, 5; 8) + 0 = 2 + (1, 2, 3; 3) + (1, 2, 3; 8) = 2 + 2 + 0 = 4.

Таким образом, задача имеет 4 различных решения.

Подчеркнем еще раз, что в этой задаче порядок монет не важен.

17.2.3 Задача о размене гривенника (10 копеек)

Рассмотрим задачу, в которой сняты ограничения, как на порядок предметов, так и на их количество: размен гривенника монетами достоинством в 1, 2, 3, 5 копеек.

Для этого случая рекуррентное соотношение имеет вид

(1, 2, 3, 5; 10) = (1, 2, 3; 10) + (1, 2, 3; 5) + (1, 2, 3; 0).

Таким образом, все множество решений разбивается на подмножества в зависимости от числа монет старшего достоинства, использованных для размена.

Находим все 20 способов размена:

5*2; 5+1*5; 3+2*3+1; 2*4+1*2;

5+3+2; 3*3+1; 3+2*2+1*3; 2*3+1*4;

5+3+1*2; 3*2+2*2; 3+2+1*5; 2*2+1*6;

5+2*2+1; 3*2+2+1*2; 3+1*7; 2+1*8;

5+2+1*3; 3*2+1*4; 2*5; 1*10.

17.3 Контрольные вопросы и задания

1. Дайте определение продуктивной функции

2. Дайте определение экспоненциальной продуктивной функции.

3. Приведите примеры задач, которые решаются с использованием рекуррентных соотношений в комбинаторике.

4. Дайте характеристику задачи о наклейке марок.

5. Каким образом может быть решена задача об уплате долга?

6. Дайте характеристику задачи о размене гривенника (10 копеек).

Лекция 18. Происхождение графов. Определение графов

18.1 Разновидности графов. Неориентированный граф. Определения

Определение. Граф или неориентированный граф (рис. 18.1) – это упорядоченная пара 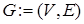, для которой выполнены следующие условия:

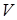- – это непустое множество вершин или узлов,

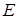- – это множество пар (в случае неориентированного графа – неупорядоченных) вершин, называемых рёбрами.

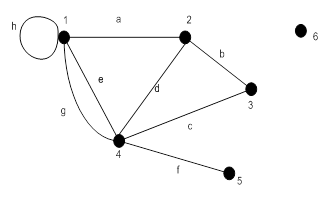
Рисунок 18.1 – Неориентированный граф

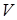(а значит и 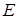, иначе оно было бы мультимножеством) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становится ложным в случае бесконечных множеств.

Определение. Вершины и рёбра графа называются также элементами графа, число вершин в графе 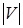– порядком, число рёбер 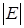– размером графа.

Определение. Вершины и называются концевыми вершинами (или просто концами) ребра 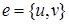. Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними (смежными).

Определение. Два ребра называются смежными, если они имеют общую концевую вершину.

Таким образом, на множествах вершин 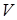и ребер 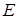неориентированного графа могут быть заданы отношения смежности.

Определение. Вершина называется инцидентной ребру, если она является его концевой вершиной.

Таким образом, на множествах вершин 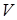и ребер 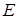графа может быть задано отображение инцидентности.

Определение. Два ребра называются кратными, если множества их концевых вершин совпадают.

Определение. Ребро называется петлёй, если его концы совпадают, то есть .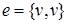

Определение. Степенью 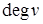(или 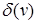) вершины называют количество рёбер, для которых она является концевой (при этом петли считают дважды).

Определение. Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.

Пример.На рисунке 18.1 порядок графа 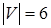(количество вершин), размер графа 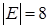(количество ребер); 1 и 2 – смежные вершины (их соединяет ребро 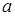); ребра 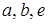– смежные (имеют общую вершину 2); ребра 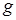и – кратные (соединяют вершины 1 и 4); 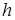– петля; 5 – висячая вершина; 6 – изолированная вершина. Степень вершины 2 – 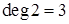, степень вершины 4 – 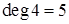, степень вершины 1 – 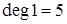(петля считается 2 раза).

18.2 Ориентированный граф. Определения

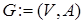Определение. Ориентированный граф (сокращённо орграф) – это упорядоченная пара , для которой выполнены следующие условия:

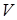- это непустое множество вершин или узлов,

- это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.

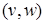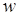Определение. Дуга –это упорядоченная пара вершин , где вершину называют началом, а – концом дуги.

В отличие от неориентированных графов, в ориентированных степень вершины определяется полустепенью захода и полустепенью исхода: соответственно, 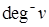и 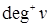(рис. 18.2). Полустепень захода определяется количеством ребер, концом которых является данная вершина, полустепень исхода – количеством ребер, началом которых является вершина.

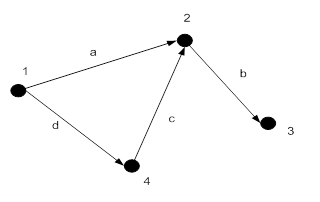
Рисунок 18.2 – Ориентированный граф

Пример.На рис. 18.2 полустепени исхода и захода вершин: ; ; ; .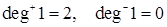

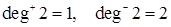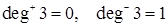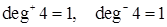18.3 Основные термины для ориентированных и неориентированных графов

Определение. Смешанный граф – это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые – неориентированными (рис. 18.3) Записывается упорядоченной тройкой 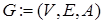, где 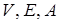определены так же, как выше.

Ориентированный и неориентированный графы являются частными случаями смешанного.

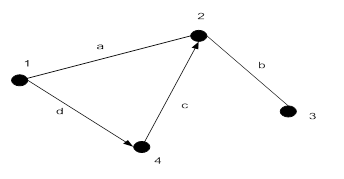
Рисунок 18.3 – Смешанный граф

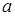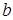На рисунке 18.3 – ребра и – неориентированные, дуг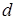и и 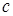– ориентированные.

Определение. Подграфомграфа 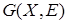называется граф , все вершины и дуги которого содержатся среди вершин и дуг графа , т.е. 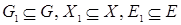. Сам граф является своим подграфом.

Определение. Сам граф по отношению к своим подграфам называется надграфом (или суперграфом).

Определение. Подграф называется собственным, если он отличен от самого графа.

Определение. Для любого подмножества вершин графа порождённым подграфом 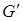называется максимальный подграф графа , множеством вершин которого является .

Определение. Часть графа, которая наряду с некоторым подмножеством ребер (дуг) графа содержит и все вершины исходного графа 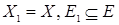называется суграфом.

Определение. Подграф неориентированного графа 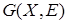называется каркасом, или остовным деревом (остовом) графа 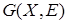, если 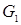– дерево и .

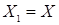Пример.На рис. 18.4 изображен граф и его подграфы. Подграф 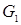– остовный, подграф 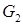– порожденный.

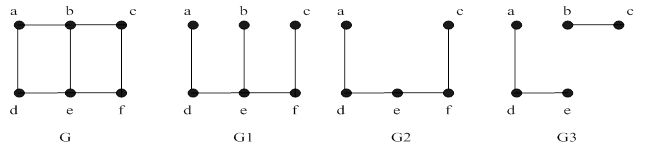
Рисунок 18.4 – Подграфы

Изоморфные графы. Граф называется изоморфным графу 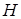(рис. 18.5), если существует биекция f из множества вершин графа в множество вершин графа 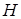, обладающая следующим свойством: если в графе есть ребро из вершины A в вершину B, то в графе 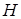должно быть ребро из вершины 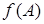в вершину 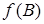и наоборот – если в графе 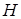есть ребро из вершины A в вершину B, то в графе должно быть ребро из вершины 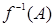в вершину 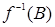. В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.

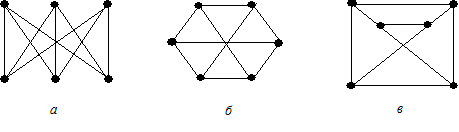
Рисунок 18.5 – Изоморфные графы

Определение. Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.

Определение. Ориентированным путём в орграфе называют конечную последовательность вершин 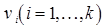, для которой все пары 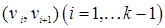являются (ориентированными) рёбрами.

Определение. Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер.

Заметим, что если вершины и являются концами некоторого ребра, то согласно данному определению, последовательность 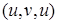является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.

Определение. Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным (или контуром), если он простой, и вершины в нём не повторяются.

Несложно видеть, что:

- всякий путь, соединяющий две вершины, содержит элементарный путь, соединяющий те же две вершины;

- всякий простой неэлементарный путь содержит элементарный цикл;

- всякий простой цикл, проходящий через некоторую вершину (или ребро), содержит элементарный (под-) цикл, проходящий через ту же вершину (или ребро);

- петля – элементарный цикл.

Пример.Рассмотрим граф на рис. 18.6. Он содержит пути: (5, 1, 2), (5, 6, 3, 2), (4, 5, 1, 4, 2) и т.д. Все эти пути простые, элементарным же является только последний. Цикл в графе только один – (1, 4, 5).

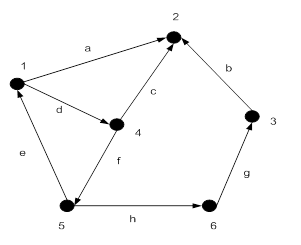
Рисунок 18.6 – Пути на графе

Бинарное отношение на множестве вершин графа, заданное как «существует путь из в », является отношением эквивалентности, и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный.

Определение. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.

Определение. Всякий максимальный связный подграф графа называется связной компонентой (или просто компонентой) графа .