Примеры бинарных отношений. 4 страница
Доказательство теоремы можно провести методом математической индукции.
Следствие теоремы 1.Мощность декартовой степени множества  равна
равна 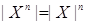 .
.
Пример.Пусть  ,
,  ,
,  .
.
Мощность множества 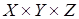 равна
равна 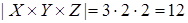 , где
, где 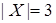 ,
, 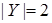 ,
, 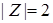 .
.
Мощность множества  равна
равна 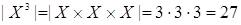 или
или 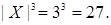
3.2 Понятие отношений. Бинарные и n-арные отношения
Введем формальные понятия отношений.
Говорят, что 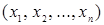 находятся в отношении
находятся в отношении  (
(  является множеством), если
является множеством), если 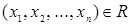 .
.
Определение.  -арное (
-арное (  -местное) отношение
-местное) отношение  на множествах
на множествах 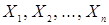 - это подмножество декартова произведения этих
- это подмножество декартова произведения этих  множеств, т.е.
множеств, т.е. 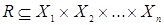 .
.
Определение. Унарное (одноместное) отношение  – это подмножество множества
– это подмножество множества  . Такие отношения называются признаками:
. Такие отношения называются признаками:  обладает признаком
обладает признаком  , если
, если 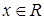 и
и 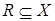 .
.
Свойства унарных (одноместных) отношений – это свойства подмножеств множества  . Поэтому для случая
. Поэтому для случая 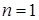 термин «отношение» употребляется редко.
термин «отношение» употребляется редко.
Пример.
Тернарным (трехместным) отношением являются: арифметические операции над числами; отношение между родителями и детьми (отец, мать, ребенок); множество троек нападающих в хоккейной команде.
Пропорция 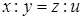 иллюстрирует четырехместное отношение.
иллюстрирует четырехместное отношение.
Наиболее часто встречающимися и хорошо изученными являются бинарные, или двухместные, отношения. Эти отношения возникают между парами объектов.
Определение.
Бинарным отношением на паре множеств  и
и  будем называть подмножество декартового произведения
будем называть подмножество декартового произведения 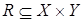 .
.
Пример. Отношение принадлежности (определяет связь между множеством и его элементами, обозначается 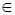 ); отношение включения (определяет связь между двумя множествами); отношение равенства (=); отношение неравенства (
); отношение включения (определяет связь между двумя множествами); отношение равенства (=); отношение неравенства ( 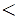 или
или 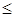 ).
).
Примеры бинарных отношений.
1. Выражения: «быть братом», «делиться на какое-либо число»; «входить в состав (чего-либо)».
2. Всё множество  есть отношение множеств
есть отношение множеств  и
и  .
.
3. Если  - множество действительных чисел, то {
- множество действительных чисел, то { 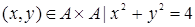 }.
}.
4. Пусть  - множество товаров в магазине, а
- множество товаров в магазине, а  - множество действительных чисел. Тогда
- множество действительных чисел. Тогда 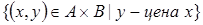 - отношение множеств
- отношение множеств  и
и  .
.
5. Отношение « 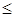 » выполняется для пар (7,9) и (7,7), но не выполняется для пары (9,7).
» выполняется для пар (7,9) и (7,7), но не выполняется для пары (9,7).
6. Если  - множество людей, то
- множество людей, то 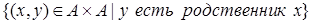 .
.
Для любого бинарного отношения можно записать соответствующее ему соотношение. В общем виде соотношение можно записать как 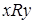 , где
, где  - отношение, устанавливающее связь между элементом
- отношение, устанавливающее связь между элементом  из множества
из множества 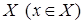 и элементом
и элементом  из множества
из множества 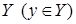 .
.
Определение. Пусть 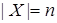 ,
, 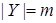 ,
, 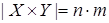 . На паре множеств
. На паре множеств  и
и  можно построить
можно построить 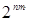 бинарных отношений.
бинарных отношений.
Определение.На множестве  , состоящем из
, состоящем из  элементов, может быть задано
элементов, может быть задано 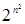 бинарных отношений.
бинарных отношений.
В дальнейшем будем рассматривать бинарные отношения, поэтому вместо термина «бинарное отношение» будем употреблять термин «отношение».
3.3 Область определения и область значений отношений
Определение.
Область определения отношения  на
на 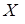 и
и  (обозначим
(обозначим 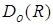 ) есть множество всех
) есть множество всех 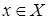 таких, что для некоторых
таких, что для некоторых 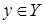 имеем
имеем 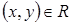 , т.е. область определения
, т.е. область определения  есть множество первых координат упорядоченных пар из
есть множество первых координат упорядоченных пар из  . Область значений отношения
. Область значений отношения  на
на 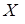 и
и  (обозначим
(обозначим 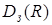 ) есть множество всех
) есть множество всех 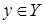 таких, что
таких, что 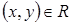 для некоторого
для некоторого 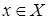 , т.е. область значений есть множество всех вторых координат упорядоченных пар из
, т.е. область значений есть множество всех вторых координат упорядоченных пар из  .
.
Пример.
В примерах отношений, приведенных выше, в частности, в (2), область определения есть все множество  , а область значений - все множество
, а область значений - все множество  . В (3) как область определения, так и область значений совпадают с множеством
. В (3) как область определения, так и область значений совпадают с множеством 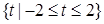 . В (4) область определения есть множество
. В (4) область определения есть множество  , а область значений есть множество всех действительных чисел, каждое из которых совпадает с ценой некоторого товара в магазине. В (6) область определения и область значений есть множество всех людей, имеющих родственников.
, а область значений есть множество всех действительных чисел, каждое из которых совпадает с ценой некоторого товара в магазине. В (6) область определения и область значений есть множество всех людей, имеющих родственников.
Пример. 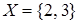 и
и 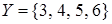 . Декартово произведение этих множеств
. Декартово произведение этих множеств 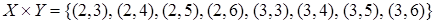 .
.
Отношение «быть делителем» есть множество 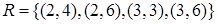 . Отношение «равенство (=)» есть множество
. Отношение «равенство (=)» есть множество 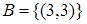 . Отношение «
. Отношение « 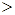 » есть пустое множество
» есть пустое множество 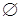 .
.
Области определения и значений отношения  - это соответственно множества
- это соответственно множества 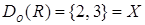 и
и 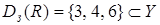 .
.
Области определения и значений отношения  - это соответственно множества
- это соответственно множества 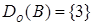 , и
, и 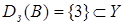 .
.
Определение.Если 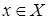 и
и 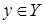 , то
, то  и
и  . В таких случаях
. В таких случаях  есть отношение от
есть отношение от  к
к  , называется соответствиеми обозначается
, называется соответствиеми обозначается  . Если
. Если 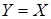 , то любое
, то любое 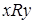 является подмножеством множества
является подмножеством множества 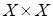 и называется отношением в
и называется отношением в  . Если область определения отношения совпадает с некоторым множеством
. Если область определения отношения совпадает с некоторым множеством 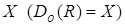 , то говорят, что отношение определенона
, то говорят, что отношение определенона  .
.
Существует три частных случая отношений в  :
:
- полное (универсальное отношение) 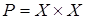 , которое имеет место для каждой пары
, которое имеет место для каждой пары 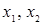 элементов из
элементов из 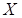 (например, отношение «работать в одном отделе» на множестве сотрудников данного отдела);
(например, отношение «работать в одном отделе» на множестве сотрудников данного отдела);
- тождественное (диагональное) отношение, равносильное  (например, равенство на множестве действительных чисел);
(например, равенство на множестве действительных чисел);
- пустое отношение, которому не удовлетворяет ни одна пара элементов из  (например, отношение «быть братом» на множестве женщин).
(например, отношение «быть братом» на множестве женщин).
3.4 Способы задания отношений
Существует несколько способов задания отношений:
- способ перечисления элементов (в виде списка);
- способ задания характеристического свойства или (порождающей процедуры), выраженного в словесной или символической форме;
- матричный способ;
- графический способ (с помощью ориентированного графа);
- с помощью фактор-множества.
Отношение полностью определяется множеством всех пар элементов 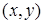 , для которых оно имеет место. Поэтому любое бинарное отношение
, для которых оно имеет место. Поэтому любое бинарное отношение  можно рассматривать как множество упорядоченных пар
можно рассматривать как множество упорядоченных пар 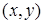 и задавать его в виде списка этих пар
и задавать его в виде списка этих пар 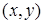 .
.
Пример. На множествах чисел 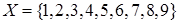 и
и 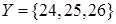 построим отношение «делитель» (
построим отношение «делитель» (  ), которое состоит из упорядоченных пар вида
), которое состоит из упорядоченных пар вида 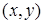 , где
, где  - делитель
- делитель 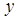 ,
, 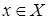 ,
, 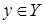 :
:
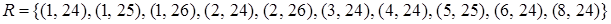 .
.
Часто отношение задается при помощи характеристического свойства, выраженного в словесной или символической форме.
Пример. Пусть  - множество женщин,
- множество женщин,  - множество мужчин. Тогда отношение
- множество мужчин. Тогда отношение  , заданное при помощи характеристического свойства, выраженного в словесной форме, будет иметь вид
, заданное при помощи характеристического свойства, выраженного в словесной форме, будет иметь вид 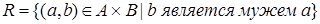 .
.
Пример. Если  - множество действительных чисел, то
- множество действительных чисел, то 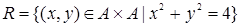 .
.
Матричный способ задания отношений основан на представлении отношения соответствующей ему прямоугольной таблицей (матрицей). Её строки соответствуют первым координатам, а столбцы – вторым координатам. На пересечении 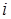 -ой строки и
-ой строки и 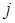 -ого столбца ставится единица, если выполнено соотношение
-ого столбца ставится единица, если выполнено соотношение 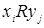 , и нуль, если это соотношение не выполняется (нулевые клетки можно оставлять пустыми).
, и нуль, если это соотношение не выполняется (нулевые клетки можно оставлять пустыми).
Эта матрица содержит всю информацию об отношении  .
.
Полному отношению соответствует квадратная матрица, все клетки которой заполнены единицами, тождественному – квадратная матрица, состоящая из нулей, с главной диагональю из единиц, а пустому – квадратная нулевая матрица.
Пример. Пусть заданы 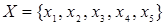 ,
, 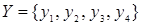 . Отношение
. Отношение 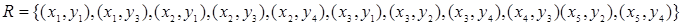 может быть представлено следующей матрицей
может быть представлено следующей матрицей
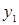 | 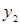 | 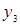 | 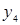 | |
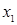 | ||||
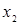 | ||||
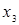 | ||||
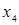 | ||||
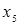 |
Отношения можно задавать (или изображать) с помощью ориентированного графа. Вершины графа соответствуют элементам множеств  и
и  (элементы изображаются точками на плоскости), а дуга, направленная из вершины
(элементы изображаются точками на плоскости), а дуга, направленная из вершины 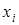 к
к 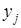 (направленная линия, соединяющая пары точек) означает, что
(направленная линия, соединяющая пары точек) означает, что 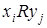 .
.
Пример. Отношение из предыдущего примера представлено в виде следующего ориентированного графа (рис.3.1).

Рисунок 3.1 – Граф отношения 
Отношение в  отображается графом с вершинами, соответствующими элементам этого множества. При этом если имеют место соотношения
отображается графом с вершинами, соответствующими элементам этого множества. При этом если имеют место соотношения 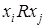 и
и 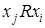 , то вершины связываются двумя противоположно направленными дугами, которые можно условно заменять одной ненаправленной дугой. Соотношению
, то вершины связываются двумя противоположно направленными дугами, которые можно условно заменять одной ненаправленной дугой. Соотношению 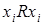 соответствует петля, выходящая из
соответствует петля, выходящая из 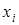 и входящая в эту же вершину.
и входящая в эту же вершину.
Пример. Пусть 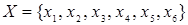 . Отношение
. Отношение 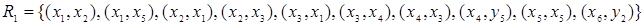 может быть представлено в виде графа на рис. 3.2.
может быть представлено в виде графа на рис. 3.2.
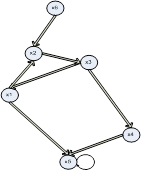
Рисунок 3.2 – Граф отношения 
Пример.
Граф полного отношения для 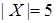 представлен в следующем виде (рис. 3.3).
представлен в следующем виде (рис. 3.3).
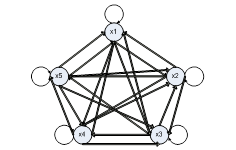
Рисунок 3.3 – Граф полного отношения для 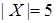
Пример.
Граф тождественного отношения для 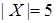 представлен в следующем виде (рис. 3.4).
представлен в следующем виде (рис. 3.4).
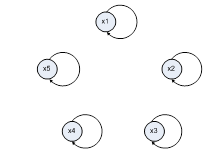
Рисунок 3.4 – Граф тождественного отношения для 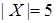
Пример.
Граф пустого отношения для 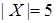 представлен в следующем виде (рис. 3.5).
представлен в следующем виде (рис. 3.5).
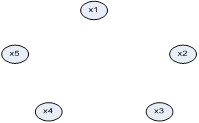
Рисунок 3.5 – Граф пустого отношения для 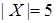
При рассмотрении способа задания отношения с помощью фактор-множества введем понятие сечения отношения.
Определение
Пусть 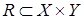 - отношение на множествах
- отношение на множествах  и
и  . Если
. Если 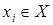 , то сечение отношения
, то сечение отношения  по элементу
по элементу 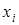 , обозначаемое
, обозначаемое 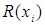 , есть множество
, есть множество 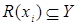 , состоящее из элементов
, состоящее из элементов 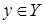 таких, что
таких, что 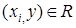 , т.е.
, т.е. 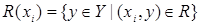 . Множество всех сечений отношения
. Множество всех сечений отношения  называется фактор-множеством множества
называется фактор-множеством множества  по отношению
по отношению  и обозначают
и обозначают  . Объединение сечений по элементам некоторого подмножества
. Объединение сечений по элементам некоторого подмножества 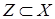 называется сечением R(Z)относительно подмножестваZ.
называется сечением R(Z)относительно подмножестваZ.
Фактор-множество полностью определяет отношение  .
.
Пример. Пусть заданы множества 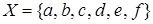 ,
, 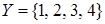 и отношение
и отношение 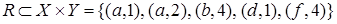 . Получим сечения:
. Получим сечения: 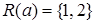 ,
, 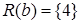 ,
, 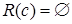 ,
, 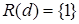 ,
, 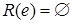 ,
, 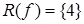 . Определим фактор-множество
. Определим фактор-множество 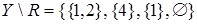 . Рассмотрим множество
. Рассмотрим множество 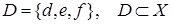 . Сечение отношения
. Сечение отношения  по множеству
по множеству 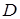 выглядит следующим образом:
выглядит следующим образом: 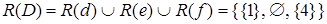 .
.
3.5 Операции над отношениями
Так как отношения – это множества, то над ними могут выполняться все теоретико-множественные операции: объединение, пересечение, дополнение и разность.
Кроме того, определяются специфические для отношений операции: сечение, обращение (симметризация) и композиция.
Рассмотрим два отношения  и
и  , определенные на множествах
, определенные на множествах  и
и  ,
, 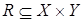 ,
, 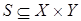 . В результате выполнения операций
. В результате выполнения операций 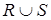 ,
, 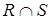 ,
, 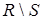 получаем множество упорядоченных пар, являющихся соответственно объединением, пересечением и разностью множеств
получаем множество упорядоченных пар, являющихся соответственно объединением, пересечением и разностью множеств  и
и  . Результаты выполнения этих операций также являются отношениями на множествах
. Результаты выполнения этих операций также являются отношениями на множествах  и
и  . Дополнение отношения
. Дополнение отношения  (обозначается
(обозначается 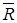 ) содержит все упорядоченные пары множества
) содержит все упорядоченные пары множества  , кроме тех пар, которые принадлежат
, кроме тех пар, которые принадлежат  , т.е.
, т.е. 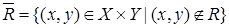 .
.
