Закон исключенного третьего 10 страница

16.6 Распределение разных предметов между одинаковыми урнами при условии, что урны не пусты

Обозначим количество способов разделения n разных предметов между одинаковыми урнами так, чтобы каждая урна была не пустой. Из каждого такого распределения можно получить аналоговых распределений по разным урнам. Таким образом, количество распределений разных предметов между разными урнами с использованием каждой урны в каждом распределении (не пустых урн) равно (5.15).

16.6.1 Числа Моргана

Число носят название чисел Моргана.

Формула выплывает из формулы включений и исключений.

16.6.2 Числа Стирлинга

Числа Стирлинга – комбинаторные понятия, введенные Джеймс‎ом Стирлингом в середине XVIII века. Числа называются числами Стирлинга второго рода. Числам Стирлинга удовлетворяет рекурсивное соотношение .

Число Стирлинга первого рода равно количеству способов представления объектов в виде циклов и обозначается (читается “ циклов из ”).

Например, циклы из 4 элементов и являются одинаковыми. Цикл можно прокручивать, так как его конец соединен с началом.

Пример. Например, существует 11 различных способов составить два цикла из четырех элементов:

Поэтому .

Единичный цикл (цикл, состоящий из одного элемента) – это то же самое, что и единичное множество. 2-цикл подобен 2-множеству, поскольку как и . Однако уже существует два различных 3-цикла: и . Из любого -элементного множества могут быть составлены циклов, если (всего имеется перестановок, а каждый цикл соответствует сразу из них, так как отсчет цикла может быть начат с любого из его элементов). Поэтому

Если все циклы являются единичными или двойными, то Например,

Выведем рекуррентную формулу для вычисления чисел Стирлинга первого рода. Каждое представление объектов в виде циклов либо помещает последний объект в отдельный цикл способами, либо вставляет этот объект в одно из циклических представлений первых 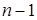объектов. В последнем случае существует 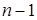различных способов подобной вставки. Например, при вставке элемента 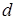в цикл можно получить только 3 разных цикла: . Таким образом, рекуррентность имеет вид

Треугольник Стирлинга для числа циклов

Теорема. Имеет место соотношение

Доказательство. обозначает число перестановок объектов, которое содержит ровно циклов. Если просуммировать по всем , то должно получиться общее число перестановок, равное .

Число Стирлинга второго рода равно количеству способов разбиения множества из элементов на непустых подмножеств и обозначается (читается “ подмножеств из ”).

Пример. Например, существует 7 способов разбиения четырехэлементного множества на две части:

Поэтому .

Рассмотрим значения чисел Стирлинга для малых значений :

1. . Существует только один способ разбиения пустого множества на нулевое число непустых частей, поэтому . Для непустого множества нужна по крайней мере хотя бы одна часть, так что при .

2. . Существует только один способ помещения n элементов в одно-единственное непустое множество, поэтому при . Однако , так как 0-элементное множество пусто.

3. 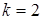. Очевидно, что . Если множество из объектов разделено на две непустые части, то одна из этих частей содержит последний объект и некоторое подмножество из 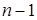объектов. Имеется подмножеств из 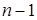объектов. Поскольку все объекты нельзя поместить в одну часть, то .

Треугольник Стирлинга для числа подмножеств.

Выведем рекуррентное соотношение, при помощи которого можно будет вычислить значения . Если задано множество из объектов, которое должно быть разбито на k непустых частей, то мы либо помещаем последний объект в отдельный класс, а оставшиеся 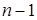объект разбиваем на 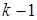часть способами, либо помещаем его в любую из частей, на которые разбиты 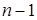объект. В последнем случае имеется возможных вариантов, поскольку каждый из способов распределения первых 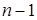объектов по непустым частям дает k подмножеств, с которыми можно объединить объект. Имеем рекуррентную формулу:

16.6.3 Числа Белла

Число Белла равно количеству разбиений множества из элементов на произвольное количество непустых подмножеств, которые не пересекаются. Очевидно, что , так как существует только одно разбиение пустого множества. Например, , так как существует 5 возможных разбиений множества из трех элементов:

.

Заметим, что элементов можно разбить на 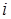множеств . При этом количество разбиений – элементного множества на подмножеств равно числу Стирлинга 2 рода . Откуда получаем формулу .

Рассмотрим следующие конструкции, в которых точки обозначают одноэлементные множества, а сегменты объединяют элементы, принадлежащие одному множеству. Из элементов можно построить разных таких конструкций.

Теорема. Числа Белла удовлетворяют следующему рекуррентному соотношению

Доказательство. Рассмотрим разбиение элемента в зависимости от величины блока, в котором находится – ый элемнент. Пусть размер этого блока равен 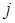. Тогда существует способов выбрать в него кроме – ого еше элемент. Остальные элементов можно разбить способами.Таким образом:

Пример.Например, . Числа Белла удовлетворяют следующему свойству:

Для значений получим следующие значения детерминанта:

1, 1, 2, 12, 288, 34560, 24883200, 125411328000, 5056584744960000, 1834933472251084800000, 6658606584104736522240000000, …

При разложении функции в ряд Маклорена коэффициенты ряда образуют числа Белла:

Числа могут быть построены при помощи треугольника Белла. Первая строка содержит 1. Каждая следующая строка начинается числом, стоящим в конце предыдущей строки. Каждое следующее число в строке равно сумме чиел, стоящих слева и сверху от него. Числа Белла образуют последние числа в строках.

16.7 Композиции

16.7.1 Понятие композиции чисел

При решении задач про распределение одинаковых предметов между непустыми урнами можно говорить о разложении числа в сумму натуральных слагаемых : , где

Два таких разложения числа считаются разными, если они отличаются хотя бы одним слагаемым. В таком случае говорят о композиции числа . В ином случае, композиция числа –это его разложение в виде , где учитываются как величины слагаемых (частей) , так и порядок их расположения в сумме.

Пример. Выписать все композиции числа 3.

Композиции имеют вид3=3, 3=2+1, 3=1+2, 3=1+1+1.

16.7.2 Композиции с ограничениями на количество слагаемых

Число композиций числа из слагаемых равно числу распределений одинаковых предметов по разным урнам при условии отсутствия пустых урн. Число предметов, которые попали в урну с номером 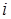, дает слагаемое . Отсюда выплывает, что .

Число всех композиций числа равно .

16.8 Комбинаторика разбиений

При анализе стратегий различных игр требуется подсчитывать количество комбинаций при раскладе определенных предметов. Наиболее распространенная карточная игра – преферанс. В классическом варианте этой игры карты раскладываются на 3 кучки (по числу играющих) и 2 карты кладутся в “прикуп“. Играют 32 картами, т.е. каждый игрок получает по 10 карт.

Определим количество вариантов расклада при игре в преферанс: . Для обоснования полученной формулы расставим все карты подряд и переставим их 32! способами. При каждой перестановке будем выделять первые 10 карт первому игроку, вторую десятку – второму, третью – третьему, а последние 2 карты будем откладывать в “прикуп”. После этого заметим, что перестановка 10 карт в руках каждого игрока не меняет варианта расклада, как и положения 2 карт в прикупе. Поэтому 32! разделим три раза на 10! и еще на 2!. В общем случае, если раскладываются разных предметов по ящикам так, чтобы в 1-й ящик (кучку, игроку в руки) попало предметов, во второй предмета, в -й – предметов, при этом , то число вариантов расклада .

16.9 Контрольные вопросы и задания

1. Какой предварительный анализ содержания задачи необходимо осуществить, чтобы можно было применить урновые схемы решения?

2. Какую формулу необходимо использовать, чтобы решить задачу о распределении разных предметов по урнам?

3. Какую формулу необходимо использовать, чтобы решить задачу о распределении одинаковых предметов по урнам?

4. Какую формулу необходимо использовать, чтобы решить задачу о распределении разных предметов без учета порядка предметов в урнах?

5. Какие формулы необходимо использовать, чтобы решить задачу о распределении разных предметов между одинаковыми урнами при условии, что урны не пустые?

6. В каких комбинаторных задачах используются числа Моргана, Стирлинга, Белла?