Случайные функции. Многомерные законы распределения

Случайной функцией (процессом) называется функция, значения которой при каждом данном значении аргумента являются случайной величиной. В результате опытов случайная функция принимает различные конкретные формы - это реализации случайной функции. Случайную функцию можно рассматривать как бесконечную совокупность случайных величин, зависящих от одного или нескольких непрерывно изменяющихся параметров. Случайные функции времени называются стохастическими процессами. Случайный процесс не есть определенная кривая (рис.61). Это такая функция времени, значения которой в каждый момент времени являются случайной величиной. Предсказать протекание одной реализации случайного процесса нельзя. Можно сделать лишь предсказание статистического характера относительно множества реализ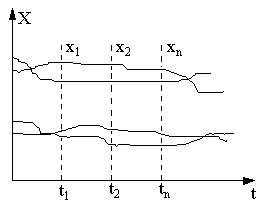а-

Рис.61. Реализации случайного процесса

ций, протекающих в одинаковых условиях, т.е. случайный процесс может быть оценен некоторыми вероятностными характеристиками, например, законами распределения. Так как при каждом данном значении аргумента t значение случайной функции x(t) является случайной величиной, то полной вероятностной характеристикой этого значения является его закон распределения, который называется одномерным законом распределения. Этот закон зависит от t как от параметра и может быть задан одномерной плотностью вероятности f(x,t). Это функция времени, ибо вероятностное распределение с течением времени может меняться.

Произведение f(x,t)dx дает вероятность того, что в момент времени t величина X находится в интервале (x<X<x+dx). Эту величину можно найти приближенно экспериментальным путем, если наблюдать в момент времени t ряд систем, находящихся в одинаковых условиях. Для каждого данного t в отдельности будет свой закон распределения, причем для каждого из них

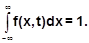
Одномерный закон распределения случайной функции является достаточной характеристикой случайной функции для тех задач, в которых значения случайной функции при различных значениях аргумента рассматриваются изолировано друг от друга. Для того, чтобы определить связь между возможными значениями случайной функции x(t) в различные моменты времени, вводится двумерный закон распределения, который задается двумерной плотностью вероятности: f(x₁,x₂,t₁,t₂). Это характеристика системы двух случайных величин x(t₁), x(t₂)- двух сечений случайной функции x(t) в произвольные моменты времени t₁ и t₂.