Основные логические операции.
При построении узлов ЭВМ используются комбинационные схемы, основанные на использовании алгебры логики, а точнее на использовании булевых функций. Функция от двоичных переменных называется булевой, если она, так же как ее аргументы, принимает только два значения 0 или 1. При помощи булевых функций в компьютере реализуются логические операции над двоичными переменными. Соответствующие схемы называются комбинационными логическими элементами.
Рассмотрим основные логические операции и соответствующие им логические элементы, предназначенные для построения цифровых устройств компьютера.
Отрицание (инверсия), от латинского inversio –переворачиваю, соответствует частице НЕ, словосочетанию НЕВЕРНО, ЧТО;
_
Обозначение: не A, A, -A;
Таблица истинности:
| A | _ A |
Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.
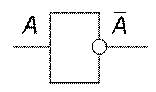 |
Логическая схема (инвертор):
Логическое умножение (конъюкция), от латинского conjunctio –связываю, соответствует союзу И (в естественном языке: и А, и В,)
Обозначение: ×, •, &, и, 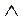 , and.
, and.
Таблица истинности:
| A | B | A 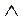 B B |
Конъюкция истинна тогда и только тогда, когда оба высказывания истинны.
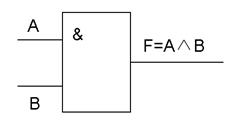 |
Логическая схема (конъюктор):
Логическое сложение (дизъюнкция), от латинского disjunctio - различаю: соответствует союзу ИЛИ;
Обозначение: +, или, or, 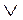 .
.
Таблица истинности:
| A | B | A 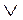 B B |
Дизъюнкция ложна тогда и только тогда, когда оба высказывания ложны.
 |
Логическая схема (дизъюнктор)
Импликация (логическое следование), от латинского implicato - тесно связываю соответствует речевому обороту ЕСЛИ....ТО
Обозначение: →;
Таблица истинности:
| A | B | A→B |
Импликация истинна всегда, за исключением случая, когда А истинно, а В ложно.
Эквиваленция (равнозначность), от латинского aequivalens – равноценные соответствует речевым оборотам ЭКВИВАЛЕНТНО:
Обозначение: =, ↔;
Таблица истинности:
| A | B | A↔B |
Эквиваленция истинна тогда и только тогда, когда оба высказывания одновременно либо истинны, либо ложны.
Порядок выполнения логических операций:
1. операция в скобках;
2. отрицание;
3. логическое умножение;
4. логическое сложение;
5. импликация;
6. эквиваленция.
Любое сложное высказывание можно записать с помощью основных логических операций И, ИЛИ, НЕ.
Рассмотрим пример. При каких A и B логическая функция 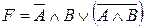 принимает значение ложь (0)?
принимает значение ложь (0)?
Составим таблицу истинности логической функции F
| A | B | 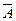 | 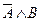 | 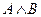 | 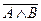 | 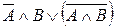 |
Из таблицы видно, что логическая функция F принимает значение 0 только при A=1 и B=1.
С помощью логических схем И, ИЛИ, НЕ можно реализовать логическую функцию, описывающую работу различных устройств компьютера.
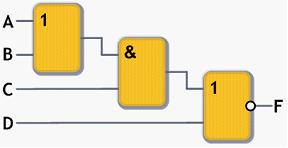
Рассмотрим пример. При какой комбинации сигналов (А, В, С, D) на входе логической схемы F=1. …
 |
 |
Для определения состояний сигнала на входе логической схемы необходимо рассмотреть ее отдельные элементы.
1) Схема И реализует конъюнкцию двух или более логических значений. Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Если хотя бы на одном входе будет ноль, на выходе также будет ноль. Условное графическое изображение логического элемента представлено на рисунке
 |
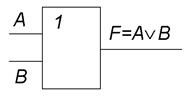
2) Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Единица на выходе схемы ИЛИбудет тогда и только тогда, когда на любом из входов будет единица. Если на обоих входах будет ноль, на выходе также будет ноль. Условное графическое изображение логического элемента представлено на рисунке
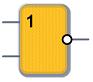 |
3) Схема ИЛИ-НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Единица на выходе схемы ИЛИ-НЕ будет тогда и только тогда, когда на обоих входах будет ноль. Условное графическое изображение логического элемента представлено на рисунке
Подставляя различные комбинации сигналов для А, В, С и D, мы определяем тот вариант, который дает на выходе логической схемы значение 1 (True). Это будет, например комбинация A=1, B=1, C=0, D=0.
