Оценивание неисключенной систематической погрешности и стандартной неопределенности, оцениваемой по типу В, результата измерения

6.1 НСП результата измерения выражают границами этой погрешности, если среди составляющих погрешности результата измерения в наличии одна НСП.

При указанном выше условии стандартную неопределенность u_В, обусловленную неисключенной систематической погрешностью, заданной своими границами ± Q, оценивают по формуле (2).

6.2 Доверительные границы НСП результата измерения вычисляют следующим образом.

6.2.1 При наличии нескольких НСП, заданных своими границами ± Q_j, доверительную границу НСП результата измерения Q(Р) (без учета знака) вычисляют по формуле

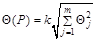, (5)

где k — поправочный коэффициент, определяемый принятой доверительной вероятностью и числом m составляющих Q_j.

При доверительной вероятности Р = 0,95 поправочный коэффициент k принимают равным 1,1.

При доверительной вероятности Р = 0,99 поправочный коэффициент k принимают равным 1,45, если число суммируемых составляющих m > 4. Если же число составляющих равно четырем (m = 4), то поправочный коэффициент k » 1,4; при m = 3 k » 1,3; при m = 2 k » 1,2. Более точное значение k для доверительной вероятности Р = 0,99 при числе составляющих m £ 4 в зависимости от соотношения составляющих I определяют по графику [k = f(m, l)] в соответствии с требованиями ГОСТ 8.207.

Примечание — Погрешность, возникающая при использовании формулы (5) для суммирования НСП и при нахождении поправочного коэффициента k для доверительной вероятности Р = 0,99 по графику [(k = f(m, l)], не превышает 5 %.

При условии, указанном в 6.2.1, суммарную стандартную неопределенность, оцениваемую по типу В, u_{с, B} вычисляют по формуле

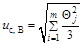. (6)

6.2.2 При наличии нескольких НСП, заданных доверительными границами Q_j (Р_i), рассчитанными по формуле (5), доверительную границу НСП результата однократного измерения вычисляют по формуле

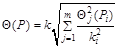. (7)

При условии, указанном выше, суммарную стандартную неопределенность, оцениваемую по типу В, вычисляют по формуле

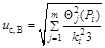, (8)

где Q_j(P_i) — доверительная граница j-й НСП, соответствующая доверительной вероятности Р_i;

k и k_i — коэффициенты, соответствующие доверительным вероятностям Р и Р_i.

Значения коэффициентов k и k_i определяют в соответствии с требованиями 6.2.1.