Классификация погрешностей измерения по причине возникновения и полноте охвата измерительной задачи
1. По причинам появления можно выделить следующие погрешности: методические, инструментальные и субъективные.Методические погрешности обусловлены несовершенством метода измерения, допущениями и упрощениями при использовании эмпирических зависимостей и др. Они закладываются и известны на стадии проектирования, например погрешность, связанная с ценой деления. Все методические погрешности для приборов одного типа всегда одинаковы. Отличительная особенность методических погрешностей – то, что они могут быть определены лишь путем создания математической модели, или имитационным моделированием измеряемого объекта и не могут быть найдены при сколь угодно тщательном исследовании лишь самого измерительного прибора. Если при проектировании прибора сделаны какие-то допущения, округления, приближения, то они приведут к погрешности уже в уравнении измерения или в статистической характеристике прибора. Например, при измерении мощности методом детектирования подразумевается, что характеристика детектора квадратичная на начальном участке и линейная при больших сигналах. Реальная характеристика отличается от принятой модели. Методическая погрешность может быть также обусловлена влиянием измерительного устройства на измеряемую величину. Примером может служить погрешность шунтирования, возникающая при измерении напряжения вольтметром. Вследствие шунтирования входным сопротивлением вольтметра того участка цепи, на котором измеряется напряжение, оно оказывается меньше, чем было до присоединения вольтметра. Поэтому для одного и того же вольтметра,
присоединяемого поочередно к разным участкам исследуемой цепи, эта погрешность различна: на низкоомных участках – ничтожна, а на высокоомных может быть очень большой.
Размер этой переменной погрешности не может быть указан в паспорте прибора, и она является методической. Для расчета этой погрешности пользователь должен при каждом конкретном измерении напряжения оценивать сопротивление исследуемой цепи между точками, к которым присоединен вольтметр, т.е. проводить дополнительное исследование объекта измерения. Часто причиной возникновения методической погрешности является то, что, организуя измерения, нередко измеряют или вынуждены измерять не ту величину, которая в принципе должна быть измерена, а некоторую другую, близкую, но неравную ей. Этот прием замены позволяет создавать наиболее простые, надежные и универсальные приборы. Когда метод уже воплощен в приборе, то его погрешности должны быть изучены, определены и занесены в паспорт. С этого момента вне зависимости от причин возникновения погрешности для пользователя могут считаться инструментальными. Инструментальные погрешности обусловлены свойствами средств измерений: неидеальностью составных частей, несовершенством технического процесса изготовления прибора и разбросом параметров элементов. К этим погрешностям относят также погрешности, связанные с влиянием внешних факторов и режима питания. Субъективные погрешности обусловлены влиянием на результаты оператора, снимающего показания (например погрешность параллакса).
15. Математические модели и характеристики погрешностей
Математические модели и характеристики
погрешностей
В общем случае результаты измерений и их погрешности должны рассматриваться как функции, изменяющиеся во времени случайным образом, т.е. случайные функции, или, как принято говорить в математике, случайные процессы. Поэтому математическое описание результатов и погрешностей измерений (т.е. их математические модели) должно строиться на основе теории случайных процессов [48, 49]. Без этого невозможно решение большого числа практических метрологических задач. Прежде чем перейти к рассмотрению математических моделей погрешностей измерений, кратко изложим основные моменты теории случайных функций.
Случайным процессом X(t) называется процесс (функция), значение которого при любом фиксированном значении t = tQ является случайной величиной X(t0). Конкретный вид процесса (функции), полученный в результате опыта, называетсяреализацией. При проведении серии опытов можно получить группу или семейство реализаций случайной функции (рис. 4.5). Семейство реализаций случайного процесса является основным экспериментальным материалом, на основе которого можно получить его характеристики и параметры.
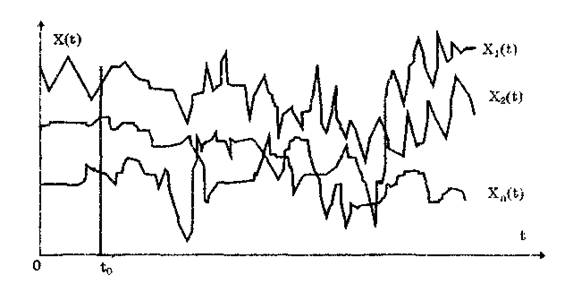
Рис. 4.5. Вид случайных функций
Каждая реализация является неслучайной функцией времени. Семейство реализаций при каком-либо фиксированном значении времени t0 (см. рис. 4.5) представляет собой случайную величину, называемую сечением случайной функции,соответствующим моменту времени tQ. Следовательно, случайная функция совмещает в себе характерные признаки случайной величины и детерминированной функции. При фиксированном значении аргумента она превращается в случайную величину, а в результате каждого отдельного опыта становится детерминированной функцией.
Наиболее полно случайные процессы описываются законами распределения: одномерным, двумерным и т.д. Однако оперировать с такими, в общем случае многомерными функциями очень сложно, поэтому в инженерных приложениях, каковым является метрология, стараются обойтись характеристиками и параметрами этих законов, которые описывают случайные процессы не полностью, а частично. Характеристики случайных процессов, в отличие от характеристик случайных величин, которые подробно рассмотрены в гл. 6, являются не числами, а функциями. К важнейшим из них относятся математическое ожидание и дисперсия.
Математическим ожиданием случайной функции X(t) называется неслучайная функция
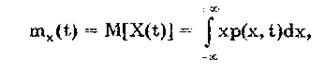
которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения. Здесь p(x,t) — одномерная плотность распределения случайной величины х в соответствующем сечении случайного процесса X(t).Таким образом, математическое ожидание в данном случае является средней функцией, вокруг которой группируются конкретные реализации.
Дисперсией случайной функции X(t) называется неслучайная функция
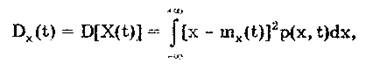
значение которой для каждого момента времени равно дисперсии соответствующего сечения, т.е. дисперсия характеризует разброс реализаций относительно mx(t).
Математическое ожидание случайного процесса и его дисперсия являются весьма важными, но не исчерпывающими характеристиками, так как определяются только одномерным законом распределения. Они не могут характеризовать взаимосвязь между различными сечениями случайного процесса при различных значениях времени t и t'. Для этого используется корреляционная функция — неслучайная функция R(t, t') двух аргументов t и t', которая при каждой паре значений аргументов равна ковариации соответствующих сечений случайного процесса:
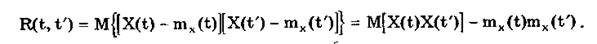
Корреляционная функция, называемая иногда автокорреляционной, описывает статистическую связь между мгновенными значениями случайной функции, разделенными заданным значением времени т = t'-t. При равенстве аргументов корреляционная функция равна дисперсии случайного процесса. Она всегда неотрицательна.
На пpaктике часто используется нормированная корреляционная функция
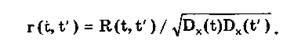
Она обладает следующими свойствами: 1) при равенстве аргументов t и t' r(t,t') = 1; 2) симметрична относительно своих аргументов: r(t,t') = r(t',t); 3) ее возможные значения лежат в диапазоне [-1; 1], т.е. |r(t,t')| < 1. Нормированная корреляционная функция по смыслу аналогична коэффициенту корреляции между случайными величинами, но зависит от двух аргументов и не является постоянной величиной.
Случайные процессы, протекающие во времени однородно, частные реализации которых с постоянной амплитудой колеблются вокруг средней функции, называютсястационарными. Количественно свойства стационарных процессов характеризуются следующими условиями.
• Математическое ожидание стационарного процесса постоянно, т.е.
m (t) = mx = const. Однако это требование не является существенным, поскольку от случайной функции X(t) всегда можно перейти к центрированной функции, для которой математическое ожидание равно нулю. Отсюда вытекает, что если случайный процесс нестационарен только за счет переменного во времени (по сечениям) математического ожидания, то операцией центрирования его всегда можно свести к стационарному.
• Для стационарного случайного процесса Дисперсия по сечениям является постоянной величиной, т.е. Dx(t) = Dx = const.
• Корреляционная функция стационарного процесса зависит не от значения аргументов t и t', а только от промежутка t = t' - t, т.е. R(t,t') = R(t). Предыдущее условие является частным случаем данного условия, т.е. Dx(t) = R(t,t) = R(t = 0) = const.
Таким образом, зависимость автокорреляционной функции только от интервала tявляется единственным существенным условием стационарности случайного процесса.
Важной характеристикой стационарного случайного процесса является его спектральная плотность S(w), которая описывает частотный состав случайного процесса при w > О и выражает среднюю мощность случайного процесса, приходящуюся на единицу полосы частот:
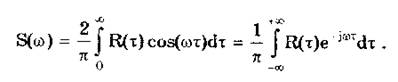
Спектральная плотность стационарного случайного процесса является неотрицательной функцией частоты S(w) ³ 0. Площадь, заключенная под кривой S(w), пропорциональна дисперсии процесса.
Корреляционная функция может быть выражена через спектральную плотность
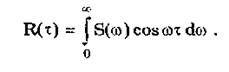
Стационарные случайные процессы могут обладать или не обладать свойством эргодичности. Стационарный случайный процесс называется эргодическим, если любая его реализация достаточной продолжительности является как бы "полномочным представителем" всей совокупности реализаций процесса. В таких процессах любая реализация рано или поздно пройдет через любое состояние независимо от того, в каком состоянии находился этот процесс в начальный момент времени.
Для эргодического стационарного случайного процесса его математическое ожидание может быть определено из выражения
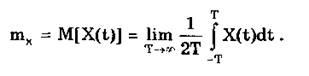
Достаточным условием выполнения этого равенства — эргодичности стационарного случайного процесса X(t) по математическому ожиданию — является выполнение условия 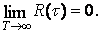
Дисперсия эргодического процесса может быть найдена по формуле
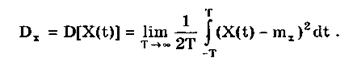
Достаточным условием выполнения этого равенства — эргодичности стационарного процесса X(t) по дисперсии — является
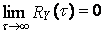 , где RY(t) — корреляционная функция стационарного случайного процесса Y(t) = [X(t)]2 .
, где RY(t) — корреляционная функция стационарного случайного процесса Y(t) = [X(t)]2 .
Корреляционная функция стационарного эргодического случайного процесса может быть определена по формуле
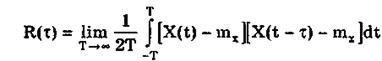
Достаточным условием выполнения последнего равенства — эргодичности стационарного процесса X(t) по корреляционной функции — является
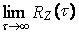 , где RZ(t) — корреляционная функция стационарного случайного процессаZ (t, q) = X(t) X(t + q).
, где RZ(t) — корреляционная функция стационарного случайного процессаZ (t, q) = X(t) X(t + q).
При построении математической модели погрешности измерений следует учитывать всю информацию о проводимом измерении и его элементах. Модели для измерений, проводимых различными методами и средствами, могут существенно различаться.
В общем случае абсолютную погрешность измерения Д(1) следует представлять [7, 58] в виде суммы нескольких составляющих:
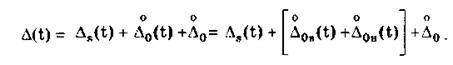
Каждая из них может быть обусловлена действием нескольких различных источников погрешностей и в свою очередь состоять также из некоторого числа составляющих.̊
Систематическая составляющая  D̊(t) представляет собой нестационарную случайную функцию, описывающую постоянную или инфра-низкочастотную погрешность, причины возникновения которой могут быть различными. Периоды изменения составляющих систематической погрешности значительно больше времени, необходимого для проведения измерения. Поэтому погрешность \(t) условно принимается за постоянную и для ее учета применяются математические методы, разработанные для неизменных во времени и от измерения к измерению погрешностей, значения которых неизвестны.
D̊(t) представляет собой нестационарную случайную функцию, описывающую постоянную или инфра-низкочастотную погрешность, причины возникновения которой могут быть различными. Периоды изменения составляющих систематической погрешности значительно больше времени, необходимого для проведения измерения. Поэтому погрешность \(t) условно принимается за постоянную и для ее учета применяются математические методы, разработанные для неизменных во времени и от измерения к измерению погрешностей, значения которых неизвестны.
Составляющая D̊(t) является случайной и имеет широкий частотный спектр. Периоды изменения составляющих этой погрешности меньше или сравнимы со временем измерения. Она может быть разделена на две составляющие: D̊0в(t) и D̊0н(t), которые являются стационарными случайными функциями времени с различными частотными спектрами — высокочастотным и низкочастотным соответственно. Автокорреляционная функция высокочастотной составляющей погрешности затухает в течение времени, значительно меньшего времени измерения. Для низкочастотной составляющей автокорреляционная функция затухает до нуля в течение времени, большего времени отдельного измерения. Такое различие в поведении этих составляющих обуславливает их выделение и применение к ним различных методик обработки.
Составляющая D̊0 является центрированной случайной величиной, не зависящей от времени, но изменяющейся от измерения к измерению. Величины D̊0в(t) и D̊0 могут быть объединены в одну стационарную центрированную функцию D̊(t). Ее автокорреляционная функция затухает на интервале времени, который меньше времени проведения всего измерения, но существенно больше интервала времени, необходимого для одного измерения. В связи с этим математическая модель погрешности измерения может быть записана в виде
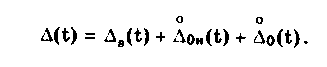
Отдельные составляющие этого уравнения могут отсутствовать при моделировании погрешности конкретного измерения. Так, зачастую нет необходимости учитывать высокочастотную составляющую погрешности измерения.
Эффективное использование рассмотренной модели погрешности измерения возможно только при известном частотном спектре ее составляющих. Однако данное условие весьма трудно выполнить на практике, и поэтому часто случайная погрешность измерения описывается не случайной функцией, а представляется еще в более упрощенном виде, а именно в виде случайной величины. При этом для описания погрешностей используются теория вероятностей и математическая статистика. Однако прежде необходимо сделать ряд существенных оговорок:
• применение методов математической статистики к обработке результатов измерений правомочно лишь в предположении о независимости между собой отдельных получаемых отсчетов;
• большинство используемых в метрологии формул теории вероятностей правомерны только для непрерывных распределений, в то время как распределения погрешностей вследствие неизбежного квантования отсчетов, строго говоря, всегда дискретны, т.е. погрешность может принимать лишь счетное множество значений.
Таким образом, условия непрерывности и независимости для результатов измерений и их погрешностей соблюдаются приближенно, а иногда и не соблюдаются. В математике под термином "непрерывная случайная величина" понимается существенно более узкое, ограниченное рядом условий понятие, чем "случайная погрешность" в метрологии.
С учетом этих ограничений процесс появления случайных погрешностей результатов измерений за вычетом систематических и прогрессирующих погрешностей обычно может рассматриваться как центрированный стационарный случайный процесс. Его описание возможно на основе теории статистически независимых случайных величин и стационарных случайных процессов.
При выполнении измерений требуется количественно оценить погрешность. Для такой оценки необходимо знать определенные характеристики и параметры модели погрешности. Их номенклатура зависит от вида модели и требований к оцениваемой погрешности. В метрологии принято различать три группы характеристик и параметров погрешностей. Первая группа — задаваемые в качестве требуемых или допускаемых нормы характеристик погрешности измерений (нормы погрешностей). Вторая группа характеристик — погрешности, приписываемые совокупности выполняемых по определенной методике измерений. Характеристики этих двух групп применяются в основном при массовых технических измерениях и представляют собой вероятностные характеристики погрешности измерений. Третья группа характеристик — статистические оценки погрешностей измерений отражают близость отдельного, экспериментально полученного результата измерения к истинному значению измеряемой величины. Они используются в случае измерений, проводимых при научных исследованиях и метрологических работах.
В качестве характеристик случайной погрешности используют СКО случайной составляющей погрешности измерений и, если необходимо, ее нормализованную автокорреляционную функцию.
Систематическая составляющая погрешности измерений характеризуется:
• СКО неисключенной систематической составляющей погрешности измерений;
• границами, в которых неисключенная систематическая составляющая погрешности измерений находится с заданной вероятностью (в частности, и с вероятностью, равной единице).
Требования к характеристикам погрешности и рекомендации по их выбору приведены в нормативном документе МИ 1317-86 "ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров".
16. Принципы оценивания погрешностей
Принципы оценивания погрешностей
Оценивание погрешностей производится с целью получения объективных данных о точности результата измерения. Точность результата измерения характеризуется погрешностью. Погрешность измерения описывается определенной математической моделью, выбор которой обуславливается имеющимися априорными сведениями об источниках погрешности, а также данными, полученными в ходе измерений. С помощью выбранной модели определяются характеристики и параметры погрешности, используемые для к-оли-чественного выражения тех или иных ее свойств.
Характеристики погрешности принято делить на точечные и интервальные. Кточечным относятся СКО случайной погрешности и предел сверху для модуля систематической погрешности, к интервальным — границы неопределенности результата измерения. Если эти границы определяются как отвечающие некоторой доверительной вероятности, то они называются доверительными интервалами. Если же минимально возможные в конкретном случае границы погрешности оценивают так, что погрешность, выходящую за них, встретить нельзя, то они называютсяпредельными (безусловными) интервалами.
В основу выбора оценок погрешностей положен ряд принципов. Во-первых, оцениваются отдельные характеристики и параметры выбранной модели погрешности. Это связано с тем, что модели погрешностей, как правило, сложны и описываются многими параметрами. Определение их всех весьма затруднительно, а иногда и невозможно. Кроме этого, в большинстве практических случаев полное описание модели погрешности содержит избыточную информацию, в то время как знание отдельных ее характеристик вполне достаточно для достижения цели измерения. Во-вторых, оценки погрешности определяют приближенно, с точностью, согласованной с целью измерения. Это обусловлено тем, что погрешности определяют лишь зону неопределенности результата измерения и их не требуется знать очень точно. В-третьих, погрешности оцениваются сверху, поэтому погрешность лучше преувеличить, чем преуменьшить, так как в первом случае снижается качество измерений, а во втором — возможно полное обесценивание результатов всего измерения. В-четвертых, поскольку стремятся получить реалистические значения оценки погрешности результата измерения, т.е. не слишком завышенные и не слишком заниженные, точность измерений должна соответствовать цели измерения. Излишняя точность ведет к неоправданному расходу средств и времени. Недостаточная точность в зависимости от цели измерения может привести к признанию годным в действительности негодного изделия, к принятию ошибочного решения и т. п.
Оценивание погрешностей может проводится до (априорное) и после (апостериорное) измерения. Априорное оценивание — это проверка возможности обеспечить требуемую точность измерений, проводимых в заданных условиях выбранным методом с помощью конкретных СИ. Оно проводится в случаях:
• нормирования метрологических характеристик СИ;
• разработки методик выполнения измерений;
• выбора средств измерений для решения конкретной измерительной задачи;
• подготовки измерений, проводимых с помощью конкретного СИ.
Апостериорную оценку проводят в тех случаях, когда априорная оценка неудовлетворительна или получена на основе типовых метрологических характеристик, а требуется учесть индивидуальные свойства используемого СИ. Такую оценку следует рассматривать как коррекцию априорных оценок.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
принципы оценивания погрешностей.
Характеристики погрешностей принято делить на точечные и интервальные.
К точечным относятся: СПО (случайная погрешность), мат. ожидание, дисперсия. К интервальным — границы неопределенностей результатов измерения.
Оценивание погрешностей может проводиться до (априорное) и после (апостериорное) измерения.
Априорное оценивание — это проверка возможностей обеспечить требуемую точность измерений, проводимых в заданных условиях выбранным методом с помощью конкретных средств измерения. Оно проводится в следующих случаях:
1. нормирование метрологических характеристик средств измерения;
2. разработка методик выполнения измерений;
3. выборы средства измерения для решения конкретной измерительной задачи;
4. подготовка измерений, проводимых с помощью конкретного средства измерения.
Апостериорная оценка проводится в тех случаях, когда априорное оценивание неудовлетворительно или получено на основе типовых метрологических характеристик, а требуется учесть индивидуальные свойства используемых средств измерения.
17. Обнаружение и устранение систематических погрешностей
Способы обнаружения и устранения систематических погрешностей.
Пути исключения систематических погрешностей:
1) Устранение источников погрешностей до начала измерений.
2) Определение поправок и внесение их в результат измерения.
3) Оценка границ неисключенных систематических погрешностей.
Результат одного измерения:
Xi = Xu + Di + Qi
где Xu — истинное значение измеряемой величины,
Di — i-ая случайная погр-ть,
Qi — систематическая погр-ть.
После усреднения результатов многократных измерений получаем среднее арифметическое значение измеряемой величины:
Если Qi = Q, то
Систематические погрешности принято классифицировать в
зависимости от причин их возникновения и по характеру их проявления
при измерениях.
При проведении измерений стараются в максимальной степени
исключить или учесть влияние систематических погрешностей. Для того
чтобы исключить систематические погрешности при измерении,
необходимо проанализировать всю совокупность опытных данных.
Поскольку приемы измерения различных величин разнообразны,
постольку различны и приемы исключения систематических
погрешностей. Дать исчерпывающие правила для отыскания и
исключения систематических погрешностей невозможно.
Наиболее распространенные способы исключения систематических
погрешностей из результатов измерений следующие.
1. Устранение источников погрешностей до начала измерения.
Этот способ исключения систематических погрешностей является
наиболее рациональным, так как он полностью или частично освобождает
от необходимости устранять погрешности в процессе измерения или
вычислять результат с учетом поправок. Под устранением источника14
погрешностей следует понимать как непосредственное его удаление
(например, удаление источника тепла), так и защиту измерительной
аппаратуры и объекта измерения or влияния этих источников.
Устранение влияния температуры осуществляется применением
термостатирования, т.е. обеспечением определенной температуры
окружающей среды. Термостатируют большие помещения (цеха,
лаборатории), небольшие помещения (комнаты, камеры), средства
измерений в целом или их отдельные части (катушки сопротивления,
нормальные элементы, свободные концы термопар, кварцевые
стабилизаторы частоты и т. п.). В настоящее время термостатирование во
многих случаях заменяют кондиционированием воздуха. При
кондиционировании обеспечивается поддержание на требуемом уровне не
только температуры, но и других параметров окружающего воздуха и в
первую очередь влажности.
Устранение влияния магнитных полей достигается устройством
замкнутых и непрерывных экранов из магнитомягких материалов.
Магнитные силовые линии должны огибать экранируемое пространство.
Устранение вредных вибраций и сотрясений достигается путем
амортизации средства измерений и его деталей. Для амортизации
используют различного рода поглотители колебаний, например, губчатую
резину в сочетании с различного рода эластичными подвесами (струны,
пружины).
Устранение других видов вредных влияний. Влияние таких факторов,
как изменение атмосферного давления, простыми средствами не
устранить. В тех случаях, когда соблюдение определенных требований
является обязательным. приходится применять барокамеры с
регулируемым давлением. Обычно в этих камерах можно одновременно
регулировать влажность и температуру.
2. Исключение систематических погрешностей в процессе измерения.
Исключению таким путем поддаются в основном инструментальные
погрешности, погрешности от установки и погрешности от внешних
влияний.
Характерным для рассматриваемых ниже способов устранения
погрешностей в процессе измерения является необходимость проведения
повторных измерений, поэтому они применимы в основном при
измерениях стабильных параметров и явлений.
Способ замещения заключается в том, что измеряемый объект
заменяют известной мерой, находящейся при этом в тех же условиях, в
каких находился он сам.
Пример: объект, электрическое сопротивление, индуктивность или
емкость которого требуется измерить, включают в измерительную цепь. В15
большинстве случаев при этом пользуются нулевыми методами
(мостовые, компенсационные и др.), при которых производится
электрическое уравновешивание цепи. После уравновешивания вместо
измеряемого объекта, не изменяя схемы, включают меру переменного
значения: магазин сопротивления, емкости, индуктивности, переменный
конденсатор или индуктивность. Изменяя их значение, добиваются
восстановления равновесия цепи. В этом случае способ замещения
позволяет исключить остаточную неуравновешенность мостовых цепей,
влияние на цепь магнитных и электрических полей, взаимные влияния
отдельных элементов цепи, а также утечек и других паразитных явлений.
Способ компенсации погрешности по знаку заключается в том, что
измерения следует проводить таким образом, чтобы погрешность в
результате измерений вошла один раз с одним знаком, другой раз – с
противоположным. Погрешность исключается при вычислении среднего
значения. Способ противопоставления заключается в том, что измерения
проводят два раза, причем так, чтобы причина, вызывающая погрешность,
при первом измерении оказала противоположное действие на результат
второго.
Способ введения поправок основан на знании систематической
погрешности и закономерности ее изменения. В этом случае в результат
измерения, содержащий систематические погрешности, или в показания
прибора вносят поправки, равные этим погрешностям, но с обратным
знаком.
\\\\\Дисперсионный анализ (критерий Фишера)
Способ последовательных разностей (критерий Аббе)\\\
18. Обработка результатов прямых однократных измерений
Результат прямого однократного измерения физической вели-
чины YИЗМ = А – это показание, снятое непосредственно с используе-
мого средства измерения.
Погрешность результата измерения включает погрешность
СИ, погрешность использованного метода измерения и субъективную
погрешность оператора. Каждая из этих составляющих может иметь
неисключенные систематические и случайные погрешности.
Оценивание погрешностей прямых однократных измерений
можно подразделить на точное и приближенное.
Рассмотрим методику точной оценки. Пусть число неисключен-
ных систематических погрешностей равно т и каждая задана грани-
цами ±θi , или доверительными границами ±θi(Рj), т.е. границами с из-вестной доверительной вероятностью Рj = РДj. В этом случае довери-тельная граница систематической составляющей результата изме-рения θ = θ(PД) оценивается с задаваемой доверительной вероятно-стью Рд по одной из следующих формул:
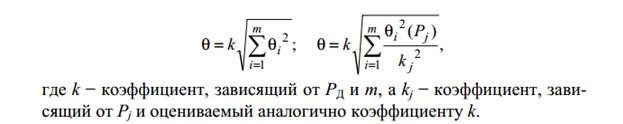
Большую часть измерений, проводимых при проверке, настройке и регулировке различных радиоэлектронных устройств, составляют обыкновенные однократные (технические) прямые измерения. Особенность таких измерений состоит в том, что, поскольку измерение выполняется без повторных наблюдений, по данным эксперимента нельзя отделить случайные погрешности от неисключенных систематических. Поэтому для погрешности результата измерения, как правило, оценивают только ее границы. Оценка границ погрешности результата таких измерений осуществляется на основе нормативных данных о свойствах используемых СИ (на основе метрологических характеристик СИ, приводимых в техническом описании). Поскольку нормы относятся к любым экземплярам СИ определенного типа, у конкретного экземпляра, используемого в конкретном измерении, действительные свойства могут отличаться от их норм. Но погрешности исправного СИ, используемого в конкретном измерительном эксперименте, никогда не могут превышать норм, указанных в нормативно технических документах на СИ данного типа!
Для высокоточных СИ и средств измерений, используемых в качестве образцовых, систематическая и случайная составляющие погрешности могут нормироваться отдельно. Для большинства СИ, предназначенных для технических измерений, нормируется предел допускаемого значения суммы систематической и случайной погрешностей. На основе этой метрологической характеристики устанавливаются классы точности СИ. Класс точности - обобщенная характеристика точности СИ. В соответствии с ГОСТ 8.401-80 "ГСИ. Классы точности средств измерений. Общие требования", классы точности устанавливаются для СИ, у которых погрешность нормируется в виде пределов допускаемой основной и дополнительных погрешностей. Предел допускаемой основной погрешности нормируется для нормальных условий эксплуатации СИ, которые особо оговариваются в техническом описании. Если рабочие условия эксплуатации СИ отличаются от нормальных - возникают дополнительные погрешности. Пределы допускаемых дополнительных погрешностей нормируются по отдельности для каждого влияющего фактора, выражаются, как правило, в виде дольного значения предела допускаемой основной погрешности и также приводятся в техническом описании (паспорте) СИ.
Классы точности присваиваются СИ при их разработке по результатам метрологической аттестации и подтверждаются (или не подтверждаются) при периодических поверках СИ в процессе эксплуатации. Основные правила нормирования погрешностей СИ в соответствии с ГОСТ 8.009-84 можно сформулировать следующим образом:
нормировать следует все свойства СИ, влияющие на точность результатов измерений;
каждое из подлежащих нормированию свойств следует нормировать по отдельности;
способы нормирования должны давать возможность экспериментально проверить соответствие каждого экземпляра СИ установленным нормам и притом так, чтобы указанная проверка была возможно более простой;
нормирование должно быть выполнено так, чтобы по установленным нормам можно было выбирать СИ и оценивать погрешности результатов измерений.
19. Обработка результатов прямых многократных измерений
Прямое многократное измерение
Необходимость многократных наблюдений некоторой физиче-
ской величины возникает при наличии в процессе измерений значи-
тельных случайных погрешностей. В этом случае задача состоит в
том, чтобы по результатам наблюдений найти оценку истинного зна-
чения и интервал, в котором находится сама величина с заданной ве-
роятностью. Решение задачи достигается способом статистической
обработки результатов наблюдений, основанном на гипотезе о рас-
пределении случайных погрешностей этих результатов по известному
закону.
Многократные измерения позволяют уменьшить (отфильтро-
вать) случайную погрешность. Для исключения погрешности необ-
ходимо бесконечное количество измерений. При ограниченном
числе измерений находится лишь оценка случайной погрешности.
Оценки – это случайные величины (в отличие от моментов), кото-
рые должны удовлетворять условиям состоятельности, несмещен-
ности, эффективности.
Краткая методика обработки результатов
многократных измерений
Предполагается, что наблюдения выполняются одним экспери-
ментатором в одинаковых условиях, одним и тем же прибором.
1. Проводят N единичных измерений Y’1...Y’N.
2. Исключают известные систематические погрешности из ре-
зультатов и получают исправленные значения Y1...YN.
3. Находят среднеарифметическое и принимают его за результат
измерений (Ycp).
4. Вычисляют оценку среднеквадратического отклонения ре-
зультатов:
а) определяют σ* (точность метода при единичном измере-
нии);
б) находят относительное значение среднеквадратической по-
грешности отн cp
σ = σ * * / Y ( точность метода при единичном измере-
нии).
5. Вычисляют оценку среднеквадратического отклонения ре-
зультатов измерений σ = σ
ср.отн отн
* * / N (это погрешность результата
после обработки многократных измерений).
6. Проверяют гипотезу о том, что распределение результатов
наблюдений нормальное (например построением гистограммы).
7. Вычисляют доверительные границы случайной погрешности:
а) их задают доверительной вероятностью, учитывая объем
выборки N;
б) вычисляют доверительные границы для данного закона
распределения.
20. Обработка результатов косвенных измерений
Погрешности косвенных измерений
Особенность косвенных измерений состоит в том, что величина
А, значение которой надо измерить, является известной функцией ƒ
ряда других величин – аргументов х1, х2, …, хm. Данные аргументы
подвергаются прямым измерениям, а величина А вычисляется по
формуле A = ƒ(х1, х2, …, хm).
Таким образом, при косвенных измерениях искомое значение
находится на основании известной функциональной зависимости по
результатам прямых измерений. Определение погрешности базирует-
ся на двух теоремах.
http://www.studfiles.ru/dir/cat34/subj197/file14760/view149316.html
http://e.lib.vlsu.ru/bitstream/123456789/1104/1/940.pdf
