Свойства операций над множествами

Глава I Множества. Логика

Множества

Грядущие поколения будут
рассматривать теорию множеств
как болезнь, от которой они излечились.

А. Пуанкаре, 1908 год

Определение 1. “Множество – совокупность элементов, обладающих определенными свойствами и связанных между собой или элементами других множеств определёнными отношениями ” (Н. Бурбаки).

Замечание.Подчёркнутые слова не определяются.

Замечание. “Множество есть многое, мыслимое как единое целое” (Г. Кантор – основатель теории множеств).

Определение 2. Задать множество – указать точное правило, с помощью которого о любом элементе можно сказать: является ли он элементом данного множества. Это можно сделать перечислением (для конечных множеств) или указанием характеристического свойства 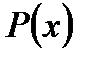, т.е. такого свойства, которым обладают все элементы задаваемого множества и не обладают никакие элементы никаких других множеств. Обычно множество выделяется из более общего множества, которое называется UNIVERSUM (вселенная) и обозначается буквой U.

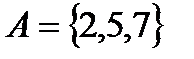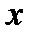Пример. Множество – множество, заданное перечислением; множество – множество элементов , заданное правилом 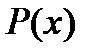. Например, – множество тех, и только тех действительных 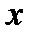, которые не больше двух.

На универсуме Uмножества обозначаются кругами, которые называются кругами Эйлера. Множества обозначаются большими буквами латинского алфавита, элементы – соответствующими маленькими (рис.1).

Рис.1Hhhfghfutu6uu1111111111111111111

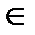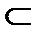Знак означает принадлежность и применяется для элементов, – не принадлежать, – принадлежать для множеств. Множество, не содержащее ни одного элемента, называется пустым и обозначается .

Определение 3.Два множества называются равными, если они состоят из одних и тех же элементов. Обозначается .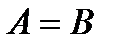

Пример. ; но , так как единственным элементом множества является упорядоченная пара , а множество состоит из двух элементов: 1 и 2.

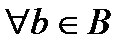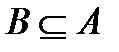Определение 4. Множество есть подмножество множества , если справедливо . Обозначается: . Говорят, что множество строго включено во множество , если справедливо, что , но .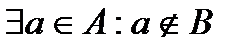

Определение 5. 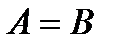, есл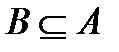и и (т.е. они состоят из одних и тех же элементов).

Пример. , так как единственным элементом множества является множество .

Определение 6.Рассмотрим множество всех подмножеств конечного множества и обозначим его . Таким образом, содержит пустое множество и само множество . Эти подмножества называются несобственными, а остальные собственными (собственно говоря, они и есть нетривиальные подмножества).

Пример.Пусть 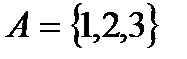, тогда .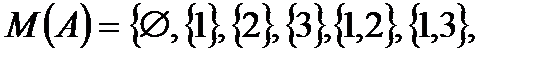

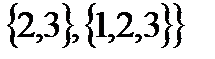Рис. 2

Определение 7. Объединением множеств и ( (читается чашка ) называется новое множество , элементами которого являются элементы множества или элементы множества : (рис.2). Слово “или” употребляется в неразделительном смысле и обозначается значком , который называется “дизъюнкция” (от лат. disjunctio – разобщение, различие). Тогда .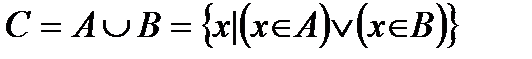

Аналогично даются определения остальных операций над множествами. Мы их просто выпишем.

Определение

Рис. 3

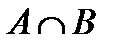8. Пересечение: (читается крышка ).

(рис.3). Слово “и” обычно заменяют значком - “конъюнкция” (от лат. conjunctio – союз, связь), и тогда множество описывается так: .

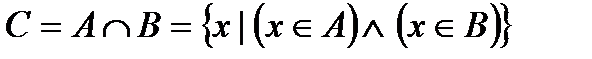Рис. 4

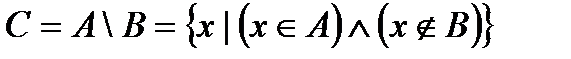Определение 9. Разность: (рис. 4) - все те элементы множества , которые не являются элементами множества .

Рис. 5

Определение 10. Симметрическая разность (дизъюнктивная сумма):

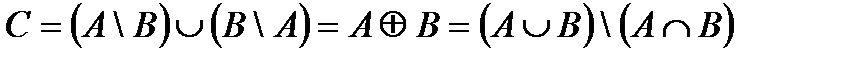(рис.5).

Рис.6

Определение 11. Дополнением множества до универсума называется множество, состоящее из всех тех элементов универсума, которые не являются элементами множества (рис. 6). Обозначают .

Определение 12. Характеристической функцией множества называется функция .

Легко составить характеристические функции для всех перечисленных операций. Они называются таблицами Буля. С их помощью легко доказываются свойства операций над множествами.

U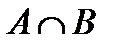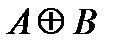

Свойства операций над множествами

– коммутативность;

– ассоциативность;

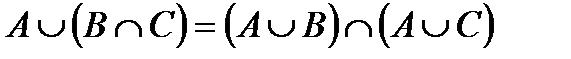– дистрибутивность;

– идемпотентность;

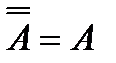– двойное отрицание;

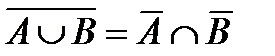– закон Моргана;

7. 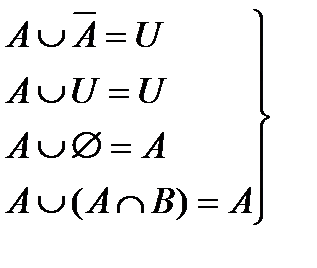- законы поглощения.

Определение 13.Символы и , Uи называются двойственными. Методом таблиц Буля легко показать, что имеет место принцип двойственности: при замене в любом свойстве входящих в него символов на двойственные, оно остается верным.

Пример. Докажем, например, закон Моргана.

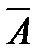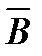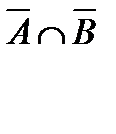Отношения

В мире всё относительно

и, прежде всего, отношения.

Абу Али аль-Хавои.

Определение 1. Два элемента одного или разных множеств, расположенные в определенном порядке, называется упорядоченной парой .

Определение 2. Две упорядоченные пары и 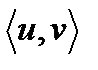равны, если .

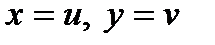Замечание.Естественно, , если .

Замечание.Упорядоченная n-ка (читается энка): .

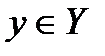Определение 3. Декартовым (прямым) произведением множеств и (обозначается ) называется множество всех упорядоченных пар таких, что , а . Множество часто называют множеством прообразов, а множество – множеством образов.

Определение 4.Любое подмножество декартова произведения называется бинарным отношением между множеством и (обозначается ).

Среди бинарных отношений важнейшим является функция (от лат. functio– исполнение).

Определение 5.Пусть 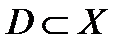, а .Подмножество декартова произведения множеств называется функцией, если есть парный элемент точно одной пары . Обозначается .

Определение 5^*.Если 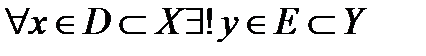, то такое отношение и его результат называется функцией. Множество называется областью определения функции, а множество – областью измененияфункции; 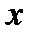называют аргументом (от лат. functio - действовать), 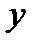– значением функции.

Определение 6.Функция называется инъективной, если 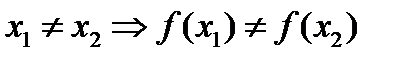, то есть каждому 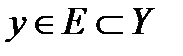соответствует не более одного .

Определение 7. Функция называется сюръективной, если , то есть каждому соответствует, по крайней мере, один .

Определение 8.Функция называется биективной, если она и инъективна и сюръективна, т.е. . Так как в этом случае каждому соответствует единственный , то существует функция , которая называется обратной по отношению к функции ( – обозначение обратной функции).

Элементы логики

"Всё наше достоинство заключено в мысли".

Б. Паскаль.

"Но если не грешить против разума, нельзя

вообще ни к чему прийти".

А. Эйнштейн.

Н. Бурбаки начинает свою книгу «Начала математики» так: «Со времён греков говорить «математика» значит говорить «доказательство»». В этом пункте мы обсудим, что такое доказательство.

Высказывания

Определение 1. Высказыванием называется любое верифицируемое повествовательное предложение, т.е. предложение, относительно которого можно утверждать истинно оно или ложно.

Пример« » – высказывание; «сегодня хорошая погода» – не высказывание (для кого как!).

Определение 2.Предложение, содержащее переменную и обращающееся в высказывание при подстановке конкретных значений называют высказывательной формой.

Пример.

Определение 3.Множество всех возможных истинных интерпретаций высказывания называется смысловым полем (интерпретация – это форма представления информации).

Смысловое поле задано на своём универсуме –множестве всех возможных интерпретаций. Это позволяет высказывания, как и множества, изображать кругами Эйлера. В этом случае характеристическая функция для высказываний имеет вид:

.

A –высказывание, а – его интерпретация.

Определение 4. Сложным называется высказывание, составленное из простых с помощью логических операций:ù – неверно, что; – конъюнкция; – дизъюнкция; – импликация; – эквивалентность; и кванторов: – существует, – для всех, - тавтология (всегда истинно).

Опишем эти операции, используя понятие смыслового поля:

или ù А – неверно, что А;

–дизъюнкция («или»), совокупность (disjunctio – различие);

–конъюнкция («и»), система (conjunctio – союз);

–импликация, теорема (implictio – тесно связывать);

– эквивалентность (или ).

Это описание позволяет составить таблицы истинности для этих операций.

A	B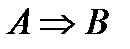
и	и	л	и	и	и	и
и	л	л	и	л	л	л
л	и	и	и	л	и	л
л	л	и	л	л	и	и

Теперь можно точно дать определения.

Определение 5 Дизъюнкцией двух высказываний и называется новое сложное высказывание , которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний или .

Определение 6. Конъюнкцией двух высказываний … (самостоятельно)

Определение 7. Эквиваленцией … (самостоятельно).

Определение 8. Импликацией двух высказываний и называется новое сложное высказывание , которое ложно тогда и только тогда, когда высказывание истинно, а высказывание ложно.

Импликация называется ещё теоремой. Тогда говорят, что достаточное условие для , – необходимое условие для . Теорема называется прямой, 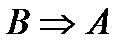– обратной, 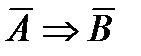– противоположная прямой, – противоположная обратной. Используя таблицы истинности, докажем три важных факта:

Теорема 1.Теорема эквивалентна теореме .

Теорема 2.Теорема 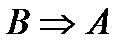эквивалентна .

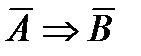Теорема 3.Теорема эквивалентна дизъюнкции .

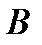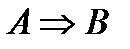и	и	и	л	л	и	и	и	и
и	л	л	л	и	и	и	л	л
л	и	и	и	л	л	л	и	и
л	л	и	и	и	и	и	и	и

■

Теоремы 1 и 2 называют законом контрапозиции, а теорему 3 – дизъюнктивной формой импликации.

Законы логики

Логикой называется наука о способах представления результатов мышления, способах доказательных рассуждений. Любое рассуждение состоит из высказываний. Истинность сложного высказывания, вообще говоря, зависит от истинности элементарных высказываний. Но существует такие сложные высказывания, которые истинны всегда, вне зависимости от истинности элементарных высказываний. Они называются законами логики. Рассмотрим некоторые из них.

I группа –законы, которые нельзя доказать, пользуясь таблицами истинности.

Закон тождества = (или ). Предмет рассмотрения не должен меняться в ходе рассмотрения.

Пример.2 и 3 числа. Числа бывают чётные и нечётные. 2 – чётное, 3 –нечётное. Но 2 и 3 есть 5. Следовательно 5 и чётно и нечётно одновременно. (изменился смысл «и»)

Закон достаточного основания. Любое высказывание должно быть достаточно обосновано. Этот закон запрещает ссылки при доказательстве на личное мнение, авторитеты, божественное откровение и пр.

Закон построения отрицания. ù ~ ù . Неверно, что для любого выполняется условие , эквивалентно тому, что существует такой , что условие для него не выполняется. Правило построения отрицания для предложений, начинающихся с кванторов заключается в следующем: квантор заменяется на , квантор заменяется на , знак отрицания переносится на предложение, стоящее за всеми кванторами.

II группа –законы, которые доказываются, используя таблицы истинности. Их формулировка всегда начинается со значка –«тавтология», т.е. «всегда истинно».

Перечислим некоторые из них:

1. Закон исключённого третьего:

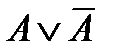
2. Закон исключения противоречий: ù .

3.Закон двойного отрицания: ù ù .

4. Закон Моргана: ~ .

5. Дизъюнктивная форма импликации: ~ .

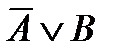6. Закон отрицания импликации: ~ .

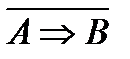7. Закон транзитивности: .

8. Закон контрапозиции: ~ .

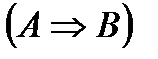9. Закон отрицания эквивалентности: ù ~ .

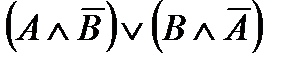10. Закон образования лжи: .

Методы доказательств

Определение 9.Та мысль, для обоснования истинности или ложности которой строится доказательство, называется тезисом. Тезис доказывается, исходя из некоторого основания с помощью доводов, связанных между собой и тезисом некоторой логической связью.

Поэтому любое доказательство можно представить в виде логической цепочки . Ошибки в доказательствах бывают в основном 5 типов:

1. ошибочен тезис;

2. ошибочно основание;

3. ошибочны доводы;

4. логическое самопересечение цепочки рассуждений:

;

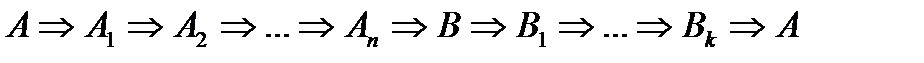5. некорректное использование законов логики (правил вывода).

Чтобы избежать ошибки в тезисе, надо чётко уяснить себе, что же именно доказывается, и помнить о законе тождества. Ошибки в основании и доводах – это или ложное, или произвольное основание (довод). Для избежания ошибок типа логического самопересечения (от лат. circulus vitiosus – порочный круг) математика имеет строго иерархическую структуру, о которой поговорим позже. Нас сейчас интересует корректные методы рассуждений. Перечислим некоторые из них.

1. Modus ponens (подтверждающая форма): .

Читается: истинно, что из следует ; имеет место . Следовательно, имеет место .

Пример.«Если у человека температура, то он болен. У человека температура. Следовательно, он болен». (Это не означает, что если температуры нет, то человек здоров.)

Определение 10.В этом случае говорят, что есть достаточное условие или достаточное, но не необходимое условие (как в нашем примере). называется признаком .

2. Modus tollens (отрицающая форма) - закон контрапозиции: .

Читается: из следует ; имеет место 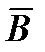. Следовательно, имеет место .

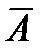Пример.«Если у человека высокая температура, он болен. Человек здоров. Следовательно, у него нет температуры». Если не выполняется, то не выполняется и (необходимое условие). Но если выполняется , это не значит, что выполняется . (Если человек болен, это не значит, что у него есть температура). В этом случае говорят, что есть необходимое, но не достаточное условие .

3. Закон эквивалентности :.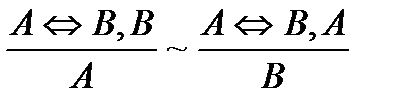

В этом случае говорят, что есть необходимоеидостаточное условие («если и только если») или есть критерий .

4. Логическая транзитивность: .

Наиболее часто встречаются ошибки при использовании этого правила. Главная из них – нечёткое определение объекта транзитивности.

Пример.Учитель считает, что учится лучше , если в большинстве контрольных работ оценка у выше, чем у . При этом определении термина «лучше» легко привести пример, когда будет лучше , будет лучше , а лучше, чем .

	К1	К2	К3
А
В
С

5. Reductio ad absurdum (закон образования лжи) - доказательство от противного:

Одна из форм:

В этом случае говорят, что если из 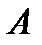следует и , и не , то 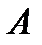- ложь.

Ещё одна форма: требуется доказать, что из следует .

Пусть имеет место , но не имеет место . Применяя закон логической транзитивности, строим цепочку , т.е. из . Следовательно, по закону контрапозиции . Если в доказательстве используется одна из форм образования лжи, то перед началом ставится значок (ad absurdum). Пример применения этого закона будет ниже.

6. Метод математической индукции. Применяется для высказываний, зависящих от натурального параметра . Докажем следующую теорему:

Теорема 4.Утверждение 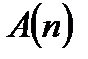справедливо 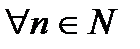, если:

1. 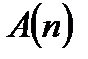справедливо при ;

2. из справедливости для произвольного следует справедливость его для .

. Пусть утверждения 1 и 2 выполняются, но справедливо не для всех . Так как, справедливо при (утверждение 1), то существует такое , где , при котором не справедливо, причём ещё справедливо. Положив 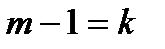, мы получим противоречие с утверждением 2. ■

Для применения метода математической индукции следует сделать следующие операции:

1. Ставится «математический эксперимент», и получают .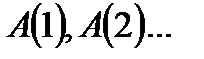

2. Делается предположение о виде формулы .

3. Проверяется утверждение 1 (фактически на первом этапе).

4. Доказывается утверждение 2.

Пример.Помимо утверждений, связанных с натуральными числами, методом математической индукции хорошо доказывать неравенства, признаками делимости и т.д.

Докажем, например, методом математической индукции, что , .

1. При имеем .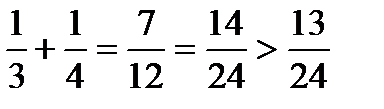

2. 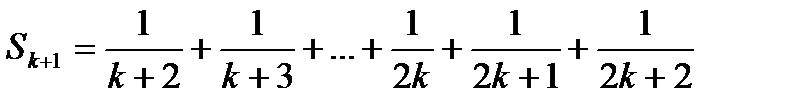, тогда

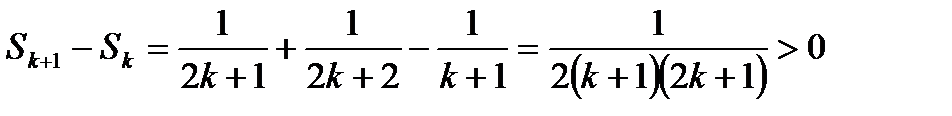, а т.к. и , то . ■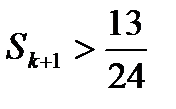

7.В предыдущем примере применён ещё один приём, который называют метод «расчленения»: если 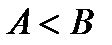, , то . Этот частный случай логической транзитивности, где промежуточное значение чётко определено.

Пример.Теорема Смоллиана о вечном блаженстве: «Что может быть лучше вечного блаженства? Ничего. А корка сухого чёрного хлеба лучше, чем ничего».

Здесь приведены далеко не все приёмы рассуждений, а лишь те, которые мы будем использовать достаточно часто.

Аксиоматический метод

1. Любое доказательство начинается с основания (посылки). Но основание не должно быть ложным, т.е. его тоже нужно обосновать. По сути дела, доказательство – это дедукция, т.е. переход от более общих утверждений к частным. Доказать – значит установить, что данное утверждение есть следствие более общего, т.е. выводится из него.

2. Самые общие утверждения в математике называют аксиомами (от греч. axios– ценность). Аксиомы – это не положения, истинность которых очевидна (сколько угодно теорем, истинность которых очевидна, доказывается), а просто утверждения, которые удобно из методических или методологических соображений принять за исходные.

3. Аксиоматическое построение теории осуществляется по следующей схеме:

1) перечисляются исходные понятия, которые вводятся без определений;

2) формулируются исходные предложения, выражающие основные свойства и отношения между исходными понятиями, аксиомы и определения.

3) На основе аксиом и определений формулируются остальные предложения теории - теоремы (от греч. teos– божественный). При этом можно использовать ранее доказанные теоремы.

4) Любая теорема должна обладать свойством выводимости (разрешимости), т.е. должен существовать способ получения её из данной системы аксиом.

5) Система аксиом должна быть полной, непротиворечивой, независимой.

Полнотаозначает, что система аксиом имеет единственную с точностью до интерпретации реализацию, т.е. не существует истинных утверждений, которые нельзя доказать, опираясь на эту систему аксиом. Непротиворечивость означает, что из данной системы аксиом нельзя сделать двух взаимоисключающих друг друга выводов. Другими словами, как бы мы не развивали теорию, базирующуюся на этой аксиоматике, мы не получим противоречий. Независимость означает, что ни одну из аксиом системы нельзя доказать, как теорему, базируясь на остальных. (Это последнее требование, вообще говоря, неважно, т.к. увеличение числа аксиом облегчает построение теории).

Давид Гильберт поставил задачу доказательства непротиворечивости всей математики, «исключив из неё всякого рода метафизику». Исследование программы Гильберта обоснования математики показало, что непротиворечивость любого её раздела можно связать с непротиворечивостью арифметики. Но в 1931 году Курт Гёдель доказал две теоремы.

Теорема 5. Если формально-логическая система, содержащая арифметику, включая и саму арифметику, непротиворечива, то она неполна, т.е. существуют утверждения, сформированные в её исходных понятиях, которые нельзя доказать или опровергнуть.

Теорема 6. Если формально-логическая система, содержащая арифметику, включая и саму арифметику, непротиворечива, то это нельзя доказать средствами и языком любой математической теории, содержащей арифметику.

Таким образом, математику невозможно самообосновать. Её обоснование – в природе человека и в его культуре.