Определение 1. Пусть и произвольные множества. Соответствием называется тройка множеств 5 страница

Теорема 7. Транзитивным замыканием толерантности является эквивалентность.

Доказательство. Пусть отношение толерантности, заданное на множестве . Тогда и по теореме 7 отношение рефлексивно и транзитивно. Осталось доказать, что оно еще и симметрично.

Поскольку отношение симметрично, то оно удовлетворяет условию леммы 2, по которой также рефлексивным и симметричным будет и отношение , и, следовательно, к нему также применима лемма 2. Поэтому отношение 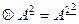также рефлексивно и симметрично. На том же основании симметричным и транзитивным будет отношени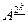е , где 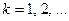. 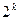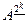Но как только станет больше длины кратчайшего пути между самыми удаленными вершинами графа отношения , так отношение станет равным отношению 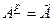. Но раз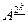 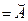, а отношение 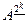симметрично, тогда симметрично и отношение . Таким образом, отношение эквивалентность, что и требовалось доказать.

Вопросы для самоконтроля

3. При каких операциях над рефлексивными отношениями сохраняется свойство рефлексивности?

4. При каких операциях над симметричными отношениями сохраняется свойство симметричности?

5. Определите классы толерантности в отношении «приблизительно равны с ошибкой не более 1», заданном на множестве .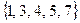

Отношения порядка

Определение 18. Строгим порядком называют отношения, которые одновременно антирефлексивны и транзитивны, т.е.

( строгий порядок )

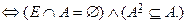
Например, отношение «меньше» антирефлексивно, т.к. условие 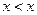не выполняется ни при каком значении , и транзитивно (условие 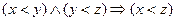выполняется при любых значениях 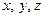), следовательно, это строгий порядок. Другие примеры отношений строгого порядка: «больше», «старше», «сильнее», «правее», «ниже», «быть предком», «быть потомком» и т.д.

Отношение «быть меньше ровно на единицу» строгим порядком не является, т.к. оно не транзитивно, но его транзитивное замыкание (отношение «меньше») есть строгий порядок.

Теорема 8. Отношение строгого порядка асимметрично, т.е.

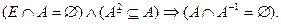
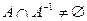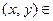
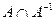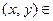
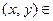
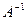Доказательство. Предположим противное. Пусть . Тогда существует пара . Откуда и или 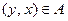, т.е. выполняется условие 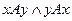, из которого на основании свойства транзитивности следует выполнение условия 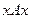, т.е. 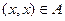, но это противоречит свойству антирефлексивности отношения . Данное противоречие и доказывает, что 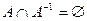. Теорема доказана.

Определение 19. Нестрогим порядком называют отношения, которые одновременно рефлексивны, антисимметричны и транзитивны, т.е.

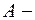нестрогий порядок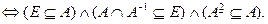

Примеры отношений нестрогого порядка: «меньше либо равно» ( 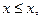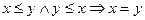, 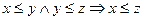для любых 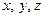), «не меньше», «не выше», «не хуже», «быть подмножеством» ( 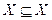, , 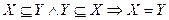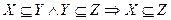для любых множеств ).

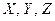Множество , на котором задано отношение порядка (строгого или нестрогого), называется полностью упорядоченным, если для любых отличных друг от друга элементов и этого множества будет выполняться либо условие 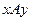, либо условие .

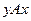Примерами полностью упорядоченных множеств являются все числовые множества, т.к. любые два различных числа можно сравнить и определить наибольшее (наименьшее).

Определение 20.Множество называется частично упорядоченным, если на нем задано отношение порядка (строгого или нестрогого), но не для любых его элементов и выполняется условие 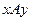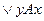, а само это отношение называется частичным (строгим или нестрогим) порядком.

Например, отношение «быть подмножеством», является частичным нестрогим порядком, а совокупность множеств, на которой он задан, будет частично упорядоченным множеством. В этой совокупности не любые множества сравнимы между собой. В частности, отрезок 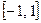действительной оси не сравним с отрезком 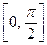(отрезок 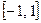не является подмножеством отрезк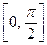а , а 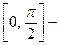подмножеством 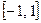, что означает их несравнимость).

Примером частичного порядка является также отношение «подчиненности», определенное на множестве сотрудников некоторого учреждения (директору подчиняется начальник отдела, но начальники разных отделов друг другу не подчиняются).

Отношения порядка (а к ним относится еще и не рассмотренный здесь древесный порядок [7]) не менее эквивалентности важны в научных исследованиях. Все наши знания, да и вся человеческая деятельность, по крайней мере частично упорядочены. Такова природа процесса познания реального мира. Процесс познания мира математики задается отношением «определяться через более широкое понятие». В частности, изложение материала в настоящем пособии идет в соответствии с тем порядком, который задается данным отношением. Отталкиваясь от понятия абстрактного множества, мы дали четкие математические определения подмножеству, разбиению, соответствию, логической функции, отношению и многим другим математическим объектам (эйдосам). Такая последовательность изложения продиктована самой природой мира математики, который, как теперь выяснилось, является упорядоченным множеством математических понятий.

Вопросы для самоконтроля

1. Докажите, что противоположным отношению строгого порядка будет нестрогий порядок.

2. На множестве всех определенных выше математических объектов задано отношение «определяется через». Задайте данное отношение в виде графа.

5.2. Булевы функции

Особое место в математике занимают логические функции, аргументами которых являются двузначные логические переменные, т.е. в самом общем виде эти функции суть однозначное соответствие вида

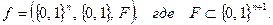(5.18)

Здесь число независимых переменных, от которых зависит функция 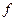( 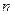=1, 2, …); 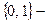область изменения этих переменных (такие переменные называют булевыми), а также и область значений 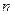-арной булевой функции 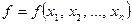, график которой определяется множеством , представляющим собой 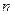-мерную «гиперкривую» в гиперплоскости .

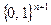В технике существует эквивалентное название – переключательные функции (ПФ). Данное название указывает на то, что переключательные функции реализуются схемами с использованием вентильных элементов (т.е. логических элементов, представляющие собой схемы переключения электрических сигналов).

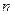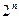Обратим внимание, что областью отправления соответствия (5.18) является единичный -мерный гиперкуб. Гиперкуб - это множество из элементов, а булеан гиперкуба (множество всех его подмножеств) будет содержать уже 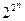элементов. Согласно (5.18) любая булева функция определяет разбиение гиперкуба на две области (истинности и ложности). Поэтому число различных функций 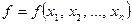равно 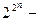числу различных подмножеств гиперкуба .

Поскольку области значений таких функций и их переменных полностью совпадают, то это дает возможность в качестве аргумента булевой функции использовать булеву функцию и тем самым получить новую булеву функцию. Иначе говоря, на множестве булевых функций задана операция композиции 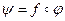, позволяющая из функци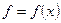й и 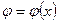сконструировать еще одну булеву функцию .

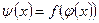Следовательно, на множестве булевых функций можно найти минимальный набор самых простейших (изначальных) функций, из которых, с помощью применения операции композиции произвольное число раз, можно будет получить все остальные булевы функции. Видимо и в мире булевых функций существует неравнозначность, удерживаемая некоторым порядком, который нам предстоит открыть. Этим и займемся.

5.2.1. Логические операции соединения

Сначала рассмотрим множество бинарных булевых функций, т.е. функций 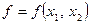двух ( 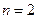) булевых переменных и . Бинарные булевы функции еще называют логическими операциями соединения. Их общее число равно 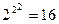. Столько подмножеств имеет единичный квадрат 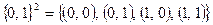, изображенный на рис. 5.7 и 5.8.

Полный перечень бинарных булевых функций представлен в табл. 5.1.

В данной таблице в крайнем левом столбце указаны булевы переменные ( и ) и функции ( , , …, 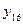) как обозначение соответствующих строк таблицы. В последующих четырех столбцах указаны области истинности соответствующих функций. В первой строке этих столбцов указаны номера вершин единичного квадрата (рис. 5.7), а во второй и третьей строках – координаты этих вершин (первая и вторая компоненты соответственно).

В строках, помеченных символами , , …, , 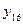в области этих столбцов стоят нули и единицы. Единицы указывают, какие вершины единичного квадрата принадлежат области истинности соответствующей функции 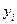. Поскольку строка содержит одни нули, то область истинности данной функции (константы «ложь») – пустое множество. В строке только одна единица, соответствующая вершине 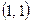с номером 3 единичного квадрата 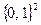, и, следовательно, областью истинности для конъюнкции будет подмножество .

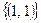Таблица 5.1

					Название функции	Обозначение
					константа «ложь»
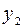					конъюнкция (логическое умножение)
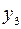					запрет ( запрещает )
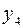					пустая операция над
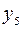					запрет ( запрещает )
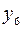					пустая операция над
					сложение по модулю 2
					дизъюнкция (логическое сложение)
					стрелка Пирса
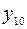					эквиваленция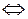
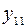					инверсия (отрицание )
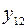					импликация ( влечет )
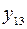					инверсия (отрицание )
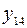					импликация ( влечет )
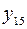					штрих Шеффера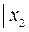
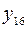					константа «истина»

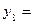
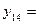
1 3 1 3