Глава третья. суждение, вопрос, норма.

	1. Что представляет собой такая форма мышления как суждение?

Суждение представляет собой форму мышления, в которой закрепляются полученные человеком знания об отдельных предметах или их классах, тех или иных событиях, ситуациях и т.п..

Суждение– это форма мышления, в которой что-либо утверждается или отрицается о предметах действительности, об их свойствах или отношениях.

Например: «Некоторые столицы расположены в Европе» или «Если у меня будет свободное время, то я обязательно схожу на каток» и т.п.

Характерной особенностью суждения является то, что оно – при логически правильном его построении – может быть истинным или ложным. Напомним, что суждение считается истинным, когда его содержание соответствует действительности. Суждение считается ложным, когда оно не соответствует реальному положению вещей. В обыденном языке суждение имеет, как правило, форму повествовательного предложения. Само суждение при этом выражает смысл этой знаковой формы.

2. Какие элементы входят в состав суждения?

В структуре любого простого суждения выделяют субъект и предикат, которые называют терминами, а также связку.

Субъект суждения -этопонятие опредмете мысли. Т.е. то, о чем говорится в суждении.

Предикат суждения -понятие опризнаке предмета мысли, наличие которого утверждается или отрицается в суждении. Это то, что говорится о предмете мысли.

Связка суждения –это то, что связывает его субъект и предикат.

Связка суждения чаще всего выражается вспомогательными глаголами«есть» («не есть»), «суть» («не суть») и т.п. и характеризует его с качественной стороны.

Субъект суждения в традиционной логике обозначают символом S, а предикат - символомP, что дает возможность записать структуру простого суждения в виде выражения

S есть (не есть) P

В структуре простого суждения могут встречаться вспомогательные слова «некоторый», «все», «любой», «каждый», «ни один», «среди» и т. п. Эти слова называют кванторными словами. Они характеризуют суждение с его количественной стороны. Учитывая наличие в суждении кванторных слов, структуру простого суждения можно представить в виде следующих выражений: «Все S есть P», «Ни одно S не есть P», «Некоторые S есть/не есть P». Такую форму суждения нередко называют его четкой логической формой.

Например, суждение «Каждый следователь знает хотя бы одного адвоката» имеет форму «ВсеSестьP».

3. Какие виды простых суждений выделяют в логике?

Наиболее простыми и удобными для логического анализа являются так называемые простые категорические суждения, к которым относят все суждения, в которых говорится о свойствах субъекта. В случае необходимости логического анализа суждений иного вида, их по возможности преобразуют в удобную для этого форму категорического суждения, представляя его в четкой логической форме.

Все простые категорические суждения делят на виды в зависимости от количественной и качественной характеристики.

По своему качеству категорические суждения могут быть утвердительными или отрицательными. По количеству категорические суждения делятся на единичные, частные и общие.

		КАТЕГОРИЧЕСКИЕ СУЖДЕНИЯ

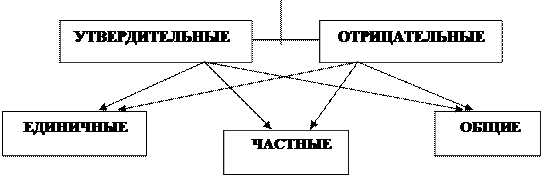Рис. 13

Утвердительное суждение –это суждение с утвердительной связкой «есть». Структура такого суждения (без учета количественной характеристики)имеет вид «S есть P».

Отрицательное суждение– это суждение с отрицательной связкой «не есть». Его структура (также без учета количественной характеристики): «S не есть P».

Примеры: «Лондон (S) является одной из столиц Европы (P)» - утвердительное суждение, «Некоторые суждения (S) не являются простыми (P)» – отрицательное суждение.

Единичное суждение– это суждение, субъектом которого является единичное понятие. Например: «Автор поэмы «Руслан и Людмила» – Александр Сергеевич Пушкин». Структуру единичного суждения можно представить как: «Данное S есть (не есть) P».

Общее суждение –это суждение, в котором речь идет обо всем объеме субъекта. Например: «Ни один лгун не является честным человеком». Структура общего суждения имеет вид «Все S есть (не есть) P».

Частное суждение– это суждение, в котором речь идет о некоторой части объема субъекта (а может быть и обо всем его объеме). Например: «Некоторые следователи не употребляют спиртного».Частное суждение имеет структуру «Некоторое S есть (не есть) P».

4.Что представляет собой объединенная классификация простых суждений?

В объединенной классификации простых суждений различают четыре вида суждений: общеутвердительное, общеотрицательное, частноутвердительное и частноотрицательное.

Единичное суждение в объединенной классификации относят к общим суждениям. Это связано с тем, что в единичных суждениях речь всегда идет обо всем объеме субъекта, объем которого представляет собой единичный класс.

	КАТЕГОРИЧЕСКОЕ СУЖДЕНИЕ

	общеотрицательное   НИ ОДНО S НЕ ЕСТЬ P		общеутвердительное   ВСЕ S ЕСТЬ P

Рис.14

Общеутвердительное суждение обозначают латинской буквой A, частноутвердительное - буквойI, общеотрицательное – буквой E, частноотрицательное – буквой O.

5.Можно ли выразить смысл простого суждения графически?

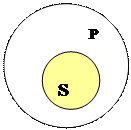
Смысл, а вместе с ним и истинность простого категорического суждения, тесно связаны с отношениями между его терминами. Каждому виду суждения соответствует та или иная графическая схема отношений между его терминами, при котором суждение считается истинным. Суждение типа A (Все Sесть P) является истинным при следующих отношениях между его терминами:

А) В)

Рис.15

Примером суждения, соответствующего схеме А), будет суждение «Любой равносторонний прямоугольник (S) является квадратом (P)». А примером суждения, соответствующего схеме Б) – суждение «Все школьники (S) – учащиеся (P)».

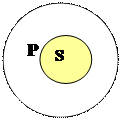
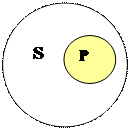
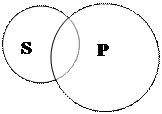
Суждение типаI (Некоторые S есть P) будет истинным, если отношения между его терминами соответствует таким схемам:

А) Б) В) Г)

Рис.16

Примеры: Для схемы А): «Некоторые квадраты(S) – равносторонние прямоугольники» (P);

Для схемы Б): «Некоторые деревья(S) являются растениями (P)»;

Для схемы В): «Некоторые растения(S) – деревья (P)»;

Для схемы Г): «Некоторые врачи (S) – женщины(P)».

Суждение типа O(Некоторые S не есть P) является истинным в случаях, когда отношения между его субъектом и предикатом соответствуют следующим графическим схемам:

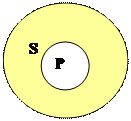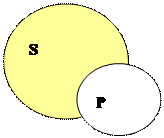А) Б) В)

Рис.17

Этим схемам соответствуют следующие суждения:

Для схемы А) – «Некоторые рабочие(S) не являются сталеварами(P)»;

Для схемы Б) – «Некоторые спортсмены(S) не являются студентами(P)»;

Для схемы В) – «Некоторые деревья(S) не являются грибами(P)».

Суждения типа E будут истинными при условии, что отношения между их терминами соответствуют такой графической схеме:

Рис.18

Примером такого рода суждений может быть суждение «Ни один полк (S) не является дивизией (P)».

6. Что выражает такая характеристика суждения как распределенность его терминов?

Распределенность того или иного термина в суждении связана с отношением терминов между собой.

Термин называется распределенным, если он рассматривается в этом суждении в полном объеме. Иначе говоря, термин распределен, когда он полностью включается в объем другого термина или полностью исключается из него.

В истинном общеутвердительном суждении субъект всегда распределен, а предикат может быть распределен или нераспределен. В истинном частноутвердительном суждении субъект в общем случае не распределен, то же самое можно сказать и о предикате этого суждения. В частноотрицательном суждении субъект также не распределен, а предикат во всех представленных случаях оказывается распределенным. Это видно на представленных выше графических схемах (рис. 15, 16, 17). Схема общеотрицательного суждения (рис. 18) ясно показывает, что в этом суждении оба термина распределены.

Итак, общий вывод, который можно сделать из анализа графических схем, следующий:

субъект всегда распределен в общих суждениях, а предикатвсегда распределен в отрицательных суждениях.

7. Какие виды сложных суждений различают в логике?

Сложное суждение образуется из простых суждений с помощью соединения их логическими союзами. Структура сложного суждения может быть записана с помощью языка логики высказываний.

Сложные суждения, в котором простые суждения связаны между собой союзом «и» или его аналогами («а», «зато», «да», «не только, но и …», как…, так и …», «но», «хотя и…, однако…» и т.д.) называются в логике соединительнымиили конъюнктивнымисуждениями. Например: «Квадрат – это и ромб, и прямоугольник». В языке логики высказываний это суждение можно записать как pÙq.

Сложные суждения, в которых используется разделительный союз «или» а также его аналоги (например, «то…, то…», «то ли …, то ли …», « не то …, не то …», «либо…, либо…» и т. п.) называют разделительнымиили дизъюнктивными.Они делятся на суждения, которые называют строго разделительными (строгой дизъюнкцией) и разделительно-соединительные (нестрогая дизъюнкция). В первом случае простые суждения, входящие в состав дизъюнкции исключают друг друга, во втором – нет. Примером строгой дизъюнкции может служить суждение «Храбрец или сидит в седле, иль тихо спит в сырой земле» (Р. Гамзатов). Примером нестрогой (слабой) дизъюнкции может быть суждение «Почтенный старец этот постоянно был сердит или выпивши (А. Герцен). В логике высказываний первое из суждений записывают как p Ú q , а второе – как p Ú q.

Сложное суждение, образованное с помощью логического союза «если…, то…» или его аналогов («раз…, то…», «как скоро…, то…», «потому, что…», «вследствие того, что…», «значит», «в связи с тем, что…», «для того, чтобы…», «когда», «лишь только…» и др.) называют условным(в логике его обозначают как p ® q). Например: «Как хорошо могли бы жить все люди на свете, если бы они только захотели…» (А. Фадеев).

С помощью условного суждения выражают причинные, целевые, временные, а также условные связи между предметами, событиями, явлениями, ситуациями, фактами и т.п. Нередко с помощью условного суждения формулируют высказывание, в котором одно из суждений рассматривается как обоснование другого.

Сложные высказывания, которые образуются с помощью логического союза «тогда и только тогда, когда…», которому в естественном языке соответствуют грамматические союзы, «если и только если…», «только и только если…» и др., называют суждениями эквиваленции. С помощью таких суждений выражают взаимную обусловленность событий, фактов, явлений, состояний, действий и т.п. Например: «Оценка письменной работы будет отличной, если и только если в ней не будет ни одной ошибки». Суждение эквиваленции с помощью символов логики высказываний можно представить в виде p º q.

Сложные высказывания, называемые отрицанием, образуются с помощью логических союзов «не» или «неверно, что». Если некоторое высказывание обозначить символомp, то его отрицание обозначается как ~р.

Отрицание в естественном языке может быть выражено различными способами: внешнее отрицание – с помощью словосочетания «неверно, что…», внутреннее отрицание – с помощью частиц «не» или «ни». Например: «Ни один человек, не достигший совершеннолетия, не может быть представителем в суде» или « Неверно, что данное суждение не является ни импликацией, ни эквиваленцией»).

8. От чего зависит значение истинности сложного высказывания?

Значение истинности сложных суждений зависит не только от истинности или ложности простых суждений, входящих в состав сложного суждения, но и от способа связи простых суждений между собой, т.е. от того или иного логического союза.

Так, суждение, называемое конъюнкцией (pÙq) считают истинным тогда и только тогда, когда истинны одновременно оба простых суждения, входящие в его состав.

Нестрогая дизъюнкция (p Ú q) - истинна в том и только том случае, когда истинно хотя бы одно из простых суждений его составляющих.

Строгая дизъюнкция (p Ú q) –считается истинной, если истинно одно и только одно из простых суждений, входящих в его состав.

Импликация (p ® q)- имеет значение «ложно» в том и только том случае, когда ее основание (суждение, выражающее условие) истинно, а следствие – ложно, в остальных случаях условное суждение считается истинным.

Суждение эквивалентности или равносильности (p º q) -истинно в том и только том случае, когда простые суждения, входящие в его состав имеют одно и то же значение истинности (одновременно истинны или одновременно ложны).

Сводная таблица истинности сложных суждений, состоящих из двух простых, может быть представлена следующим образом:

Pp	qq	p Ù q	p Ú q	p Ú q	p ®q	p º q
иИ	ИИ	И	И	Л	И	И
ИИ	ЛЛ	Л	И	И	Л	Л
ЛЛ	ИИ	Л	И	И	И	Л
ЛЛ	ЛЛ	Л	Л	Л	И	И

Таблица 1.

Суждение ~р, являющееся отрицаниемнекоторого исходного сужденияp, истинно в случае ложности этого исходного суждения и ложно, когда исходное суждение истинно. Таблица истинности этого высказывания такова:

~p	р~р
Ли	ил
Лл	ии

Таблица 2

9. Как установить значение истинности сложного высказывания, в котором более двух логических союзов?

Все значения истинности любого, как угодно сложного языкового выражения, состоящего из конечного и ограниченного числа простых суждений можно установить с помощью таблиц истинности. Для этого необходимозаписать это выражение на языке логики высказываний, а затем построить соответствующую этому выражению таблицу истинности, учитывая все возможные сочетания значений простых суждений.

Пусть нам необходимо установить значения истинности сложного суждения «Если я выполню домашнее задание сегодня, то у меня будет свободным выходной, и я смогу поехать за город». На языке логики высказываний его можно записать в виде формулы

p ® (q Ù r). Здесь три простых суждения, значит, в таблице будет восемь строк (количество строк таблицы истинности равно 2^{n ,} где n – число простых суждений, входящих в состав сложного высказывания).

Заполнив столбцы значений для суждений p,q, r, заполняем теперь столбец значений истинности для формулы p Ù q, после чего заполняем столбец для всей формулы, имея в виду, что это суждение - условное. В итоге таблица для этой формулы будет иметь следующий вид:

pp	qq	rr	q qÙr	p®( q Ù r)
ии	ии	ии	Ии	и
Ии	ии	лл	Ил	и
ии	лл	ии	ил	л
ии	лл	лл	лл	л
лл	ии	ии	ли	и
лл	Ии	лл	лл	и
лл	лл	Ии	лл	и
лл	ил	Лл	лл	и

Таблица 3

10. Какое высказывание называют в логике тождественно истинным или законом логики?

Сложное суждение, которое независимо от значения истинности простых суждений, входящих в его состав, всегда принимает значение «истинно» называют тождественно истинным суждением, тавтологией или законом логики. Формулу такого высказывания нередко называют общезначимой. Законами логики являются, например, выражения, структура которых соответствует формулам