Логические операции, их схемы и таблицы истинности.
Лекция №8
Понятие высказывания. Базовые логические операции, их схемы и таблицы истинности.
План
1. Понятие высказывания.
2. Логические операции, их схемы и таблицы истинности.
Понятие высказывания.
В 19 веке ирландский математик Джордж Буль создал алгебру логики и назвал Булевой алгеброй.
Логика – наука о законах мышления.
Булева алгебра является частью математической логики. Одно из применений Булевой алгебры – использование ее как алгебры высказываний или алгебры значений истинности.
Высказывание - это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Высказывания бывают простые и сложные. Сложные высказывания образуются из простых с помощью логических функций. Значение Булевой функции зависит от значения ее переменных. Наиболее наглядной формой задания таких функций является таблица истинности.
Таблица истинности — это таблица, описывающая логическую функцию.
Логические операции - мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логическое выражение - устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение - логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Логические операции, их схемы и таблицы истинности.
2.1 Логическое отрицание или инверсия (функция НЕ):
Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
F= 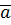
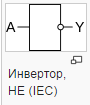 Таблица истинности для инверсии
Таблица истинности для инверсии
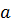 | F= 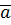 |
2.2 Логическое сложение или дизъюнкция (функция ИЛИ):
Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выражения ложны.
Обозначение: F = 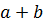 F =
F = 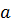 ˅
˅ 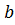 .
.
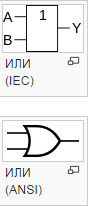 Таблица истинности для дизъюнкции
Таблица истинности для дизъюнкции
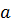 | 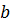 | F |
2.3 Логическое умножение или конъюнкция (функция И):
Конъюнкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = 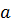 &
& 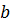 F =
F = 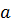 ·
· 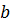 F =
F = 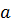 ˄
˄ 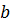 .
.
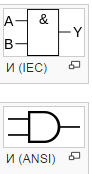 Таблица истинности для конъюнкции
Таблица истинности для конъюнкции
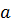 | 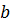 | F |
2.4 Логическое следование или импликация:
Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
F = 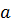 →
→ 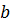
Таблица истинности для импликации
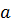 | 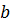 | F |
2.5 Логическая равнозначность или эквивалентность или тождество:
Эквивалентность - это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
F = 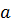 =
= 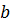 F =
F = 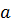 ↔
↔ 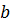 F =
F = 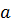 ~
~ 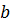 .
.
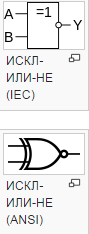 Таблица истинности для эквивалентности
Таблица истинности для эквивалентности
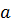 | 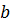 | F |
2.6Логическая неравнозначность или сложение по mod2 (функция исключающее ИЛИ):
Неравнозначностьюдвух высказываний 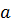 и
и 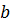 называют такое высказывание, которое истинно тогда и только тогда, когда одно из этих высказываний истинно, а другое ложно.
называют такое высказывание, которое истинно тогда и только тогда, когда одно из этих высказываний истинно, а другое ложно.
F = 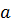

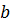 .
.
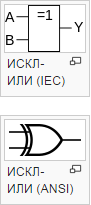 Таблица истинности для неравнозначности
Таблица истинности для неравнозначности
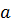 | 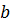 | F |
Операция исключающее ИЛИ фактически сравнивает на совпадение два двоичных разряда.
Логические операции инверсии, дизъюнкции, конъюнкции образуют полную систему логических операций, из которых можно построить сколь угодно сложное выражение. Порядок выполнения логических операций в сложном логическом выражении:
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Контрольные вопросы:
1. Кто создал алгебру логику?
2. Что такое высказывание?
3. Как образуются сложные высказывания?
4. Что такое таблица истинности?
5. Что такое логическое выражение?
6. Что такое инверсия и дизъюнкция?
7. Что такое неравнозначность двух высказываний?
8. Каков порядок выполнения логических операций в сложном логическом выражении?
Литература:
1. http://infolike.narod.ru/logic.html
2. Бочаров В.А., Маркин В.И. Основы логики.
