Логические операции над высказываниями

Краткие теоретические сведения

Под высказыванием обычно понимают всякое повество­вательное предложе-ние, утверждающее что-либо о чем-либо, и при этом можно сказать, истинно оно или ложно в данных условиях места и времени. Логически­ми значениями высказываний являются «истина» и «ложь».

Если высказывание а истинно, то а = 1, а если а ложно, то а = 0.

Логические операции над высказываниями

1. Отрицание. Отрицанием высказывания х называ­ется новое высказывание, которое является истинным, если высказывание х ложно, и ложным, если высказы­вание x истинно.

Отрицание высказывания х обозначается 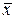и чита­ется «не х» или «неверно, что x».

Логические значения высказывания 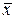можно опи­сать с помощью таблицы истинности

x

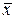2. Конъюнкция (логическое умножение). Конъюнк­цией двух высказываний х, у называется новое высказы­вание, которое считается истинным, если оба высказы­вания х, у истинны, и ложным, если хотя бы одно из них ложно.

Конъюнкция высказываний х, у обозначается сим­волом х&у или (х Ù у), читается «х и у». Высказывания х, у называются членами конъюнкции.

Логические значения конъюнкции описываются сле­дующей таблицей истин-ности:

x	y	х&у

3. Дизъюнкция (логическое сложение). Дизъюнкцией двух высказываний х, у называется новое высказывание, которое считается истинным, если хотя бы одно из выс­казываний х, у истинно, и ложным, если они оба ложны.

Дизъюнкция высказываний х, у обозначается сим­волом x Ú у, читается «х или у». Высказывания х, у называются членами дизъюнкции.

Логические значения дизъюнкции описываются сле­дующей таблицей истин-ности:

x	y	x Ú у

4. Импликация. Импликацией двух высказываний х, у называется новое выс-казывание, которое считается ложным, если х истинно, а у – ложно, и истинным во всех остальных случаях.

Импликация высказываний х,у обозначается сим­волом х ® у , читается «если х,то у»или «из x следует у». Высказывание х называется условием или посылкой, высказывание у – следствием или заключением.

Логические значения операции импликации описы­ваются следующей таблицей истинности:

x	y	х®у

5. Эквиваленция. Эквиваленцей (или эквивалентно­стью) двух высказываний х, у называется новое выска­зывание, которое считается истинным, когда оба выска­зывания х, у либо одновременно истинны, либо одновре­менно ложны, и ложным во всех остальных случаях.

Эквиваленция высказываний х, у обозначается сим­волом х « у, читается «для того, чтобы х,необходимо и достаточно, чтобы у»или «х тогда и только тогда, когда у». Высказывания х, у называются членами эквиваленции.

Логические значения операции эквиваленции опи­сываются следующей таблицей истинности:

x	y	х « у

Формулы алгебры логики

С помощью логических операций над высказывания­ми из заданной сово-купности высказываний можно стро­ить различные сложные высказывания. При этом поря­док выполнения операций указывается скобками. Напри­мер, из трех высказываний х, у, z можно построить выс­казывания

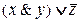и .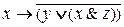

Первое из них есть дизъюнкция конъюнкции х, у и отрицания выказывания z,а второе высказывание есть импликация, посылкой которой является высказывание х, а заключением – отрицание дизъюнкции высказывания у и конъюнкции выска-зываний х, z.

Всякое сложное высказывание, которое может быть получено из элементарных высказываний посредством применения логических операций отрицания, конъюн­кции, дизъюнкции, импликации и эквиваленции, на­зывается формулой алгебры логики.

Формулы алгебры логики обозначаются больши­ми буквами латинского алфавита А, В, С, ...

Для упрощения записи формул принят ряд соглаше­ний. Скобки можно опускать, придерживаясь следую­щего порядка действий: конъюнкция выполняется рань­ше, чем все остальные операции, дизъюнкция выполня­ется раньше, чем импликация и эквивалентность. Если над формулой стоит знак отрицания, то скобки тоже опускаются.

В связи с этим формулы 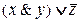и 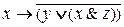могут быть записаны так:

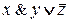и .

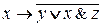Логическое значение формулы алгебры логики пол­ностью определяется логическими значениями входящих в нее элементарных высказываний. Например, логическим значением формулы 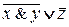в случае, если х = 1, у = 1, z = 0 будет истина, то есть 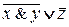= 1.