Упражнение 9. Подберите суждения А, Е, О, сделайте из них выводы путем про­тивопоставления предикату, проверьте правильность вывода с помо­щью превращения и обращения

Подберите суждения А, Е, О, сделайте из них выводы путем про­тивопоставления предикату, проверьте правильность вывода с помо­щью превращения и обращения.

Умозаключения по логическому квадрату

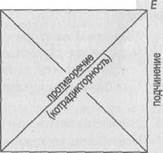
Простые сравнимые суждения, имеющие одинаковые термины и различающиеся по качеству и количеству, находятся в опреде­ленных отношениях, которые иллюстрируются с помощью логиче­ской схемы (логического квадрата) (см. учебник, гл. IV, § 4).

Опираясь на логический квадрат, можно строить выводы, уста­навливая следование истинности или ложности одного суждения из истинности или ложности другого суждения в зависимости от свойств отношений.

Отношение противоречия (кон- противоположность

традикторности): А - О, Е - I. Эти ^ суждения не могут быть одновремен­но ни истинными, ни ложными. Из истинности одного суждения следует £ ложность другого суждения, из лож- 5= ности одного - истинность другого. Л Выводы строятся по схемам: А ~> I О; ^с

(контрарность)

Отношение противоположности

(контрарности): А - Е. Противопо- i частичная совместимость ложные суждения не могут быть од- (субкантрарностъ]

повременно истинными, но могут

быть одновременно ложными. Из истинности одного сужде­ния следует ложность другого, но из ложности одного из них может следовать как истинность, так и ложность другого суж­дения. Выводы строятся по схемам: Л —>~l£";£" —>1Л;~|Л —>(J:v l£);56

Глава 3. Дедуктивные умозаключения

3.1. Непосредственные умозаключения

Отношение частичной совместимости (субконтрарности): I-O, Эти суждения могут быть одновременно истинными, но не могут быть одновременно ложными. Из ложности одного суждения сле­дует истинность другого, но из истинности одного из них может следовать как истинность, так и ложность другого. Выводы строятся по схемам: !/-> О; "1 О ->/; /-> (О v 1 О); О ~> (Jv "]/).

Отношения подчинения: А - /, Е ~ О. Из истинности подчиняюще­го суждения следует истинность подчиненного суждения, но не на­оборот: из истинности подчиненного суждения истинность подчи­няющего суждения не следует, оно может быть истинным, но может быть ложным:А -»/;£-» О; /-> (A v ~U); 0->(£v]f).

Из ложности подчиненного суждения следует ложность подчи­няющего суждения, но не наоборот: из ложности подчиняющего суж­дения ложность подчиненного суждения с необходимостью не следу­ет, оно может быть истинным, но может быть и ложным. ] I -»1 А;