Таблицы истинности составных высказываний
Практическое занятие №2
1 Наименование работы:Логические операции.
2 Цель работы:Научиться составлять и читать высказывания, использовать логические операции в высказываниях, таблицах истинности.
3 Подготовка к занятию: Повторите тему: Логические операции.
4 Литература:
4.1 Конспект лекций по учебной дисциплине «Элементы математической логики»
4.2 Приложение к ПЗ №2.
5 Перечень необходимого оборудования и материалов:
5.1 Бланк для отчета.
5.2 Канцелярские принадлежности.
6 Задание на занятие:
Основная часть
6.1 Постройте таблицы истинности для пунктов задания 6.2 и 6.3 ПЗ № 1. Укажите тавтологии и опровержения, если таковые имеются.
6.2 Постройте таблицы истинности для следующих выражений и определите, являются ли они тавтологией или противоречием (опровержением).
1) 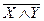 ;
;
2) 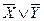 ;
;
3) 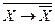 .
.
6.3 Проверьте, пользуясь таблицами истинности, эквивалентность следующих высказываний. Определите, являются ли они противоречием или тавтологией.
а) 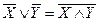 ; в)
; в) 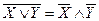 ;
;
б) 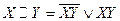 ; г)
; г) 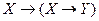 .
.
6.4 В каких случаях приведенные ниже данные противоречивы?
1) A= 1, 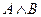 = 1
= 1
2) A= 0, 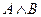 = 1
= 1
3) A= 1, 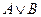 = 0
= 0
4) A= 0, 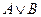 = 1
= 1
Вариативная часть:
6.5 Известно, что 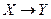 имеет значение 1. Что можно сказать о значениях нижеприведенных выражений? Объясните, почему?
имеет значение 1. Что можно сказать о значениях нижеприведенных выражений? Объясните, почему?
а) 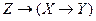 ;
;
б) 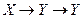 ;
;
в) 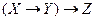 .
.
6.6 Докажите тождественную истинность выражения 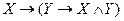
6.7 При каких значениях переменных P,Q,R следующие выражения ложны? Объясните, почему.
1) 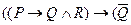
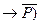
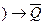 ;
;
2) 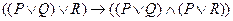 ;
;
3) 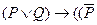
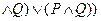
7 Порядок выполнения работы:
Выполните практическую работу в соответствии с заданиями (основная часть п.п. 6.1 – 6.4) и сдайте зачет. В случае получения зачета, выполните вариативную часть (п.п.6.5 – 6.6).
8 Содержание отчета:
Решения задач в соответствии с заданием.
9 Контрольные вопросы:
1 Что такое тавтология, опровержение?
2 Постройте таблицы истинности для логических операций: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция.
3 В каком порядке при отсутствии скобок выполняются логические операции?
4 Какие формулы алгебры высказываний являются эквивалентными?
Приложение к практическому занятию по ЭМЛ № 2
Таблицы истинности составных высказываний
При рассмотрении той или иной связки мы хотим знать, каким именно образом истинность составного высказывания, порожденного этой связкой, зависит от истинности его компонент. Очень удобно изображать эту зависимость, пользуясь таблицами истинности, которые называются также интерпретациями логических операций. Каждой строке таблицы истинности взаимно однозначно соответствует набор составляющих высказываний и соответствующее значение составного высказывания. Наборы из нулей и единиц, соответствующих составляющим высказываниям, в каждой строке таблицы истинности имеют стандартное расположение, т.е. расположены в лексикографическом порядке (порядке возрастания).
Таблица истинности высказывания, составленного из двух простых высказываний, состоит из четырех строк; а таблица истинности высказывания, составленного из трех простых высказывания - из восьми строк. Сколько строк должна иметь таблица истинности высказывания, составленного из четырех простых высказываний? Сколько – из пяти? Сколько из n?
Для систематической записи таблиц истинности для произвольного n можно применить метод «последовательного половинного деления столбцов» - столбец первой переменной делят пополам и заполняют верхнюю половину нулями, а нижнюю половину – единицами, затем каждую половину второго столбца делят пополам и опять заполняют полученные половины нулями и единицами и т.д.
Каждая формула алгебры высказываний обладает свойством превращаться в высказывание при фиксации в ней значений всех высказывательных переменных, т.е. если мы зафиксируем в формуле значения всех высказывательных переменных, то, пользуясь определениями логических операций, мы можем вычислить значение истинности формулы.
Таблица истинности формулы алгебры высказываний содержит столько строк, сколько всевозможных наборов значений истинности переменных можно образовать. Так как каждая высказывательная переменная может принимать только два значения (0 и 1), то в случае n переменных таблица истинности содержит 2n строк.
При построении таблицы истинности наборы значений переменных располагают сверху вниз в лексикографическом порядке (каждый набор понимают как двоичную запись неотрицательного целого числа и располагают в порядке возрастания от (000…0) до (111…1)).
Если возникают трудности с использованием двоичной системы счисления, можно применить метод «последовательного половинного деления столбцов» - столбец первой переменной делят пополам и заполняют верхнюю половину нулями, а нижнюю половину – единицами, затем каждую половину второго столбца делят пополам и опять заполняют полученные половины нулями и единицами, и т.д. Последовательность такого заполнения приведена на рис 1.
Затем в соответствии с порядком действий последовательно заполняют столбцы значений подформул, из которых образуется формула. Последним заполняется столбец значений истинности формулы.
| x1 | x2 | x3 |
| x1 | x2 | x3 |
| x1 | x2 | x3 |
рис.1
Пример 1. Построить таблицу истинности формулы: x1 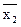
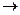 (x1
(x1  x2)
x2) 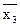
1. Определим порядок действий в формуле:
1) 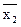
2) x1 × 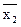
3) (x1 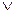 x2)
x2)
4) 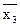
5) (x1 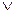 x2)×
x2)× 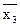
6) x1 × 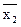
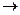 (x1
(x1 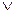 x2)×
x2)× 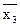
2. Пользуясь определениями логических операций Ø, &, Ú и ® заполним таблицу.
Таблица.
| x1 | x2 | x3 | 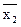 | x1× 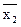 | x1 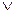 x2 x2 | 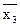 | (x1 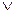 x2) x2) 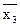 | x1 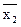 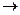 (x1 (x1 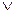 x2) x2) 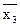 |
