Закон исключенного третьего 13 страница
Объединение графов 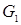 и
и 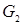 называется дизъюнктным, если
называется дизъюнктным, если 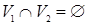 .
.
Операция объединения обладает следующими свойствами, которые следуют из определения операции и свойств операций на множествах:
1. 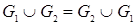 – свойство коммутативности;
– свойство коммутативности;
2. 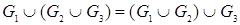 – свойство ассоциативности.
– свойство ассоциативности.
Операция объединения графов может быть выполнена в матричной форме. Для графов с одним и тем же множеством вершин справедлива следующая теорема.
Теорема 19.1.Пусть 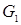 и
и 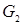 – два графа (ориентированные или не ориентированные одновременно) с одним и тем же множеством вершин
– два графа (ориентированные или не ориентированные одновременно) с одним и тем же множеством вершин  , и пусть
, и пусть 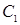 и
и 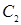 – матрицы смежности вершин этих графов. Тогда матрицей смежности вершин графа
– матрицы смежности вершин этих графов. Тогда матрицей смежности вершин графа 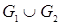 является матрица
является матрица 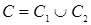 , образованная поэлементным логическим сложением матриц
, образованная поэлементным логическим сложением матриц 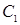 и
и 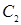 .
.
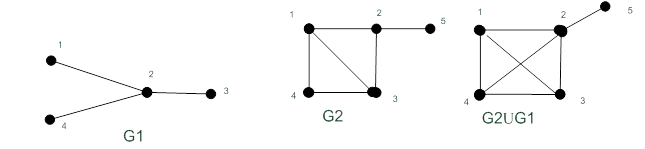
Рисунок 19.6 – Объединение графов
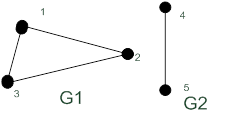
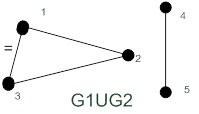
Рисунок 19.7 – Дизъюнктное объединение графов
19.1.5 Пересечение графов
Определение. Пусть 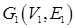 и
и 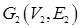 – произвольные графы. Пересечением
– произвольные графы. Пересечением 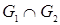 графов
графов 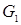 и
и 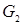 называется граф с множеством вершин
называется граф с множеством вершин 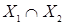 с множеством ребер (дуг)
с множеством ребер (дуг) 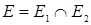 .
.
Операция пересечения обладает следующими свойствами, которые следуют из определения операции и свойств операций на множествах:
1. 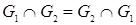 – свойство коммутативности;
– свойство коммутативности;
2. 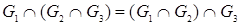 – свойство ассоциативности.
– свойство ассоциативности.
Для того чтобы операция пересечения была всеобъемлющей, необходимо ввести понятие пустого графа.
Определение. Граф 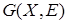 называется пустым, если множество
называется пустым, если множество  вершин графа является пустым (
вершин графа является пустым ( 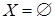 ). Заметим, что в этом случае и множество
). Заметим, что в этом случае и множество 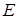 ребер (дуг) графа также пустое множество (
ребер (дуг) графа также пустое множество ( 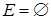 ). Пустой граф обозначается символом
). Пустой граф обозначается символом 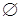 . Такой граф может быть получен в результате выполнения операции пересечения графов, у которых
. Такой граф может быть получен в результате выполнения операции пересечения графов, у которых 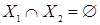 . В этом случае говорят о непересекающихся графах.
. В этом случае говорят о непересекающихся графах.
Теорема 19.2. 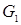 и
и 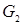 – два графа (ориентированные или неориентированные одновременно) с одним и тем же множеством вершин
– два графа (ориентированные или неориентированные одновременно) с одним и тем же множеством вершин  , и пусть
, и пусть 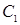 и
и 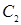 – матрицы смежности вершин этих графов. Тогда матрицей смежности вершин графа
– матрицы смежности вершин этих графов. Тогда матрицей смежности вершин графа 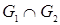 является матрица
является матрица 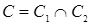 , образованная поэлементным логическим умножением матриц
, образованная поэлементным логическим умножением матриц 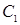 и
и 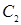 .
.
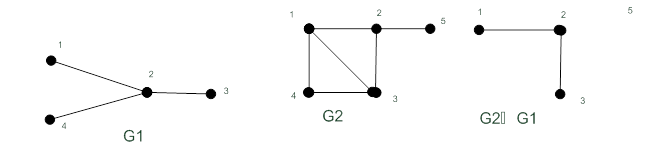
Рисунок 19.8 – Пересечение графов
19.1.6 Соединение графов
Определение. Соединением (сильным произведением) графов 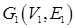 и
и 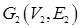 (
( 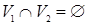 ) называют граф такой, что
) называют граф такой, что 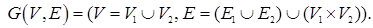
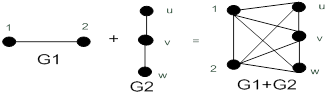
Рисунок 19.9 – Соединение графов
19.1.7 Композиция графов
Определение. Пусть 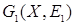 и
и 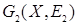 – два графа с одним и тем же множеством вершин
– два графа с одним и тем же множеством вершин  . Композицией
. Композицией 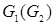 графов
графов 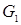 и
и 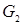 называется граф с множеством вершин
называется граф с множеством вершин 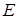 , в котором существует дуга
, в котором существует дуга 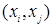 тогда и только тогда, когда существует дуга
тогда и только тогда, когда существует дуга 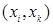 , принадлежащая множеству
, принадлежащая множеству 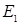 , и дуга
, и дуга 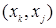 , принадлежащая множеству
, принадлежащая множеству 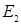 .
.
Пример.Рассмотрим выполнение операции композиции 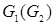 на графах, изображенных на рис. 6.25.
на графах, изображенных на рис. 6.25.
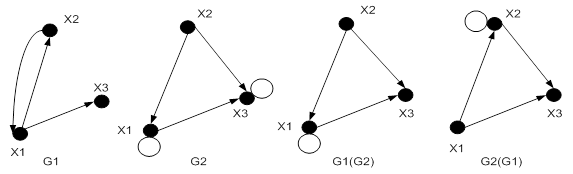
Рисунок 19.10 – Композиция графов
Для рассмотрения операции составим таблицу 19.1, в первом столбце которой указываются ребра 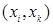 , принадлежащие графу
, принадлежащие графу 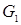 , во втором — ребра
, во втором — ребра 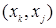 , принадлежащие графу
, принадлежащие графу 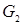 , а в третьем — результирующее ребро
, а в третьем — результирующее ребро 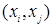 для графа
для графа 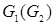 .
.
Таблица 19.1 – Построение композиции графов 
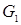 | 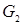 | 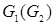 |
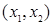 | 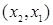  | 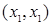 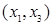 |
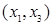 | 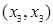 | 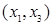 |
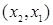 | 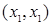 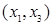 | 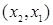  |
Заметим, что дуга 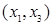 результирующего графа в таблице встречается дважды. Однако, поскольку рассматриваются графы без параллельных ребер (дуг), то в множестве E результирующего графа дуга
результирующего графа в таблице встречается дважды. Однако, поскольку рассматриваются графы без параллельных ребер (дуг), то в множестве E результирующего графа дуга 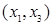 учитывается только один раз, т.е.
учитывается только один раз, т.е. 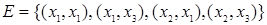 .
.
На рис. 19.10 изображены графы 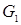 и
и 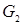 и их композиция
и их композиция 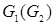 . На этом же рисунке изображен граф
. На этом же рисунке изображен граф 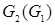 . Рекомендуется самостоятельно построить граф
. Рекомендуется самостоятельно построить граф 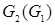 , и убедиться, что графы
, и убедиться, что графы 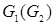 и
и 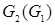 не изоморфны.
не изоморфны.
19.1.8 Произведение графов
Определение. Декартовым произведением 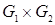 называется граф
называется граф  , для которого
, для которого 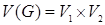 – декартово произведение множеств вершин исходных графов, а
– декартово произведение множеств вершин исходных графов, а 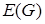 определяется следующим образом: вершины
определяется следующим образом: вершины 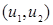 и
и 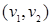 смежны в графе
смежны в графе 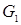 тогда и только тогда, когда или
тогда и только тогда, когда или 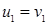 ,а
,а 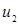 и
и 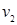 смежны в
смежны в 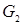 , или
, или 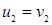 ,а
,а 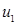 и
и 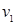 смежны в
смежны в 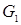 .
.
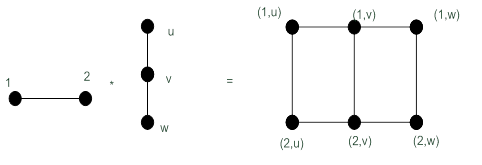
Рисунок 19.11 – Декартово произведение графов
19.2 Гомеоморфные графы
Два графа называются гомеоморфнымиили тождественными с точностью до вершины степени 2, если они могут быть получены из одного и того же графа с помощью операции ведения вершины степени 2 в ребро.На рисунке 19.12 показаны гомеоморфные графы.
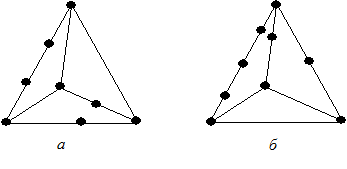
Рисунок 19.21 – Гомеоморфные графы
19.3 Плоские и планарные графы
Все изображения графа являются изоморфными и несут одну и ту же информацию. Однако встречаются ситуации, когда крайне важно, чтобы изображение графа на плоскости удовлетворяло определенным требованиям.
Например, в радиоэлектронике при изготовлении микросхем печатным способом электрические цепи наносятся на поверхность изоляционного материала. А так как проводники не изолированы, то они не должны пересекаться. Аналогичная задача возникает при проектировании железнодорожных и иных путей, где нежелательны переезды.
Определение. Геометрический граф назовем плоским графом, если он нарисован на плоскости так, что все линии, изображающие его ребра, пересекаются только в точках, соответствующих вершинам графа, т.е. любая точка пересечения таких линий, есть вершина, инцидентная ребрам, которые эти линии изображают. Любой граф, изоморфный плоскому графу, называют планарным.
О планарных графах говорят, что они укладываются на плоскости (имеют плоскую укладку) (рис. 19.22). Планарный граф можно уложить на плоскости, а плоский граф – это граф, уже уложенный на плоскости. Плоский граф есть изображение планарного графа, однако не каждое изображение планарного графа является плоским графом.
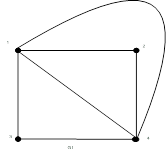
Рисунок 19.22 – Плоский граф
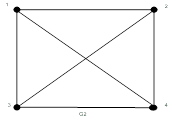
Рисунок 19.23 – Планарный граф
Пример плоского графа приведен на рис. 19.22. Изоморфный ему полный граф 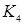 (рис. 19.23), укладываемый на плоскости, имеет два пересекающихся ребра, поэтому граф
(рис. 19.23), укладываемый на плоскости, имеет два пересекающихся ребра, поэтому граф 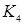 не является плоским – он только планарный.
не является плоским – он только планарный.
19.3.1 Теорема Понтрягина – Куратовского
Теорема Понтрягина – Куратовского гласит: граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных 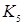 и
и 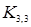 , где
, где 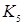 – полный 5-вершинный граф, а
– полный 5-вершинный граф, а 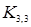 – полный двудольный граф, каждая доля которого состоит из 3 вершин. Граф
– полный двудольный граф, каждая доля которого состоит из 3 вершин. Граф 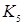 представляет собой полный граф наименьшего порядка, который, не являясь планарным графом (полные графы
представляет собой полный граф наименьшего порядка, который, не являясь планарным графом (полные графы 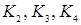 – планарные), становится планарным после удаления хотя бы одного его ребра. Второй (двудольный граф
– планарные), становится планарным после удаления хотя бы одного его ребра. Второй (двудольный граф 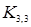 ) является моделью известной задачи о трех домах и трех колодцах.
) является моделью известной задачи о трех домах и трех колодцах.
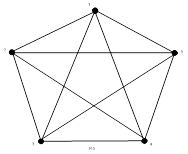
Рисунок 19.24 – 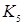 – полный 5-вершинный граф
– полный 5-вершинный граф
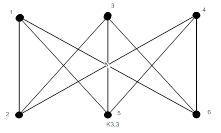
Рисунок 19.25 – 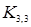 – полный двудольный граф
– полный двудольный граф
Определение. Жордановой кривойна плоскости называется непрерывная кривая линия без самопересечений. Замкнутая жорданова кривая – это жорданова кривая, начало и конец которой совпадают.


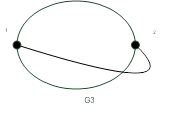
Рисунок 19.26 – Примеры жордановых кривых
Теорема Жордана: Если  замкнутая жорданова кривая, то всякая жорданова кривая, соединяющая точки 1 и 2, лежащие на
замкнутая жорданова кривая, то всякая жорданова кривая, соединяющая точки 1 и 2, лежащие на  , либо полностью лежит внутри
, либо полностью лежит внутри  (рис. 19.26 граф
(рис. 19.26 граф  ), либо вне
), либо вне  (рис. 19.26 граф
(рис. 19.26 граф  ), либо пересекает
), либо пересекает  в одной единственной точке отличной от 1 и 2 (рис. 19.26 граф
в одной единственной точке отличной от 1 и 2 (рис. 19.26 граф  ).
).
19.3.2 Построение плоского изображения графа. Гамма-алгоритм
Для плоской укладки графа и попутной проверки, планарный ли он, удобно пользоваться гамма-алгоритмом.
На вход подаются графы, обладающие следующими свойствами:
1. Граф связный.
2. Граф имеет хотя бы один цикл.
3. Граф не имеет мостов, т. е. ребер, после удаления которых граф распадается на две компоненты связности.
Если нарушено свойство (1), то граф нужно укладывать отдельно по компонентам связности.
Если нарушено свойство (2), то граф – дерево и нарисовать его плоскую укладку тривиально.
Случай нарушения свойства (3) рассмотрим более подробно. Если в графе есть мосты, то их нужно разрезать, провести отдельно плоскую укладку каждой компоненты связности, а затем соединить их мостами. Здесь может возникнуть трудность: в процессе укладки концевые вершины моста могут спрятаться внутри плоского графа. Нарисуем одну компоненту связности и будем присоединять к ней другие последовательно. Каждую новую компоненту связности будем рисовать в той грани, в которой лежит концевая вершина соответствующего моста. Так как граф связности мостами компонент связности является деревом, мы сумеем получить плоскую укладку.
Сначала рассмотрим алгоритм на конкретном примере. Пусть дан граф  (рис. 19.27).
(рис. 19.27).
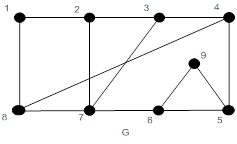
Рисунок 19.27
Инициализация алгоритма производится так: выбираем любой простой цикл; в нашем примере {1, 2, 3, 4, 5, 6, 7, 8} и получаем две грани: 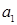 – внешнюю и
– внешнюю и 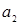 – внутреннюю (см. рис. 19.28).
– внутреннюю (см. рис. 19.28).
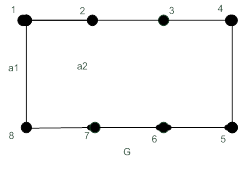
Рисунок 19.28
Обозначим выбранный цикл как 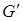 . На каждом шаге будем строить множество сегментов. Каждый сегмент S относительно уже построенного графа
. На каждом шаге будем строить множество сегментов. Каждый сегмент S относительно уже построенного графа 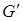 представляет собой одно из двух:
представляет собой одно из двух:
- ребро, оба конца которого принадлежат 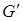 , но само оно не принадлежит
, но само оно не принадлежит 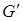 ;
;
- связную компоненту графа 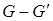 , дополненную всеми ребрами графа
, дополненную всеми ребрами графа  , один из концов которых принадлежит связной компоненте, а второй из графа
, один из концов которых принадлежит связной компоненте, а второй из графа 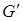 .
.
Те вершины, которые одновременно принадлежат 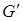 и какому-то сегменту, назовем контактными. Для нашего примера сегменты и вершины изображены на рис. 19.29. Контактные вершины обведены в квадрат.
и какому-то сегменту, назовем контактными. Для нашего примера сегменты и вершины изображены на рис. 19.29. Контактные вершины обведены в квадрат.
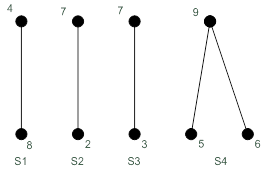
Рисунок 19.29
Если бы в каком-нибудь сегменте не было ни одной контактной вершины, то граф до разрезания был бы несвязный; если бы была только одна, то граф имел бы мост. Эти возможности заранее исключены, так что каждый сегмент имеет не менее двух контактных вершин. Поэтому в каждом сегменте имеется цепь между любой парой таких вершин.
Если все контактные вершины сегмента  имеют номера вершин какой-то грани
имеют номера вершин какой-то грани 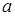 , то мы будем говорить, что грань
, то мы будем говорить, что грань 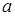 вмещает этот сегмент и обозначать
вмещает этот сегмент и обозначать 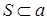 . Может быть имеется не одна такая грань, вмещающая сегмент
. Может быть имеется не одна такая грань, вмещающая сегмент  , множество таких граней обозначим
, множество таких граней обозначим 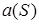 , а их число
, а их число 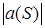 .
.
Общий шаг алгоритма следующий: обозреваются все сегменты 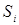 и определяются числа
и определяются числа 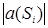 . Если хоть одно из них равно 0, то граф не планарен, конец. Иначе, выбираем сегмент, для которого число
. Если хоть одно из них равно 0, то граф не планарен, конец. Иначе, выбираем сегмент, для которого число 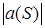 минимально, или один из множества, если таких сегментов несколько. В этом сегменте найдем цепь между двумя контактными вершинами и уложим ее в любую из граней множества а(S), совместив контактные вершины сегмента с соответствующими вершинами грани. При этом данная грань разобьется на две. Уже уложенная часть графа
минимально, или один из множества, если таких сегментов несколько. В этом сегменте найдем цепь между двумя контактными вершинами и уложим ее в любую из граней множества а(S), совместив контактные вершины сегмента с соответствующими вершинами грани. При этом данная грань разобьется на две. Уже уложенная часть графа 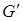 по количеству ребер и вершин увеличится, а сегмент, из которого вынута цепь, исчезнет или развалится на меньшие с новыми контактными вершинами, ведущими к вершинам
по количеству ребер и вершин увеличится, а сегмент, из которого вынута цепь, исчезнет или развалится на меньшие с новыми контактными вершинами, ведущими к вершинам 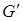 .
.
В результате повторения общего шага либо будет получена плоская укладка, когда множество сегментов станет пустым, либо будет получено, что граф G не является планарным. Вернемся к нашему примеру.
Пока 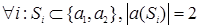 . Поэтому возьмем первый по номеру сегмент
. Поэтому возьмем первый по номеру сегмент 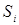 и в нем первую попавшеюся цепь {4, 8}; вставим эту цепь в грань
и в нем первую попавшеюся цепь {4, 8}; вставим эту цепь в грань 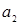 Получим увеличенную часть
Получим увеличенную часть 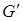 и уменьшенную систему сегментов (см. рис. 19.30 А), В)).
и уменьшенную систему сегментов (см. рис. 19.30 А), В)).
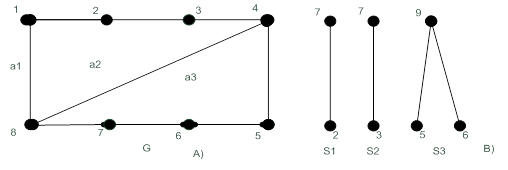
Рисунок 19.30
Определим, какие грани вмещают новые сегменты. Теперь сегменты 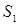 и
и 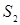 вмещаются только в одну грань
вмещаются только в одну грань 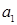 , в то время, как сегмент
, в то время, как сегмент 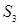 вмещается в две грани а1 и а3. Поэтому берем
вмещается в две грани а1 и а3. Поэтому берем 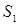 . Возьмем в нем цепь между контактными вершинами, например, {2, 7}, и уложим ее в
. Возьмем в нем цепь между контактными вершинами, например, {2, 7}, и уложим ее в 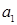 . Получим увеличенную часть
. Получим увеличенную часть 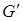 и уменьшенную систему сегментов (рис. 19.31 А), В)).
и уменьшенную систему сегментов (рис. 19.31 А), В)).
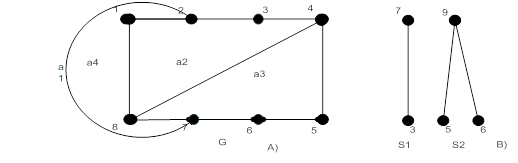
Рисунок 19.31
Продолжая таким образом, в итоге получим плоскую укладку G (рис. 19.32).
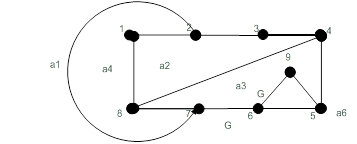
Рисунок 19.32
