Циклический избыточный код

Разнообразные циклические избыточные коды (CRC – Cyclic Redundancy Cod) используются почти всеми канальными протоколами для формирования контрольных последовательностей кадров. Определение этих кодов как циклических связано с тем, что если B_k(b₀,b₁,…,b_n-1) - кодовое слово, то и B_i(b_n-1,b₀,…,b_n-2) – также допустимое кодовое слово. Эти коды относится к классу, так называемых, полиномиальных кодов. Такое название они получили потому, что формирование кодового слова реализуется посредством алгебры полиномов с двоичными коэффициентами.

Особенности используемой алгебры двоичных полиномов иллюстрируются следующими примерами.

· Сложение

· Умножение

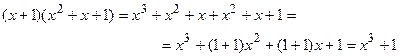
· Деление

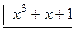
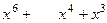- частное

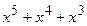
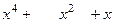
x ← остаток

Итак, k информационных бит ( 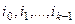) используются для формирования информационного полинома степени k-1

.

В результате кодирования последовательности ( 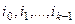) формируется кодовое слово из n бит. Из битов кодового слова можно сформировать полиномом b(x) степени n-1>k-1.

Правило кодирования строится так, что полином b(x) удовлетворяет вполне определенному условию, именно – он делится без остатка на заранее определенный (известный передатчику и приемнику) полином g(x), который называется порождающим. Одним из обязательных свойств этого полинома является отличие от нуля коэффициентов при старшей и нулевой степенях .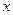

Будем считать, что формируется кодовое слово длиной n бит, из которых k - информационные и (n - k) – контрольные биты. Такой код будем обозначать дуплетом (n, k). Для формирования кодового слова используется порождающий полином степени n – k

,

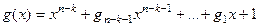где 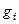- двоичные числа.

Формирование полинома b(x), т.е. вычисление проверочных битов (битов CRC), производится по следующему алгоритму.

Ш1. Умножить 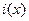на . В результирующем полиноме степени (n-1) коэффициенты при 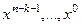положить равными нулю.

Ш2. Разделить полином на порождающий полином g(x) и определить остаток .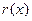

.

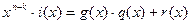Ш3. Прибавить остато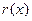к к , т.е. добавить биты CRC в (n – k) младших разрядов представления полинома .

Полином 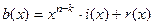делится без остатка на . Действительно

.

Здесь учтена особенность арифметики по модулю 2, при которой

.

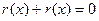Коэффициенты полинома 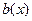образуют кодовое слово, подлежащее передаче по коммуникационному каналу. При этом, любое кодовое слово кратно порождающему полиному.

Проиллюстрируем процесс формирования CRC-последовательности на примере кода (7,4) с порождающим полиномом и информационной последовательностью вида (1,1,0,0). Информационный полиномом в этом случае имеет вид .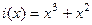

Ш1. n – k = 3

Коэффициенты этого полинома образуют последовательность (1,1,0,0,0,0,0).

Ш2. 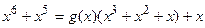(смотри приведенный выше пример деления полиномов).

Следовательно, .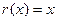

Ш3. 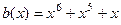, что соответствует кодовому слову (1,1,0,0,0,1,0). Заметим, что в полученном кодовом слове старшие четыре разряда соответствуют информационным битам, а младшие три – биты CRC.

Приемное устройство, сформировав на основе принятой последовательности из n бит полином 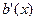и выполнив операцию его деления на порождающий полином , по признаку наличия остатка от деления может индицировать наличие ошибки в принятом блоке данных.

Рассмотрим виды ошибок, которые не могут быть обнаружены проверкой CRC-битов кодовых слов. Представим канал аддитивной моделью (рис.3.3), в которой кодовое слово 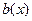суммируется по модулю 2 без переноса с полиномом ошибок .

Для аддитивной модели будет справедливым выражение

.

Из него хорошо видно, что если полином делится без остатка на , то ошибки обнаружены не будут.

Построение порождающего полинома, прежде всего, подчиняется условию обнаружения определенного вида ошибок. Пусть таким условием является обнаружение всех возможных единичных ошибок. Будем считать, что искажен j-й бит. Тогда полином ошибки является одночленом вида

.

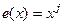Поскольку порождающий полином содержит, как минимум, два слагаемых (коэффициенты при 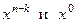равны 1), то при умножении его на любой другой полином результат будет содержать не менее двух слагаемых. Следовательно, полином 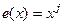не может нацело делиться на любой порождающий полином, и все единичные ошибки полиномиальными кодами будут обнаруживаться.

Парные ошибки. Полином ошибки имеет вид

.

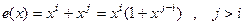Как отмечено выше, 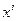не делится без остатка на . Следовательно, разделится на только в случае, когда будет кратен . Таким образом, необходимо использовать порождающий полином , не являющийся делителем полинома 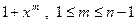. Существует класс, так называемых, примитивных полиномов, одним из свойств которых является их невозможность быть делителями полиномов вида 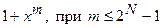, где N – степень примитивного полинома. Следовательно, для обнаружения всех парных ошибок в кодовых словах длинной n, порождающий полином следует выбрать из класса примитивных полиномов степени N, удовлетворяющей неравенству .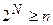

Если в принятом слове окажутся инвертированными нечетное число битов, то полином будет содержать нечетное число слагаемых ( 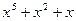, например). В системе операций по модулю 2 нет многочленов с нечетным числом членов, делящихся на многочлен . Следовательно, если порождающий полином будет кратен такому полиному, то с его помощью будут обнаружены все ошибочные слова с нечетным числом ошибок.

По этим критериям сформирован ряд широко использующихся на практике порождающих полиномов вида 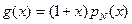, где 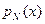- примитивный полином. Так, например, порождающий полином кода CRC-16 имеет вид

.

Еще одним важным видом ошибок является поражение последовательности L бит в кодовом слове длиной n бит. Можно показать, что если степень порождающего полинома (n-k) и 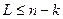, то все ошибки будут обнаружены. При не будет обнаружена (1/2^n-k) часть всех возможных ошибок.

Применение приведенного выше порождающего полинома 16 порядка позволяет детектировать все одинарные и парные ошибки, а также ошибки в нечетном количестве бит в кодовых словах, длина которых не превосходит 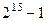= 32767 бит. Заметим, что в последовательности из 32767 бит контрольными являются не более 16 бит, т.е. избыточность такого кода оказывается весьма низкой.

Примеры порождающих полиномов, используемых наиболее известными телекоммуникационными протоколами, приведены в таблице 3.1.

Таблица 3.1

Название	Полином	Используется в
CRC-8		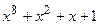ATM, заголовок
CRC-10		ATM, кадр подуровня AAL
CCITT CRC-16		HDLC, V.41
CCITT CRC-32		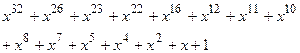IEEE 802, V.42

Контрольные задания