Методические указания к заданию 2
Следует обратить внимание на терминологию, используемую в данной работе.
Понятие «формирование логического выражения» практически эквивалентно понятию «синтез цифрового устройства», так как на основании имеющегося математического выражения легко реализовать конкретное устройство. Другими словами: говоря о минимизации логического выражения (уменьшении размера математической формулы) мы говорим и о минимизации цифрового устройства (о сокращении аппаратных затрат на его реализацию). Чем компактнее логическое выражение, тем меньшее число микросхем требуется на реализацию конкретного КЦУ.
В процессе выполнения данной работы каждый студент создает устройство, которое работает в соответствии с таблицей 1. Причем вначале создается математическое описание этой таблицы (математическая модель), а затем на основании математического описания реализуется устройство.
Структурная схема синтезируемого устройства показана на рисунке.
Механизм получения логических выражений с помощью прибора Logic Converter (Логического конвертора) скрыт от пользователя. Пользователь в процессе синтеза устройства получает лишь конечный результат (формулу) на основании введенной таблицы истинности и не знает, как эта формула получена.
Рассмотрим два способа формирования математических моделей КЦУ: аналитический (алгебраический) и графо-аналитический.
Опишем аналитически устройство, алгоритм работы которого задан с помощью табл. 2 (вариант № 16).
Таблица 2
| Номера состояний | Входные сигналы преобразователя кода | Выходной сигнал Y | |||
| A | B | C | D | ||
| Х | |||||
| Х | |||||
| Х | |||||
| Х | |||||
| Х | |||||
В таблице 2 каждому состоянию устройства соответствует один набор аргументов A, B, C, D (один минтерм).
Аналитическое (алгебраическое) описание произведем с помощью совершенной дизъюнктивной нормальной формы (СДНФ). СДНФ представляет собой сумму минтермов, для которых выходной сигнал равен логической единице.
Совершенная дизъюнктивная нормальная форма имеет такое название потому, что она совершенна: все слагаемые (минтермы) имеют одинаковую размерность (в данном случае число переменных равно четырем). СДНФ представляет собой сумму (дизъюнкцию) минтермов. При составлении СДНФ использовано только три логические операции (дизъюнкция, конъюнкция и инверсия). По этой причине она названа нормальной.
Из таблицы 2 видно, что выходной сигнал Y принимает значение логической единицы в состояниях 4, 10, 11, 12, 13 и 14. Таким образом, аналитическое выражение будет содержать шесть слагаемых (шесть минтермов). Для правильной записи минтермов нужно использовать следующее правило. Входная переменная (аргумент) берется без инверсии, если она равна 1 и берется с инверсией, если равна 0. Таким образом, минтерм для состояния 4 должен быть записан так:
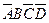
Поступая аналогично с другими пятью минтермами, получим аналитическое выражение, которое описывает работу преобразователя кода:
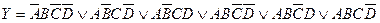
Сопоставление полученного выражения с выражением, сформированным автоматически с помощью прибора Logic Converter, показывает, что они идентичны.
Рассмотрим процедуру получения математической модели графическим способом с помощью диаграмм Вейча. Аналогичный результат можно получить и с помощью Карт Карно. Эти две методики минимизации комбинационных цифровых устройств (КЦУ) отличаются незначительно (лишь порядком маркировки таблиц).
Порядок использования диаграмм Вейча рассмотрим на примере варианта №16 (см. табл. 1 и табл. 2).
На следующей диаграмме показано, в какую клетку диаграммы Вейча нужно заносить значение выходного сигнала в зависимости от номера состояния (номера минтерма).
Таблица 3
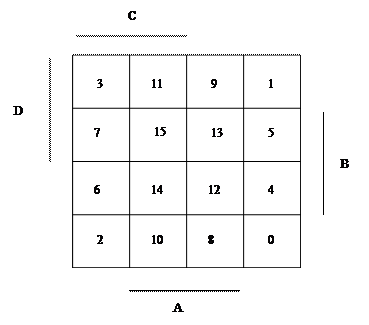
Прямые линии и буквы рядом с таблицей 3 показывают, в каких состояниях данная переменная принимает значение логической единицы. Например, переменная D принимает значение логической единицы в состояниях 3, 11, 9, 1, 7, 15, 13, 5. Это, действительно, так. Младший разряд двоичного числа равен единицы для всех нечетных чисел.
На следующем этапе графического синтеза устройства нужно в каждую клетку таблицы 3 занести соответствующие выходные сигналы из таблицы 2. Ниже представлен результат переноса выходных сигналов из табл. 2 в табл. 3.
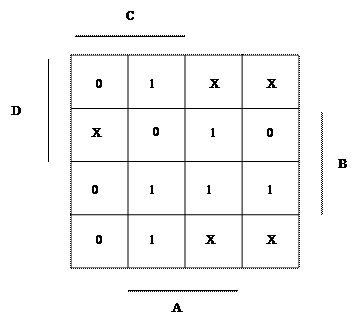Таблица 4
После выполненного переноса нужно охватить контурами все клетки (ячейки), которые содержат единицы (см. таблицу 4). Перечислим правила, которыми следует руководствоваться при формировании контуров.
1. Объединять можно соседние (смежные) по столбцам или строкам ячейки, которые содержат единицы, контурами, охватывающими 2, 4, 8, 16…2n ячеек.
2. Контуры могут объединять ячейки, расположенные на противоположных сторонах диаграммы (таблицы).
3. Одна и та же ячейка может несколько раз входить в различные контуры.
4. При охвате ячеек контурами следует стремиться к тому, чтобы контур был как можно больше, а число контуров было минимальным.
5. В контур запрещено включать ячейки, содержащие нули, однако допустимо включать ячейки, выделенные знаками безразличного состояния.
6. Ячейки, отмеченные знаками безразличного состояния, могут быть не охвачены контурами.
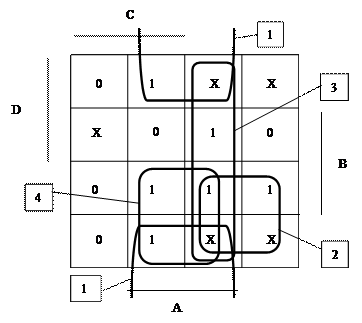Таблица 5
Предыдущий рисунок показывает, что потребовалось четыре контура для охвата шести клеток с единицами. Это означает, что в итоговом алгебраическом выражении будет четыре слагаемых (четыре импликанты). Следует обратить внимание, что контуры включают в себя не только ячейки, содержащие единицы, но и ячейки со знаками безразличного состояния. Еще одна любопытная особенность рассматриваемого устройства: контур № 1 начинается на верхней стороне таблицы, а заканчивается на нижней стороне. Считается, что вертикальные стороны таблицы совмещены друг с другом (также соседними являются горизонтальные стороны таблицы). Интересно, что единица, расположенная в ячейке № 12 , входит одновременно в три контура (это допустимо).
После выполнения графических построений необходимо каждый контур описать алгебраическим выражением. При составлении формул необходимо руководствоваться следующими правилами.
В итоговое выражение (в сокращенную дизъюнктивную нормальную форму) должны войти следующие слагаемые.
1. Минтермы, которые описывают отдельные клетки с единицами, не вошедшие ни в один контур.
2. Импликанты, число которых равно числу контуров.
При составлении выражений, которые описывают ячейки, объединенные контуром, следует отбрасывать те аргументы, границы которых пересекаются контуром.
