Б) Доказательство с дополнительным построением.

Рассмотрим теорему: «Средняя линия трапеции параллельна основаниям и равна их полусумме».

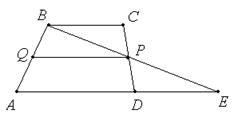Дано: АВСD – трапеция.

Доказать: QP || BC, QP || AD, QP=(BC+AD)/2.

Доказательство:

1. Проведём BP AD=E, где Р – середина CD.

2. Треугольники PBC и PED равны по 2-ому признаку (CP=DP по построению, углы при вершине P равны как вертикальные, углы C и D равны как накрест лежащие).

3. PB=PE, BC=ED.

4. PQ – средняя линия треугольника ABE.

5. PQ || AE, причём PQ=AE/2=(AD+BC)/2, ч.т.д.

в) Доказательство с посредником (например, доказательство признаков равенства треугольников).

г) Доказательство с помощью контрпримеров– используется для доказательства ложности какой-либо теоремы (часто обратной данной). Чтобы убедиться в ложности суждения, достаточно привести пример, где бы это суждение было ложным.

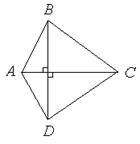
Например, теорема (свойство ромба): «У ромба диагонали взаимно перпендикулярны». Обратная теорема: «Если в четырёхугольнике диагонали взаимно перпендикулярны, то он является ромбом». Обратная теорема ложна, т.к. легко привести контрпример (построим четырёхугольник, у которого диагонали взаимно перпендикулярны, а ромбом он не является – см. рис.2).

6. Методика обучения доказательству.

Поиск доказательства идёт стандартно двумя методами:

1. Анализ Паппа (восходящий анализ) – ведущим вопросом является вопрос: «Что достаточно знать, чтобы ответить на поставленный вопрос?».

2. Анализ Евклида (нисходящий анализ) – рассуждения начинаются так: «Временно предположим, что то, что нам нужно доказать, уже доказано. Что отсюда следует?».

Например, дана теорема (признак параллелограмма): «Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм».

Восходящий анализ.

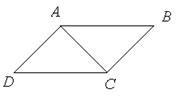1. Для доказательства того, что ABCD – параллелограмм, достаточно доказать, что BC || AD и AB || DC.

2. Для доказательства параллельности сторон четырёхугольника достаточно доказать равенство накрест лежащих углов при параллельных прямых и секущей.

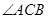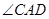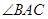3. Такие накрест лежащие углы можно получить, если провести диагональ АС: и , и .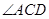

4. Для доказательства равенства накрест лежащих углов достаточно доказать равенство треугольников АВС и СDA.

5. Для доказательства равенства данных треугольников достаточно установить справедливость равенств: BC=DA, AB=CD, AC=AC, а эти равенства выполняются (условие теоремы).

Нисходящий анализ.

1. Пусть ABCD – параллелограмм.

2. Тогда BC || AD и AB || DC.

3. Проведём диагональ АС, тогда получим: 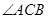= 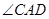, 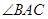= 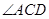(как накрест лежащие при параллельных прямых и секущей).

4. Из равенства накрест углов с учётом того, что АС – общая сторона следует равенство этих треугольников.

5. Тогда BC=DA, AB=CD, AC=AC, а эти равенства выполняются (условие теоремы).

Нетрудно теперь все рассуждения из нисходящего анализа провести в обратном порядке. В итоге получим синтетическое доказательство (результат поиска).

Чаще всего в школе учащимся предлагается именно синтетическое доказательство теорем, которое имеет ряд достоинств: исчерпывающая полнота, сжатость, краткость. Однако синтетический метод в методическом отношении имеет и свои недостатки. Остаётся неясным, как можно обнаружить такое доказательство, дополнительные построения никак не аргументируются. Учащиеся пассивно слушают и воспринимают такое доказательство, соглашаются с истинностью каждого умозаключения и не представляют, в каком направлении должны протекать дальнейшие рассуждения. Этот способ мало способствует самостоятельному открытию доказательства, и план рассуждений остаются скрытыми от учащихся.

В целом можно выделить 3 этапа работы над доказательством:

1. Подготовительный этап:

– повторение теорем (и их доказательств), связанных каким-либо образом с данной теоремой;

– выполнение практической работы, в ходе которой «открывается» метод доказательства теоремы;

– изучение и осмысление чертежа по содержанию теоремы;

– если возможно, разбиение теоремы на части или частные случаи и поиск доказательства отдельных частей;

– составление плана (схемы) доказательства (по необходимости).

2. Доказательство теоремы и её запись в соответствующей символике:

– доказательство ведётся поэтапно, все умозаключения логически обоснованы;

– доказательство теоремы кратко, сжато и записано в определённой символике.

3. Закрепление доказательства:

– обобщение метода доказательства и его основной идеи;

– выведение следствий из теоремы;

– на следующем уроке – доказательство при другом расположении чертежа;

– в домашней работе – превращение сокращённого книжного доказательства в развёрнутые цепочки умозаключений;

– доказательство теоремы другими методами (если это возможно);

– решение задач на доказательство с использованием данной теоремы и метода её доказательства;

– самостоятельное доказательство теорем, связанных с данной (обратной, противоположной, аналогичной).