Область действия кванторов. Свободные и связанные вхождения переменных в формулу. €

Введение в формальную логику

Учебное пособие

Для упражнений, помеченных знаком +, в конце даны ответы

Глава 4 [начало]

Классическая логика предикатов

Логика предикатов – логическая теория, в которой вводятся параметры трех типов для выражений естественного языка: для предикатных выражений, функторных и для логических имен. В классической логике предикатов продолжают действовать принцип двузначности классической логики высказываний: каждое высказывание принимает в точности одно из двух значений – истина (истинно) или ложь (ложно). Принцип функциональности работает для связок логики высказываний, но в логике предикатов вводятся две новые логические операции, которые не функциональны – кванторы: $ и ". В естественном языке символу $ – квантору существования – соответствуют выражения некоторый, какой-то, существует, найдется, какой-нибудь и т.п., а символу " – квантору общности – соответствуют выражения любой, всякий, произвольный, все, каждый и т.п.

Тема 1: Язык классической логики предикатов первого порядка

Основные понятия, которые необходимо усвоить: · логические и нелогические символы в ЯКЛП1 = · язык классической логики предикатов с символом равенства = (ЯКЛП1=) · логические и нелогические символы в ЯКЛП1 · правильно построенные выражения ЯКЛП1: терм и формула ЯКЛП1= · графы, соответствующие процедуре построения термов и формул ЯКЛП1= · область действия квантора · свободные и связанные переменные · предложение ЯКЛП1 = (замкнутая формула)

Алфавит ЯКЛП¹⁼ (перечень исходных символов)

I. Нелогические символы:

1. a, b, c, a₁, b₁, c₁, a₂… - индивидные (предметные) константы;

2. fⁿ, gⁿ, hⁿ, f₁ⁿ, g₁ⁿ, h₁ⁿ, f₂ⁿ,… - функциональные константы;

3. Pⁿ, Qⁿ, Rⁿ, Sⁿ, P₁ⁿ, Q₁ⁿ, R₁ⁿ, S₁ⁿ, P₂ⁿ … – предикатные константы;

4. x, y, z, x₁, y₁, z₁, x₂… - индивидные (предметные) константы.

II. Логические символы:

Ø, &, Ú, É, º, ^, Т, $, ", =.

III. Технические символы: левая и правая скобки и запятая: ( ) , .

Терм ЯКЛП¹:

1. всякая индивидная константа (a, b, c, a₁, b₁, c₁, a₂ и т.д.) есть терм;

2. всякая индивидная переменная (x, y, z, x₁, y₁, z₁, x₂ и т.д.) есть терм;

3. если Fⁿ есть какой-либо n-местный функциональный символ (fⁿ, gⁿ, hⁿ, f₁ⁿ, g₁ⁿ и т.д.) и о последовательностях символов t₁, t₂,…, t_n известно, что каждый из них есть терм, тогда термом также будет такая последовательность символов: Fⁿ(t₁, t₂,…, t_n).

4. терм есть последовательность символов, которая может быть построена по пп.1-4.

Примеры термов

1. b - по п.1

2. b₄₁₁ – по п.1

3. x₁ – по п.2

4. h¹(z) – по пп.2,3

5. h²(c,с) – по пп.1,3

6. h¹(h¹(z)) – по пп.2,3

7. f²(h¹(z),a) – по пп.1,2,3

8. f²(h¹(z), h²(y,z)) – по пп. 1,2,3

9. g³(h¹(h¹(а)), a, с) – по пп.1,3

Определение терма носит чисто синтаксический характер: оно задает некоторый класс записей, составленных из символов алфавита нашего языка, но не аппелирует к возможным смыслам этих записей, т.е. сами записи, подпадающие под определение терма, рассматриваются просто как последовательности некоторых объектов. Но эта дефиниция вводилась, разумеется, для того, чтобы впоследствии связать с ней осмысленные выражения некоторого типа, а именно: задающие объекты. Покажем (в предварительном порядке), как записи, имеющие вид терма, определяют структуры имен и именных форм. Так, структуру h¹(h¹(а)) имеют выражения 6²², ÖÖ5, отец отца Сократа. А такую форму как f²(a,h¹(z)) имеют, например, выражения 5+z², 7-z³, p+Öy, 5×у⁴, 5×sinx.

Формула ЯКЛП¹⁼:

1. ^, Т – формулы;

2. если Рⁿ есть какой-либо n-местный предикатный символ (Pⁿ, Qⁿ, Rⁿ, Sⁿ, P₁ⁿ и т.д.), а t₁, t₂,…, t_n – термы, тогда последовательность символов

Рⁿ( t₁, t₂,…, t_n) является формулой;

3. если t₁, t₂ – термы, тогда последовательность t₁=t₂ есть формула;

4. если А – формула, тогда ØА тоже формула;

5. если А и В – формулы, тогда (А&В), (АÚВ), (АÉВ), (АºВ) – формулы;

6. если К – квантор ($ или "), a - индивидная переменная и А – формула, тогда следующая последовательность также является формулой: КaА;

7. формулой является последовательность символов, которая может быть построена по пп.1-7.

Самые простые (в смысле построения) формулы назовем атомарными. Атомарная (элементарная) формула – формула, построенная по каким-то из пунктов 1-3.

Формулы, процедура построения которых включает хотя бы один из пп.3-6 назовем составными (сложными, молекулярными).

Вместо Ø t₁=t₂ будем писать t₁¹t₂.

Примеры атомарных формул

^

P¹(a) (читается «Р от а»; подразумевается объект а обладает свойством Р)

P¹(x)

P¹(f¹(а)) (читается «Р от f от а»; подразумевается объект, сопоставленный объекту а функцией f, обладает свойством Р)

R²(x,a) (читается «R от х, а»; подразумевается свойство находится в отношении R с объектом а)

R²(y,y)

R²(y₁₁,y)

R³(f¹(c), f¹(a), a)

R³(f¹(c), f¹(a), h²(y,z))

a=b

f¹(a)= h¹(h¹(с))

f¹(a)= h¹(g²(y,z))

Примеры термов и формул

Примеры составных формул

$xP(x)

$x(P(x)&Q(x)) (главный знак - $)

$xP(x)&Q(x) (главный знак - &)

"y"zQ(z,f¹(y)) (главный знак – квантор "y )

Ø"y"zQ(z,y) (главный знак - Ø)

"x$yR(x,y)Ú"y"zQ(z,y) (главный знак - Ú)

"x($yR(x,y)Ú"zQ(z,x)) (главный знак - квантор "x)

ØR(x,y)ÚQ(z,x) (главный знак - Ú)

Ø (a=b Ú c=b) Éa ¹b (главный знак - É)

Примеры неправильно построенных выражений (не термы и не формулы)

1. х&у. Ошибка: х и у – термы, а связка & (так же, как Ú, É, º), могут связывать только формулы.

2. f¹(Q¹(a)). Ошибка: после одноместного функционального символа (f¹) должен стоять один терм, а в нашем случае в скобках стоит формула - Q¹(a).

3. Øх & Øу. В этой записи два неправильно построенных выражения – Øх, Øу – соединены конъюнкцией. Øх – неосмысленная запись, поскольку в нашем языке отрицание может относится к структуре предложения (формуле), а не к терму (х - терм). То же с Øу.

4. P²(Q¹(a),S¹(a)). Ошибка: после символа двухместного предиката (P²) в скобках должны находиться два терма, а в нашей записи стоят две формулы (Q¹(a) и S¹(a)).

5. ∀x. Кванторы используются только при построении формулы, но в составе формулы в обязательном порядке должны присутствовать а) предикатные символы(Pⁿ, Qⁿ, Rⁿ, Sⁿ, P₁ⁿ и т.д.), либо б) выделенный предикатный символ равенства, либо в) логические константы (^, Т). В нашей записи их нет.

6. ∀x É ∃y. Слева и справа от импликации должны стоять формулы, а в примере 6 слева и справа от знака É стоят не формулы, а неправильно построенные выражения (см. предыдущий пример).

7. ∀xР¹(х) É ∃yР¹(∃х). Плохое место: Р¹(∃х). В скобках после одноместного предиката Р¹ должен стоять аналог имени – терм, а ∃х - не терм (в состав термов не входят кванторы). Если убрать из примера 7 символ квантора существования, тогда получим формулу ∀xР¹(х)É∃yР¹(х).

8. Р(а)=Р(с). Ошибка: символ равенства связывает термы, а в этом примере слева и справа от равенства стоят формулы.

9. $x"yR(x,y)ÉØ$y"аØR(x,а). Ошибка: запись "а невозможна, после квантора сразу должна идти переменная (x, y, z, x₁, y₁, z₁, x₂ и т.д.), а не константа (а – индивидная константа)[2].

10. Ø$y"ØR(x,у). Ошибка: после квантора общности (") нет переменной.

Упражнения

1. Что соответствует в естественном языке терму ЯЛП? Что формуле?

2.Определите, являются ли следующие последовательности символов осмысленными (правильно построенными) выражениями ЯЛП¹ (то есть термами или формулами). Там, где не указана местность функтора или предиката, считайте, что она та, которая и требуется записью (Например, в Р(х) Р – одноместный предикат, а в Р(а,у) - двухместный).

1. ⁺ xy

2. ⁺ (x,y)

3. ⁺ P²(x&y)

4. ⁺ Øа

5. ⁺ h³(g¹(f²(a,b)))

6. ⁺ ∀x(R(x)⊃∃y(P(y)&Q(x,y)))

7. a

8. x

9. f²(x,x)

10. x₁₈₂₄

11. f²(h²(a,b))

12. h¹(f²(a, h¹(z)))

13. f²h¹(a)

14. f¹(P¹(a))

15. f¹(a)& f¹(c)

16. P(z₁)

17. $P(x)

18. P(x,х)

19. "х f¹(x)

20. "х f¹(x)=h¹(h¹(x))

21. "aP(a)

22. P(a)

23. y¹(x)

24. Q²

25. Q¹("х)

26. ØR(x,y)

27. $xP(a)

28. Ø"xØ"y R(x,y)

29. $y(Q¹ É Р¹)

30. P¹(Q¹(a))

31. Ø $x"yÉ "хØ$y

32. $x"yR(x,y)ÉØ$y"xØR(x,y)

3. Укажите граф, соответствующий процедуре построения данного терма / формулы.

а) g(a, f(b))

б) Ø$x "y R(x,y) É"х$уØR(x,y)

в) $x(R(x) & "у(ØR(x,y)Ú ØR(x,y))

4. Укажите логические и нелогические константы, входящие в состав данных формул.

(а) P (x,c)

(б) "x P (x,c)

(в) "x P (x,c)É^

(г) Ø (Т º (∀x∃y((R(x) & R(y)) É Q(x,y)))

(д) $x("yQ(b,c,y) º R(x,y))Ú("z (Q (z) º R(z,b)))

Область действия кванторов. Свободные и связанные вхождения переменных в формулу. – см. лекцию

5. Укажите область действия каждого квантора в следующих формулах.

(а) "x P (x,c) ÉR(x)

(б) "x (P (x,c) ÉR(x))

(в) $x("yQ(y)ÉR(x,y))Ú("zQ(z)ÚR(z,x))

(г)⁺"x(P(x,y₁)º$yQ(y,x))&"z(R(x,y)ºR₁(y, x))

Зачем различать свободные и связанные вхождения переменных в формулу? Свободные вхождения переменных можно заменять на имена объектов, а для связанных вхождений такая замена – незаконна, бессмысленна. Пример Рассмотрим два выражения (записанные в прикладном языке арифметики) (1) x+y=7 (2) $х$у x+y=7.   Выражение (1) ни истинно, ни ложно. Все зависит от того, что мы припишем в качестве значений переменным х и у (какими числами их заменим, точнее – именами каких чисел). Выражение (2) уже есть (истинное) предложение (оно утверждает, что есть такие 2 (допустим, натуральных) числа, сумма которых есть число 7). Замена переменных на имена конкретных объектов в этом случае бессмысленна.

6. Определить, какие вхождения переменных являются свободными, а какие связанными в следующих формулах:

а. "x P (x,c)

б."x (P(x)ÉQ(y))

в. $x("yQ(y)ÉR(x,y))Ú("z Q (z)ÚR(z,x))

г. "x(P(x,y)É$yQ(y,z,x))

д.⁺ "x(P(x,y)ºQ(y,x))&"z(R(x,y)ºR₁(y, x))

е.⁺$x(P(x)ºQ(y))

ж.⁺ "x$y(P(x,y)ºQ(y,x))&"x"y(R(x,y)ºR₁(y, x))

Формула ЯКЛП называется замкнутой или предложением, е.т.е. она не содержит свободных переменных.

Термин предложение употребляется, таким образом, в двух смыслах: предложение естественного языка и предложение (формального) языка логики предикатов (= формула без свободных переменных)

7. Какие из следующих формул являются предложениями ЯКЛП?

a. P¹(x)

b. P¹(a)

c. $xP¹(x)

d. Q²(c,y)

e. Q³(a₂,a₂,c)

f. $x(P¹(x)& Q²(c,y))

g. $y(P¹(y)& Q²(c,y))É ($yR¹(y)& Q²(c,y))

h. "x"x₄"y((R(x₄)& R(x)& R(y))ÉØQ³(x,y,x₄))

i. "x"x₄"y(R(x₄)& R(x)& R(y))ÉØQ³(x,y,x₄)

j.⁺ $z"x(R²(x,z)ºQ²(x,x))ÉØQ³(x,z,z)

Договоренность Пусть a1, a2,…,an – какие-то предметные переменные (х, х1, у, у2, у1 и т.п.) и А – какая-то формула. Вместо "a1"a2…"an А будем писать "a1, a2,…, an А. Вместо $a1$a2…$an А будем писать $a1, a2,…, an А. Например, вместо "x"x4"y (Р(x,y) Ú S(х4,у) É Q(х,х4)) будем писать "x,x4,y(Р(x,y) Ú S(х4,у) É Q(х,х4)).

Ответы

Гл.4 Упр.3

1) Неосмысленная запись: ни терм, ни формула. Раз нет предикатных знаков, значит это либо терм, либо неправильная (неосмысленная) запись. Две переменные, записанные подряд не являются осмысленной записью.

2) Неосмысленная запись: ни терм, ни формула. Раз нет предикатных знаков, значит это либо терм, либо неправильная (неосмысленная) запись. Две переменные, записанные через запятую и взятые в скобки, не являются термом.

3) Неосмысленная запись: ни терм, ни формула. Раз в состав записи входит предикатный символ, то она является либо формулой, либо неправильно построена. Ошибка в данной записи: два терма
(x и y) соединены пропозициональной связкой &, которая может связывать, согласно определениям терма и формулы, только формулы.

4) Неосмысленная запись: ни терм, ни формула. Ошибка: нельзя отрицать термы (индивидная константа а – терм).

5) Терм.

6) Формула. Ее нагруженное дерево:

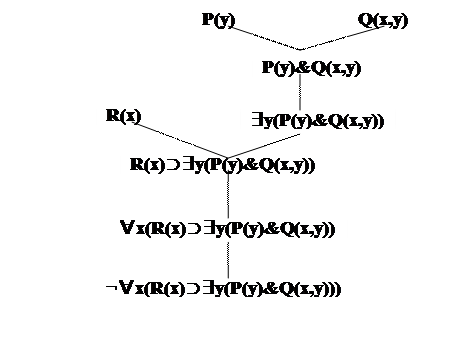
Гл.4 Упр.5(г)

Область действия квантора "x (подчеркнута):

"x (P(x,y₁)º$yQ(y,x)) & "z(R(x,y)ºR₁(y, x))

Область действия квантора $у (подчеркнута):

"x(P(x,y₁)º$yQ(y,x))&"z(R(x,y)ºR₁(y, x))

Область действия квантора "z (подчеркнута):

"x(P(x,y₁)º$yQ(y,x))&"z(R(x,y)ºR₁(y, x))

Гл.4 Упр.6

Свободные вхождения выделены жирным шрифтом и подчеркнуты, остальные вхождения переменных – связанные.

д."x(P(x,y)ºQ(y,x))&"z(R(x,y)ºR₁(y,x))

е. $x(P(x)ºQ(y))

ж. свободных вхождений переменных нет

Гл.4 Упр.7(j) Не предложение, формула содержит свободные вхождения переменных (они подчеркнуты):

$z"x(R²(x,z)ºQ²(x,x))ÉØQ³(x,z,z)

[1] Граф набран Т.В.Сальниковой; задание, взятое из книги Р.Столл «Множества. Логика. Аксиоматические теории» М., 1968, помечено [Ст], а из учебника Н.Н.Непейводы «Прикладная логика» - [Н].

[2] Выражения с постоянным значением бессмысленно квантифицировать (ставить перед ними кванторные слова: все, любой, некоторый, существует, есть, какой-нибудь и т.д.). Ср., например, выражения для любой РФ верно, что… или есть такие Соединенные Штаты Америки, в которых… Очевидно, что употребление слов любой и есть в этих фразах бессмысленно.