Вычисление суммы. Рекуррентные формулы.

Условие задачи: Для x, изменяющегося в интервале от x0 до xk с шагом h, вычислить значения бесконечной суммы y(x) с точностью e=0.00001.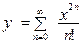

e = 0.000001: n = 1

For x = xh To xk Step dx

y = 0: i = 0: u = 1

While Abs(u) > e : y = y + u : u = (x) ^ 2 / (i + 1) * u : i = i + 1

Wend : n = n + 1

Next x

Вычисление чисел Фибоначчи.

Sub Fib1()

ActiveCell.FormulaR1C1 = "1"

Range("A2").Select

ActiveCell.FormulaR1C1 = "2"

Range("A3").Select

ActiveCell.FormulaR1C1 = "=R[-2]C+R[-1]C"

Range("A3").Select

Selection.AutoFill Destination:=Range("A3:A20"), Type:=xlFillDefault: Range("A3:A20").Select

18. Нахождение «сигнальной» матрицы В = sign(A).

Sub matAB()

Dim a(3, 3) As Integer : Dim b(3, 3) As Integer

Dim i, j As Integer : Dim s1, s2 As String

For i = 1 To 3 : For j = 1 To 3

If a(i, j) > 0 Then: b(i, j) = 1: Else

If a(i, j) = 0 Then: b(i, j) = 0: Else: b(i, j) = -1: End If

End If: Range(s1).Cells = b(i, j): Next: Next: End Sub

19. Решение уравнений вида f(x) = 0. Метод Ньютона.

При x=а f’(x)*f ’’(x)<0 – функция убывающая и f’(x)*f ’’(x)>0-функция возрастающая.

Расчетная формула Ньютона имеет вид:

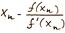
Вычисления ведутся до тех пор, пока |x_n-x_n-1|<E

While Abs(f(x)) > 0.01

i = i + 1

x = x - f(x) / f1(x)

Wend

End Sub

20. Решение уравнений вида f(x) = 0. Метод деления отрезка пополам.

Алгоритм:

1. Ввести данные (а, b, е)

2. Если нужная точность достигнута (|b-a|<2е), переходим у пункту6

3. Взять середину очередного отрезка c=(a+b)/2

4. Если значение функции в точках а и с одного знака (f(а)*f (с)>0), то в качестве следующего отрезка взять другую половину а=с, иначе b=c.

5. Перейти к пункту 2

6. Напечатать ответ (a+b)/2

x = Del(a, b, eps)

Function Del(a As Double, b As Double, e As Double) As Double

Dim x As Double, n As Integer

If fun(a) * fun(b) <= 0 Then

n = 0: While (b - a) > e: n = n + 1 : x = (a + b) / 2

If fun(a) * fun(x) <= 0 Then

b = x: Else: a = x: End If

Range("B5").Cells = n : Del = (a + b) * 0.5

Wend: Else: MsgBox ("a,b=?")

Exit Function : End If : End Function

21. Решение уравнений вида f(x) = 0. Метод хорд.

Xn+1= Xn-(f(Xn)(b- Xn))/(f(b)-f(Xn))

Xn+1= Xn-(f(Xn)(Xn-а))/(f(Xn)-f(a))

| Xn+1- Xn|<Ɛ

x = Hor(a0, b0, eps)

Function Hor(a As Double, b As Double, e As Double) As Double: Dim x As Double, x0 As Double, n As Integer: If fun(a) * fun(b) <= 0 Then

n = 0: x0 = a: x = b: While Abs(x0 - x) > e

n = n + 1: x0 = x: x = b - fun(b) * (b - a) / (fun(b) - fun(a)): If fun(a) * fun(x) <= 0 Then: b = x : Else : a = x: End If : Hor = x: Wend : Else MsgBox ("a,b=?"): Exit Function : End If : End Function

22. Решение систем линейных уравнений итерационнымиметодами. Метод простой итерации.

Нормой вектора B и матрицы А называют соответственно следующие числа: ;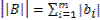

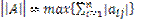
количество итераций m: m≥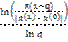

|x^(m)- x^(m-1)| ≤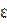

X_n+1= X_n-(f(X_n)(b- X_n))/(f(b)-f(X_n))

X_n+1= X_n-(f(X_n)(X_n-а))/(f(X_n)-f(a))

|X_n+1-X_n|<Е

Алгоритм:

1) Преобразуем исходную систему к виду x=αx+β.

2) Находим норму матрицы.

3) Если |α| < 1, то переходим к пункту 4.

4) Задается начальное приближение и ε

5) Рассчитывается количество итераций i.

6) Вычисляется очередная итерация x_i+1=n(x_i)

7) Если |x^(m)- x^(m-1)| ≤ 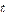, то процесс закончен, иначе переход к пункту 6.

x = Hor(a0, b0, eps)

Call Iter(eps, x, n)

For i = 1 To 4

x(i) = 0: Next i: n = 0

Do : n = n + 1: l = False

For i = 1 To 4 : x0(i) = x(i) : Next i

For i = 1 To 4 : x(i) = b(i) / a(i, i)

For j = 1 To i – 1 : x(i) = x(i) - a(i, j) / a(i, i) * x0(j) : Next j

For j = i + 1 To 4 : x(i) = x(i) - a(i, j) / a(i, i) * x0(j) : Next j

If Abs(x(i) - x0(i)) > e Then : l = True

End If : Next i : Loop Until Not l : End Sub