Примеры применения генетических алгоритмов в задачах управления
Рассмотрим применение ГА в задачах интеллектуального управления.
Пример 1. Применение ГА для оптимального выбора нечетких правил.
Задача 1 – парковка движущегося объекта.
Рассмотрим следующую задачу управления движением тележки (рис.2.29): разработать нечеткий регулятор (НР), который переводит тележку (объект управления - ОУ) из заданных начального положения и начальной скорости в целевое положение (0,0) (центровка и останов) за минимальное время.
Начальное состояние ОУ: 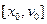 ; Целевое (конечное) состояние ОУ: [0,0].
; Целевое (конечное) состояние ОУ: [0,0].

Рис. 2.29. Задача парковки движущегося объекта
Математическая модель для заданной задачи управления представляется следующими уравнениями движения:
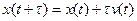
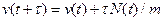 ,
,
где 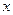 – положение тележки на дороге, представленной одномерной осью
– положение тележки на дороге, представленной одномерной осью 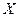 в модели объекта на рис.2.29;
в модели объекта на рис.2.29; 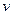 – скорость движения тележки;
– скорость движения тележки; 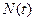 – сила управления, приложенная к тележке;
– сила управления, приложенная к тележке; 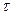 – шаг управления, m – масса тележки.
– шаг управления, m – масса тележки.
Прежде всего, вспомним, какие шаги должны быть сделаны при построении НР:
· описание входных и выходных переменных и их множеств значений (Таблица 2.5а);
· разбиение множеств значений на подмножества значений;
· описание этих подмножеств с помощью нечетких множеств с заданными функциями принадлежности (рис.2.30);
· построение множества нечетких правил (Таблица 2.5б).
Итак, на вход НР поступают значения следующих переменных:
· 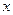 – положение тележки;
– положение тележки;
· 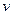 – скорость движения тележки.
– скорость движения тележки.
На выходе – значения силы управления 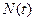 , приложенной к тележке.
, приложенной к тележке.
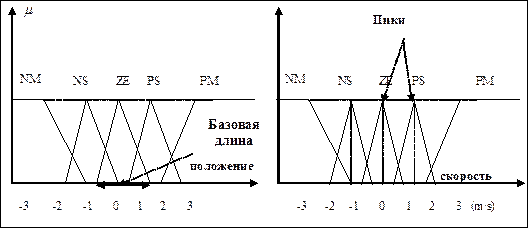
Рис. 2.30. Функции принадлежности
Пространство изменения переменных 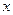 ,
, 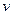 и
и 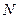 будем описывать с помощью следующих лингвистических переменных {NM, NS, ZE, PS, PM} = {«negative medium», «negative small», «Zero», «positive small», «positive medium»}.
будем описывать с помощью следующих лингвистических переменных {NM, NS, ZE, PS, PM} = {«negative medium», «negative small», «Zero», «positive small», «positive medium»}.
Будем рассматривать следующие нечеткие правила:
ЕСЛИ 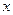 есть {NM,…, PM} И v есть {NM,…, PM}
есть {NM,…, PM} И v есть {NM,…, PM}
ТО 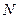 есть {NM, NS, ZE, PS, PM}.
есть {NM, NS, ZE, PS, PM}.
Приведенный тип правил соответствует модели нечеткого вывода Мамдани.
В общем виде правила в такой модели выглядят следующим образом:
Правило l: ЕСЛИ 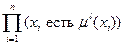 ТО
ТО 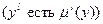 ,
,
где 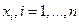 – входные лингвистические переменные, «
– входные лингвистические переменные, « 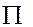 » операция нечеткой конъюнкции.
» операция нечеткой конъюнкции.
В общем виде выходное значение в модели Мамдани (с нечеткой конъюнкцией в виде умножения, синглетон-фаззификатором и дефаззификатором «средний максимум») вычисляется по следующей формуле:
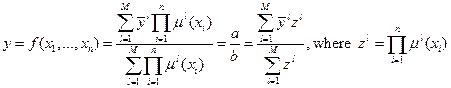 ,
,
где 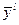 - точка максимального значения (центра) функции
- точка максимального значения (центра) функции 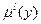 .
.
Различные НР имеют различные функции принадлежности и различные множества нечетких правил.
Нашей задачей является найти оптимальное множество нечетких правил так, чтобы НР осуществлял задачу управления за минимальное время.
Первый шаг в применении ГА – выбор способа кодирования потенциальных решений.
Что такое «потенциальные решения» для нашей задачи? Это множество нечетких правил (НП), которое может быть представлено в виде так называемой таблицы «look-up-table», показанной в Таблице 2.5 б.
Введем следующее кодирование для типа функций принадлежности (лингвистических переменных) внутри Таблицы 2.5:
1 - NM, 2 - NS, 3 - ZE, 4 - PS, 5 - PM.
| Таблица 2.5 а Параметры модели | Таблица 2.5 б Множество НП |
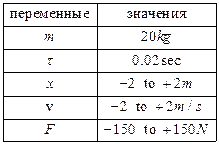 | 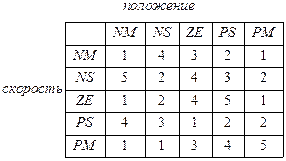 |
Выставив все значения строк таблицы в одну строку, получим строку из 25 позиций - {1432152432124514312211345}, которую легко перевести в бинарную строку, которая и будет служить хромосомой для данной задачи оптимизации с помощью ГА. Зададим также важные параметры ГА поиска: размер популяции = 100; максимальное число генераций = 100; вероятность скрещивания = 0.7; вероятность мутации = 0.03.
В качестве оператора селекции используется разновидность метода «tournament selection»: две или более хромосомы выбираются случайным образом и их значения пригодности сравниваются. Хромосомы с большими значениями пригодности копируются в следующую генерацию. Для лучшего поиска решения, ГА процесс разделяется на две стадии: стадия 1, называемая «эволюцией», и стадия 2, называемая «refinement stage». На первой стадии ГА ищет приемлемые решения по управлению такие, что ошибка управления минимальна (заданное значение). На второй стадии отбираются решения с минимальным временем, переводящим состояние ОУ из положения 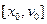 в целевое положение [0,0]. Опишем стадию 1.
в целевое положение [0,0]. Опишем стадию 1.
Стадия 1.
Число генераций равно 30. Функция пригодности (ФП) «награждает» каждое решение в зависимости от того, как близко данное решение к заданному пределу ошибки управления = 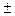 0.5 по
0.5 по 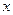 и по
и по 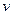 .
.
Введем функцию пригодности ГА для оценки пригодности текущей хромосомы, представляющей собой множество нечетких правил, т.е. некоторый НР. Для вычисления 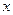 и
и 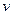 используется математическая модель.
используется математическая модель.
Функция пригодности для стадии 1 (эволюции):
(if ( 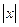 < 0.5 ) and (
< 0.5 ) and ( 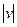 < 0.5) then fitness =
< 0.5) then fitness = 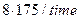
%{ 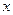 и
и 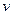 в пределах значений ошибки управления}
в пределах значений ошибки управления}
else ( if ( 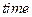 = 175 ) then
= 175 ) then
%{максимальное число шагов управления задачи}
(if ( 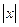 < 1.0 ) and (
< 1.0 ) and ( 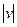 < 1.0) then fitness =
< 1.0) then fitness = 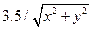 else fitness =
else fitness = 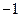 )
)
if ( ( 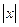 > 5.0 ) and (
> 5.0 ) and ( 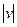 > 5.0 ) then fitness =
> 5.0 ) then fitness = 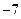 ).
).
Примечание: За символом «%» идет комментарий.
Обсудим данную функцию. Если хромосома успешна по критерию качества управления, то она оценивается в зависимости от времени, необходимого для выполнения задачи управления. Минимальное значение ФП в этом случае равно 8 (так как 175 – заданный лимит шагов управления).
Если хромосома выходит за рамки «175 шагов», то она или «поощряется» положительным значением ФП (если удовлетворительное качество управления ( 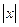 < 1.0 ) и (
< 1.0 ) и ( 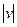 < 1.0) или «наказывается» отрицательным значением ФП, если плохое качество управления. Если хромосома неуспешна по критерию качества управления (
< 1.0) или «наказывается» отрицательным значением ФП, если плохое качество управления. Если хромосома неуспешна по критерию качества управления ( 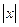 > 5.0 ) и (
> 5.0 ) и ( 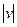 > 5.0), то она наказывается большим отрицательным значением ФП.
> 5.0), то она наказывается большим отрицательным значением ФП.
Рисунки внизу 2.31 и 2.32 иллюстрируют структуру хромосомы и процесс вычисления функции пригодности.

Рис. 2.31. Иллюстрация процесса декодирования хромосомы
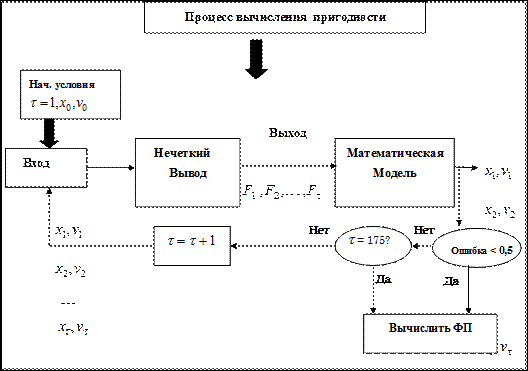
Рис. 2.32. Схема вычисления функции пригодности
Стадия 2.
Число генераций - от 31 -ой до 100-ой.
Функция пригодности для стадии 2 (отбора по критерию времени):
(if ( 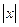 < 0.5 ) and (
< 0.5 ) and ( 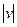 < 0.5)
< 0.5)
%{ 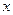 и
и 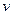 в пределах значений ошибки управления}
в пределах значений ошибки управления}
then fitness = 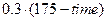
else (if ( 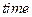 = 175 ) % {максимальное число шагов управления задачи}
= 175 ) % {максимальное число шагов управления задачи}
then fitness = 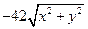 ))
))
if (( 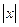 > 5.0 ) and (
> 5.0 ) and ( 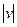 > 5.0 ) then fitness =
> 5.0 ) then fitness = 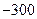 ).
).
На рис. 2.33 показан результат ГА оптимизации для задачи 1.
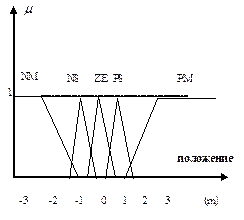 (a) (a) | 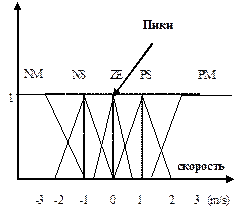 (b) (b) |
Рис. 2.33. НР с оптимально выбранным множеством НП
Множество НП 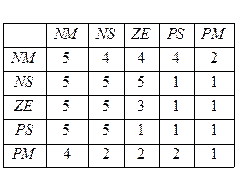 (c) (c) | 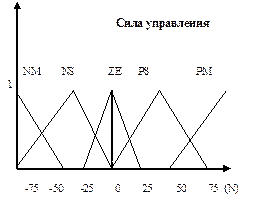 (d) (d) |
Рис. 2.33. НР с оптимально выбранным множеством НП
Примечание. На рис.2.33 значения (а), (b) и (d) фиксированы, значения (c) найдены с помощью ГА.
Пример 2. Рассмотрим следующую задачу: с помощью оптимизации, основанной на ГА, выбрать такие коэффициенты усиления ПИД регулятора 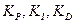 , чтобы ошибка управления была минимальной (основной критерий качества управления).
, чтобы ошибка управления была минимальной (основной критерий качества управления).
Общая схема оптимизации коэффициентов усиления ПИД регулятора с помощью ГА показана на рис. 2.34.
Примечание. В этом примере мы рассматриваем общие вопросы поставленной задачи без уточнения ОУ и цели управления.
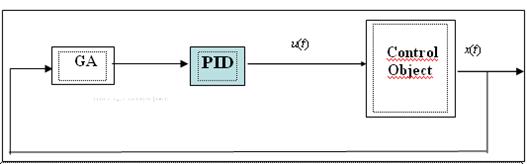
Рис. 2.34. Схема оптимизации с помощью ГА коэффициентов усиления ПИД регулятора
Рассмотрим два варианта этой задачи: 1) поиск оптимальных постоянных коэффициентов усиления ПИД регулятора; и 2) поиск оптимальных переменных коэффициентов усиления ПИД регулятора, которые используются в нечетких регуляторах;
Поскольку целью управления (в общем виде) является минимизация ошибки управления, то в качестве функции пригодности можно выбрать, например, следующую функцию:
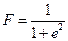 , где
, где 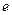 - ошибка управления.
- ошибка управления.
Ошибка управления (по определению) вычисляется как
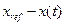 ,
,
где 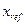 - задающий сигнал (цель управления), а
- задающий сигнал (цель управления), а 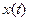 - состояние ОУ.
- состояние ОУ.
Тогда, отыскивая с помощью ГА максимум функции 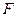 , мы тем самым минимизируем ошибку управления
, мы тем самым минимизируем ошибку управления 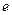 . В этом случае большие значения функции пригодности будут соответствовать малым значениям ошибки управления, а, следовательно, лучшему качеству управления ПИД регулятора.
. В этом случае большие значения функции пригодности будут соответствовать малым значениям ошибки управления, а, следовательно, лучшему качеству управления ПИД регулятора.
Так как ГА работает с закодированными параметрами, обсудим способ кодирования для нашей задачи.
Вначале рассмотрим простейший случай – задача оптимизации постоянных коэффициентов усиления ПИД регулятора - 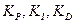 .
.
Задача 2: поиск оптимальных постоянных коэффициентов усиления ПИД регулятора. Без потери общности, предположим, что необходимо 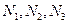 бит для кодирования значений ПИД параметров(
бит для кодирования значений ПИД параметров( 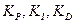 ). В этом случае, размер хромосомы
). В этом случае, размер хромосомы 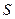 , представляющей значения
, представляющей значения 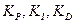 , будет
, будет 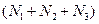 бит. Представим
бит. Представим 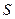 как S =
как S = 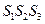 , где
, где 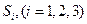 - следующие строки:
- следующие строки:
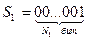 ,
, 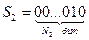 , и
, и 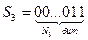 .
.
Рассмотрим, как определить число 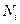 бит для кодирования ПИД параметров. Допустим, что
бит для кодирования ПИД параметров. Допустим, что
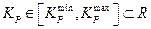 ,
, 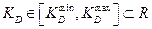 ,
, 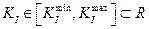 ,
,
где R есть множество всех действительных чисел.
Для каждого интервала 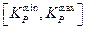 построим соответствующую решетку значений следующим образом. Зададим расстояние
построим соответствующую решетку значений следующим образом. Зададим расстояние 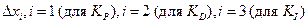 между соседними точками решетки. Это расстояние называется шагом дискретизации ГА (GA discretization step). Тогда общее число точек
между соседними точками решетки. Это расстояние называется шагом дискретизации ГА (GA discretization step). Тогда общее число точек 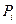 в решетке будет вычисляться по формуле:
в решетке будет вычисляться по формуле:
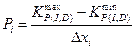 .
.
Для выбора лучшего значения (с точки заданной функции пригодности), например, для 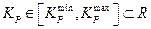 ГА исследует все точки в решетке:
ГА исследует все точки в решетке:
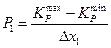
Длина бинарной хромосомы 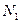 для кодирования десятичного числа из
для кодирования десятичного числа из 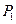 определяется по формуле:
определяется по формуле:
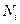 =
= 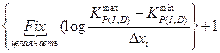 .
.
Примечание. Для вычисления значений пригодности хромосомы, бинарные значения 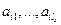 преобразуются обратно в десятичные числа по следующей формуле:
преобразуются обратно в десятичные числа по следующей формуле:
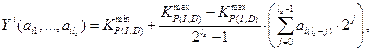
где 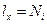 (
( 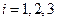 ).
).
Графическая иллюстрация этих вычислений приведена на рис. 2.34.
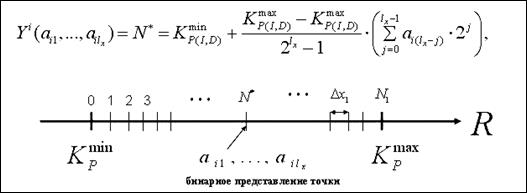
Рис. 2.34. Вычисление значений бинарных хромосом
После того, как кодирование ПИД параметров, функция пригодности и пространство поиска для коэффициентов усиления ПИД регулятора определены, можно применять стандартный ГА.
На рисунке 2.35 показана Матлаб–Симулинк структура системы моделирования оптимальных коэффициентов усиления ПИД- регулятора.
Задача 3: поиск оптимальных переменных коэффициентов усиления ПИД регулятора для нечеткого регулятора
В этом случае мы имеем дело с коэффициентами усиления ПИД регулятора, зависящими от времени. 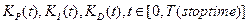 .
.
Для реализации этой задачи разработана система, названная SSCQ - система моделирования качества управления (от англ. simulation system of control quality). Матлаб–Симулинк структура системы SSCQ показана на рис.2.36.
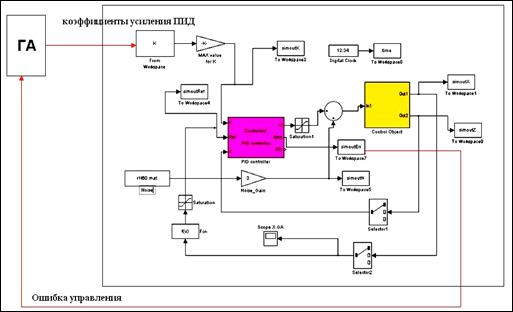
Рис. 2.35. Матлаб/Симулинк структура системы моделирования оптимальных коэффициентов усиления ПИД-регулятора.
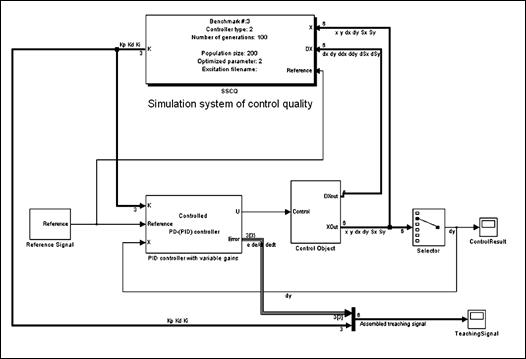
Рис. 2.36. Матлаб/Симулинк структура системы оптимизации управления, основанной на ГА
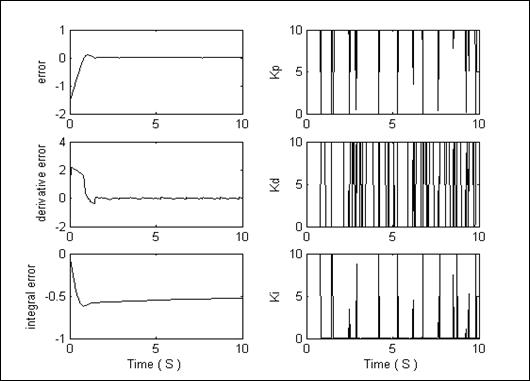
Рис. 2.37. Пример обучающего сигнала
С помощью ГА находим оптимальные значения коэффициентов усиления ПИД 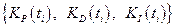 для моментов времени
для моментов времени 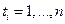 . В дальнейшем эти значения будем называть законами управления. Объединяя законы управления с соответствующими значениями ошибки управления (control error), ее скорости (derivative of error) и интегральной части (integral error), получаем так называемый обучающий сигнал (ОС) (teaching signal (TS)).
. В дальнейшем эти значения будем называть законами управления. Объединяя законы управления с соответствующими значениями ошибки управления (control error), ее скорости (derivative of error) и интегральной части (integral error), получаем так называемый обучающий сигнал (ОС) (teaching signal (TS)). Пример ОС показан на рис. 2.37.
Данный обучающий сигнал используется на этапе обучения в нечеткой нейронной сети (ННС) (Fuzzy Neural Network (FNN)), реализующей модель нечеткого вывода Сугено нулевого порядка.
Теория ННС является одной из составляющих компонент технологии мягких вычислений. В следующем параграфе мы обсудим основные понятия ННС и алгоритмы их обучения.
2.4. Искусственные и нечеткие нейронные сети: основные понятия и применение
В данной главе мы обсудим основные понятия в теории искусственных нейронных сетей (Artificial neural networks), рассмотрим обобщение на нечеткие нейронные сети и их применение.
Искусственные нейронные сетипредставляют собой математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма.
Широкое распространение ИНС связано с их следующими двумя ключевыми характеристиками:
1) адаптивными свойствами, позволяющими «обучаться на примерах» (подробнее смотри далее);
2) структура ИНС воплощает свойство параллелизма вычислений, что позволяет находить решения в реальном времени.
Эти свойства ИНС позволяют использовать их для решения следующих проблем:
· аппроксимация функций на основе ряда данных;
· распознавание образов;
· кластеризация и классификация данных;
· обучение в области статистической обработки данных;
· накопление знаний через обучение на примерах;
· предсказание и прогноз;
· оптимизация;
· ассоциативная память;
· нелинейное моделирование и управление.
Понятие искусственной нейронной сети (ИНС) возникло при изучении процессов, протекающих в коре головного мозга, и при попытке смоделировать эти процессы. Сети называются «нейронными» благодаря аналогии с нейрофизиологией, наукой о человеческом мозге и его нервной системе. Известно, что наш мозг содержит порядка 1011 нейронов и имеет порядка 1015 связей между нейронами. Это очень большие числа. Для сравнения, такое же количество звезд в нашей галактике «Млечный Путь». Наличие такого количества взаимосвязей определяет высокий уровень параллелизма в процессах обработки информации и высокую скорость реакции (нахождения решения) нашего мозга. Мозг человека – сложная вычислительная система, состоящая из нейронов различного типа (по форме и функциям). Одна из базовых особенностей нашего мозга является – способность к обучению. Моделирование этой способности является также одной из основных целей в исследованиях по разработке теории (моделей) ИНС.
История ИНС исследований восходит к работам McCuloch и Pitts (1943), Hebb (1949), Rosenblatt (1958,1961), Rochester (1956), Widrow (1960), и продолжена в работах Kohonen (1972), Hopfiled (1982), Cohen и Grossberg (1983) и др. Чтобы представить различные модели ИНС, рассмотрим вначале общую схему работы биологического нейрона.
