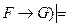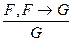Законы логики. Равносильные преобразования
1. Закон коммутативности
x  y
y  y
y 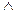 x; x
x; x 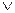 y
y 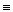 y
y 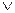 x
x
2. Закон ассоциативности
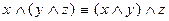 ;
; 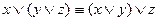
3. Закон дистрибутивности
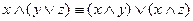 ;
; 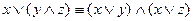
4. Закон Де Моргана
ù ( 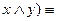 ù x
ù x 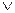 ù y ù (
ù y ù ( 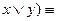 ù x
ù x 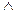 ù y
ù y
5. Закон поглощения
x 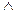 (x
(x 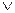 y)
y) 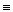 x x
x x 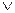 (x
(x 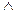 y)
y) 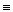 x
x
x 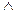 0
0 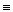 0 x
0 x 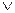 0
0 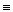 x
x
x 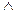 1
1 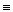 x x
x x 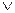 1
1 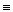 1
1
6. Закон исключения импликации
x 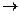 y
y 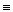 ù x
ù x 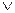 y
y
7. Закон исключения эквивалентности
x 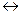 y
y 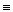 (x
(x 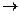 y)
y) 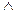 (y
(y 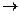 x)
x)
8. Закон исключения двойного отрицания
ù ù x 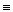 x
x
9. Закон идемпотентности
x 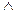 x
x 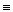 x x
x x 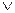 x
x 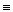 x
x
10. Закон исключения третьего
x 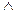 ùx
ùx 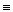 1 x
1 x 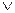 ù x
ù x 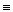 0
0
Логические следствия.
Определение: Пусть А1, А2,…Аm, В-формулы алгебры высказывания. Формула В-логическое следствие формул А1, А2,…Аm, если при любом наборе истинностных значений, входящих в неё пропозициональных переменных, формула В получает значение истина всякий раз, когда каждая из формул А1, А2,…Аm, получает значение истина.
A 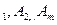
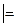 B
B
И говорят, что А1, А2…Аm влекут логически В.
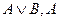
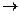 C, B
C, B 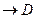
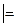 C
C 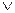 D
D
Запятую заменяют конъюнкцией, а логическое следствие - импликацией.
((A 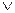 B)
B) 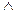 (A
(A 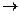 C)
C) 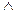 (B
(B 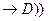
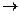 (C
(C 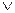 D)
D)
Правило вывода в алгебре высказываний.
Определение логического следствия А1, А2…Аm 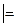 В, тесно связано с понятием тавтология: из А1, А2…Аm
В, тесно связано с понятием тавтология: из А1, А2…Аm 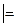 В тогда и только тогда, когда А1, А2…Аm
В тогда и только тогда, когда А1, А2…Аm 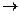 В является тавтологией.
В является тавтологией.
Очень часто формулы логического следствия записывают: А1, А2,…,Аm
В
Данную формулу называют правилом вывода формулы В из формул А1, A2…Аm.
Данное правило вывода означает : если истинными будут все формулы А1, А2…Аm, то и формула В является истинной. Правила вывода являются теми логическими средствами, с помощью которых мы из одних предложений строим умозаключения о справедливости других предложений.
Итак, всякая тавтология вида А 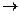 В определяет логическое следствие А
В определяет логическое следствие А 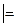 В и значит правило вывода
В и значит правило вывода 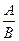
Рассмотрим примеры тавтологий и соответствующее им правило вывода:
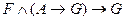
F, (